Дисперсионный анализ в медицине и здравоохранении.
1. Дисперсионным анализом называют группу статистических методов, разработанных английским математиком и генетиком Р. Фишером в 20-х годах ХХ-го века для ряда экспериментальных задач биологии и сельского хозяйства.
Постановка задачи. Пусть даны генеральные совокупности X1, X2,…, Xk., где:
- все «k» генеральных совокупностей распределены нормально;
- дисперсии всех генеральных совокупностей одинаковы.
При этих условиях и заданном уровне значимости «р» требуется проверить нулевую гипотезу о равенстве выборочных средних, т.е. H0: 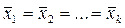 .
.
Каждая из генеральных совокупностей подвержена влиянию одного или нескольких факторов, которые могут изменять их средние значения.
Фактором называется показатель, который оказывает влияние на конечный результат.
Конкретную реализацию фактора называют уровнем фактора.
Значение измеряемого признака называют откликом на фактор.
Например, некоторое количество больных гипертонией разбиты случайным образом на «k» групп, каждой из которых назначен прием определенного лекарства. В результате контролируется среднее значение показателя изменения артериального давления.
В данном примере:
- значения показателя в «i»-ой группе, состоящей из «ni» больных – это «i»-я выборкаобъема «ni»;
- лекарство - это фактор, влияющий на величину контролируемого показателя;
- показатель изменения артериального давления - это отклик на воздействие фактора.
Предполагается, что по группам принимаемые лекарства различаются либо видом, либо дозой, либо еще каким-либо образом. Тогда воздействующий фактор подразделяется на некоторые составляющие, называемые уровнями фактора.
Если фактор оказывает воздействие на величину отклика, то нулевая гипотеза о равенстве средних H0: 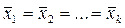 отвергается.
отвергается.
В зависимости от количества изучаемых факторов дисперсионный анализ делится на однофакторный и многофакторный.
В примере с изменением артериального давления можно исследовать:
· фактор времени года (уровни: зима, весна, лето, осень);
· фактор места эксперимента (уровни: лечение в стационаре или дома);
· фактор режима (уровни: постельный, обычный или регулярные пешие прогулки на свежем воздухе) и т.п.
Выборочные данные для однофакторного дисперсионного анализа оформляют в виде таблицы (таблица 4.1).
Таблица 4.1.
| Номер испытания | Уровень фактора А | |||
| A1 | A2 | … | Ak | |
| x11 | x12 | … | x1k | |
| x21 | x22 | … | x2k | |
| ... | … | … | … | … |
| r | 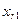
| 
| … | 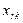
|
| Групповая средняя | 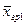
| 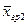
| … | 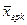
|
2. Основная цель дисперсионного анализа состоит в разбиении выборочной дисперсии на две компоненты:
- первая – это факторная дисперсия, она соответствует влиянию фактора на изменчивость средних значений;
- вторая – это остаточная дисперсия, она обусловлена случайными причинами и не влияет на изменчивость средних значений.
Для численной оценки влияния исследуемого фактора используют сравнение этих компонент с помощью F-критерия Фишера.
Факторная дисперсия ( 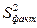 ) – это дисперсия, которая соответствует влиянию фактора на изменение средних значений выборки:
) – это дисперсия, которая соответствует влиянию фактора на изменение средних значений выборки:
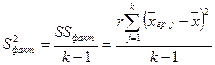 , (4.1)
, (4.1)
где  - факторная сумма квадратов отклонений, k - количество уровней фактора, r -количество значений в каждой группе,
- факторная сумма квадратов отклонений, k - количество уровней фактора, r -количество значений в каждой группе, 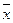 - общая средняя,
- общая средняя, 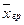 - групповая средняя.
- групповая средняя.
Остаточная дисперсия ( 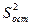 ) – это дисперсия, возникающая по случайными причинами и не влияющая на изменение средних значений выборки:
) – это дисперсия, возникающая по случайными причинами и не влияющая на изменение средних значений выборки:
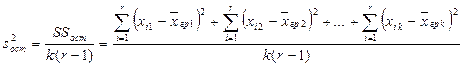 , (4.2)
, (4.2)
где 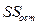 - остаточная сумма квадратов отклонений.
- остаточная сумма квадратов отклонений.
Общая дисперсия ( 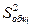 ) – это сумма факторной и остаточной дисперсий:
) – это сумма факторной и остаточной дисперсий:
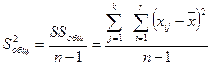 , (4.3)
, (4.3)
где 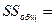
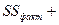
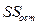 .
.
3. Схема применения однофакторного дисперсионного анализа:
1) Н0: 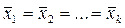 .
.
H1: 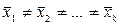 .
.
2) р=0,05- уровень значимости.
3) 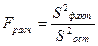 . (4.4)
. (4.4)
4) 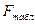 (р, f1, f2) ,
(р, f1, f2) ,
где f1=k-1, f2=k(r-1) – число степеней свободы (табличные значения), k - количество уровней фактора, r - количество значений в каждой группе.
5) Если 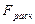 ≤
≤ 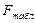 , то «H0» принимается.
, то «H0» принимается.
Если 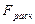 >
> 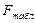 , то «H0» отвергается.
, то «H0» отвергается.
Пример 4.1. Среди взрослого населения определенной возрастной категории фиксировалось число заболеваний дыхательных путей за два года. Цель исследования – статистическое доказательство влияния курения на заболеваемость дыхательных путей.
Случайным образом были отобраны 3 группы по 4 человека каждая, из них: 1 группа - некурящие, 2 группа - стаж курильщика - до 5 лет, 3 группа - стаж курильщика более 5 лет.
Таким образом, исследуемый фактор «А» - курение, уровни фактора, А1, А2, А3 - стаж курильщика. Отклик на фактор курения - число заболеваний дыхательных путей.
Были получены 12 значений числа заболеваний – 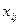 , где j - номер уровня фактора (j=1, 2, 3), i - номер элемента в соответствующей выборке (группе), i =1, 2, 3, 4:
, где j - номер уровня фактора (j=1, 2, 3), i - номер элемента в соответствующей выборке (группе), i =1, 2, 3, 4:
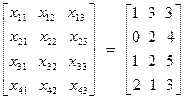 .
.
Предполагаем, что 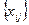 - выборка из нормальной генеральной совокупности.
- выборка из нормальной генеральной совокупности.
Все данные необходимо занести в таблицу:
| Номер испытания | Уровень фактора «А» | ||
| A1 | A2 | А3 | |
| Групповая средняя | 4/4=1 | 8/4=2 | 15/4=3,75 |
Решение.
1) Н0: 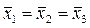 .
.
H1: 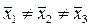 .
.
2) р=0,05- уровень значимости.
3) Вычисляется:
3.1) Общая средняя:
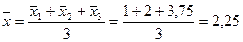 .
.
3.2) Факторная сумма квадратов отклонений:
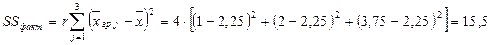 .
.
3.3) Остаточная сумма квадратов отклонений:
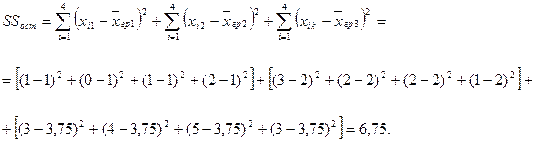
3.4) Факторная дисперсия
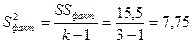 .
.
3.5) Остаточная дисперсия
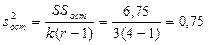 .
.
3.6) 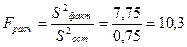 .
.
4) 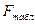 (0,05; 2; 9)=4,26.
(0,05; 2; 9)=4,26.
5) 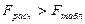 , то «H0» отвергается, значит фактор курения значимо влияет на заболеваемость дыхательных путей.
, то «H0» отвергается, значит фактор курения значимо влияет на заболеваемость дыхательных путей.
5. Литература:
1. Васильева Л.А. Статистические методы в биологии, медицине и сельском хозяйстве: Учеб. пособие для вузов. - Новосибирск, Новосибирский Государственный университет, 2007. - 128 с
2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. - 9-е изд., стер. - М.: Высш. шк., 2003. - 479 с.
3. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
4. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах / Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
5. Основы высшей математики и математической статистики: Учебник / И.В. Павлушкин и соавт. - М.: ГЭОТАР-МЕД, 2004. - 424 с.
6. Халафян А.А. Statistica 6. Статистический анализ данных: Учебник – 3-е изд. – М.: Бином-Пресс, 2007. – 512 с.
Дата добавления: 2016-10-07; просмотров: 5100;











