Погрешности измерения ротамерами. Поверка ротамеров.
Среднюю квадратическую относительную погрешность измерения расхода при помощи ротаметра можно вычислить из соотношения (17.2.33)
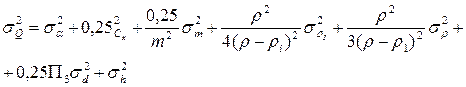 , (17.2.33)
, (17.2.33)
где 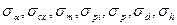 - соответственно средние квадратические отклонения величин
- соответственно средние квадратические отклонения величин 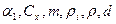 и h от их номинального значения.
и h от их номинального значения.
Пользование соотношением (17.2.33) затруднено, так как входящие в него величины определить бывает трудно, а подчас и невозможно, тем более что ротаметры обязательно подвергают градуировке и она по сути дает значение погрешности.
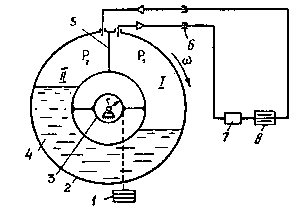
1 — груз; 2 — кольцевой мерник; 3 — блок; 4 — жидкость гидрозатвора; 5 — перегородка; 6 — уплотнения; 7 — градуируемый ротаметр; 8 — регулятор; I и II — полости.
Рисунок 17.2.13 - Газовая расходомерная установка с вращающимся кольцевым мерником
Но по соотношению (17.2.33) можно определить влияние отклонения параметров измеряемой среды на погрешность. Кроме основной погрешности при измерении ротаметрами могут возникнуть дополнительные погрешности, главной из которых является погрешность от отклонения оси ротаметра от вертикали, которую вычисляют по формуле (17.2.34)
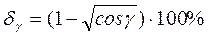 , (17.2.34)
, (17.2.34)
Поверку ротаметров проводят в соответствии с ГОСТ 8.122 – 99 «ГСИ. Ротаметры. Методы и средства поверки». Поверку жидкостных ротаметров проводят либо на специальных установках, либо на универсальных расходомерных поверочных стендах и установках. Поверку газовых ротаметров проводят на установках с образцовыми газовыми меринками. Схема одной из таких установок приведена на рисунке 17.2.13. Надо знать, что расходомерные установки для поверки и градуировки ротаметров должны быть аттестованы органами государственной метрологической службы или ведомственными метрологическими службами.
17.2.3 Пикнометры /31/
Устройство пикнометров
Пикнометрический метод определения плотности жидкости основан на взвешивании жидкости, занимающей в пикнометре известный объем, найденный весовым способом.
В сравнении с гидростатическим взвешиванием пикнометрический метод определения плотности обладает рядом преимуществ. Основные достоинства данного метода сводятся к следующему:
1) высокая точность измерений (до 1·10-5 г/см3), обусловленная тем, что взвешивают на высокоточных весах общего назначения без каких-либо дополнительных устройств, неизбежно уменьшающих чувствительность весов;
2) малая площадь свободной поверхности жидкости в пикнометре, что практически исключает испарение жидкости и поглощение влаги из воздуха;
3) пригодность для работы как с летучими, так и с весьма вязкими жидкостями;
4) возможность использования малого количества жидкости (1—100 см3);
5) раздельное проведение операций термостатирования жидкости в пикнометре и последующего взвешивания.
Поэтому при точных измерениях (например, при исследовательских работах), когда вполне оправданы некоторая трудоемкость и необходимость соблюдения ряда предосторожностей, пикнометрическому методу отдают предпочтение.
Существует много разновидностей пикнометров, и их применение определяется родом испытуемого вещества, его количеством, а также требуемой точностью измерений. Чем больше вместимость пикнометра, тем' меньше погрешность взвешивания; однако одновременно увеличивается ошибка, связанная с неравномерностью температуры во всей массе жидкости. Наилучшие результаты получают с пикнометрами вместимостью 25—100 см3.
Наиболее распространены стеклянные колбообразные пикнометры шаровидной и цилиндрической формы, которые закрываются либо глухой притертой пробкой (эти пикнометры имеют круговую метку на горле – рисунок 17.2.14 а - в), либо притертой пробкой с капиллярным отверстием (рисунок 17.2.14 б). Основные размеры шаровидных пикнометров по ГОСТ 7465— 67.
Пикнометры с меткой, нанесенной на вставной горловине (рисунок 17.2.14 в), применяют для определения плотности твердых тел.
Метка на горле пикнометра соответствует его номинальной вместимости; до этой метки и заполняют пикнометр. Пикнометры с меткой, применяемые для жидкости (рисунок 17.2.14 а), могут иметь номинальную вместимость 1; 2; 3; 5; 10; 50 и 100 см3, для твердых тел (рисунок 17.2.14 в) -10, 25 и 50 см3.
По требованию заказчика на расстоянии 1 мм выше и ниже основной метки наносят по одной дополнительной круговой метке, что упрощает пользование пикнометром.
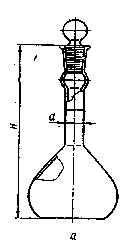
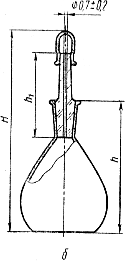
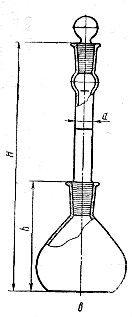
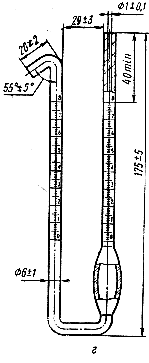
а, б; в — колбообразные шаровидные; г- - У-образный
Рисунок 17.2.14 - Стеклянные пикнометры.
Верхняя часть горла (под пробкой) пикнометра с меткой выполняется расширенной. В образующуюся расширенную полость входит часть жидкости в том случае, когда объем её увеличивается в результате повышения температуры после заполнения пикнометра до метки.
Пикнометр с капиллярным отверстием в пробке обеспечивает более точные результаты измерений. Диаметр отверстия (0,7 ± 0,2) мм. Вместимость такого пикнометра определяется верхним краем капиллярного отверстия.
Номинальная вместимость капиллярных пикнометров составляет 1; 2; 3; 5; 10; 25; 50 и 100 см3.
При измерении плотности сильно летучих жидкостей применяют II-образный капиллярный пикнометр, изображенный на рисунок 17.2.14 г. Согласно ГОСТ 7465—67 пикнометр представляет собой трубку с капиллярным отверстием диаметром от 0,9 до 1,0 мм. В правом колене имеется расширение. Конец левого колена отогнут. На обоих коленах нанесена равномерная шкала с 80 делениям (каждое деление - -1 мм). Номинальная вместимость 11-образного пикнометра, определяемая по нижней его части между нулевыми отметкам составляет 0,5; 1 и 3 см3.
Весьма удобен в работе пикнометр (рисунок 17.2.15) с боковой капиллярной трубкой 3. Пробкой служит тело термометра 1, пришлифованного к горлу колбы 4, Термометр позволяет вести непрерывные наблюдения за температурой жидкости. Отверстие капилляра закрывается колпачком 2, притертым к конусному концу трубки.
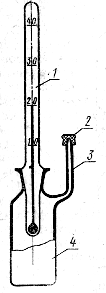
Рисунок 17.2.15 - Пикнометр с термометром.
Работа с пикнометром значительно упрощается, если на его горловине нанесена шкала, которая позволяет быстрее и точнее определять объем жидкости в пикнометре.
Для весьма малых количеств жидкости (порядка 1 см3) хорошие результаты получают с помощью пипеткообразного пикнометра (пикнометра Оствальда - Шпренгеля). Он представляет собой U-образную трубку с оттянутыми и отогнутыми под прямым углом концами. Оба конца трубки закрыты притертыми колпачками. Пикнометр заполняют жидкостью до края отверстия на одном конце и до метки на другом конце.
Для измерения плотности газов применяют шаровидные пикнометры вместимостью 100 и 200 см3 (ГОСТ 11723—66).
Определение плотности жидкости
Для определения плотности жидкости выполняют три взвешивания:
1) пустого пикнометра;
2) пикнометра, заполненного дистиллированной водой до заданного уровня;
3) пикнометра, заполненного испытуемой жидкостью до того же уровня. Первые два взвешивания позволяют определить вместимость пикнометра, а первое и третье — массу испытуемой жидкости в объеме пикнометра. По полученным данным подсчитывают плотность жидкости.
Выведем общую формулу для определения плотности жидкости при помощи пикнометра, когда вода и жидкость имеют разную температуру. Примем следующие обозначения:
- m1 - масса гирь, уравновешивающих пустой пикнометр в воздухе плотностью D1;
- m2 - масса гирь, уравновешивающих пикнометр с дистиллированной водой в воздухе плотностью D2 при температуре t2;
- m3 - масса гирь, уравновешивающих пикнометр с испытуемой жидкостью в воздухе плотностью D3 при температуре t3;
- V - объем стекла пикнометра;
- V2 - вместимость пикнометра до заданного уровня при температуре t2;
- V3 - то же, при температуре t3;
- 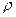 — плотность дистиллированной воды при температуре t2;
— плотность дистиллированной воды при температуре t2;
- 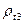 плотность испытуемой жидкости при температуре t3;
плотность испытуемой жидкости при температуре t3;
- Dm - плотность материала, из которого изготовлены гири;
- Dc - плотность стекла;
- 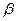 - коэффициент объемного расширения стекла.
- коэффициент объемного расширения стекла.
Условия равновесия весов при трех указанных выше последовательных взвешиваниях пикнометра можно записать в виде системы трех уравнений (17.2.35)
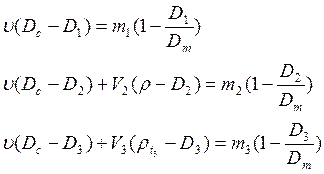 , (17.2.35)
, (17.2.35)
Определив из первого уравнения (17.2.35) значение v и подставив его во второе и третье уравнения, получим систему уравнений (17.36)
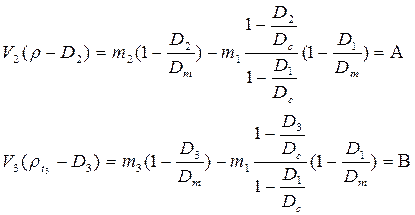 , (17.2.36)
, (17.2.36)
Величины V3 и V2 связаны между собой зависимостью (17.2.37)
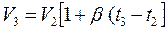 , (17.2.37)
, (17.2.37)
Разделив почленно уравнение два на уравнение 1 из системы уравнений (17.2.36) и учтя выражение (17.2.37), получим уравнение (17.2.38)

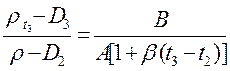 , (17.2.38)
, (17.2.38)
откуда для искомой плотности жидкости найдем окончательно
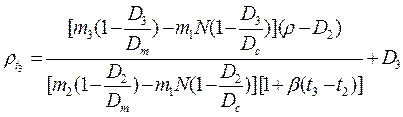 , (17.2.39)
, (17.2.39)
где 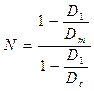
Выражение (17.2.39) учитывает все величины, влияющие на результат измерения плотности, и поэтому обеспечивает наивысшую точность измерения.
В ряде случаев при введении определенных условий формула (17.2.34) может быть значительно упрощена. Если плотность воздуха на протяжении периода, в течение которого выполняют взвешивания, остается постоянной, т. е. D1 =D2 =D3 = D, то формула (17.2.39) принимает вид (17.2.40)
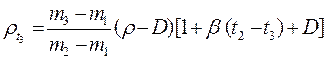 , (17.2.40)
, (17.2.40)
Обычно при работе с пикнометром выдерживают одинаковую температуру воды и жидкости, что дополнительно упрощает приведенную выше формулу. Действительно, при t1 =t2 =t
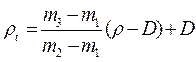 , (17.2.41)
, (17.2.41)
Определение плотности твердого тела
При измерении плотности твердого тела пикнометрическим методом также выполняют три взвешивания:
1)масса испытуемого тела в воздухе;
2)масса пикнометра, наполненного дистиллированной водой или какой-либо другой вспомогательной жидкостью известной плотности;
3)масса пикнометра, наполненного той же жидкостью с погруженным в нее испытуемым телом, причем в обоих случаях жидкость наливают до одного и того же уровня.
Уравнения равновесия при указанных взвешиваниях запишутся в виде (17.2.42)
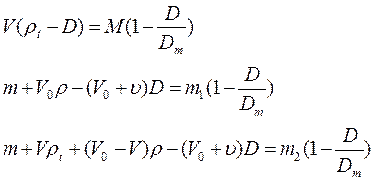 , (17.2.42)
, (17.2.42)
где V — объем стекла пикнометра;
V0 - вместимость пикнометра до заданного уровня;
V — объем испытуемого тела;
m - масса пустого пикнометра;
M — масса гирь, уравновешивающих тело в воздухе;
m1 - масса гирь, уравновешивающих пикнометр со вспомогательной жидкостью;
m2 - масса гирь, уравновешивающих пикнометр с жидкостью и погруженным в нее телом;
т0 - масса гирь, уравновешивающих пустой пикнометр;
р - плотность вспомогательной жидкости;
р1 - плотность испытуемого тела;
D — средняя плотность воздуха во время взвешиваний;
Dm - плотность материала, из которого изготовлены гири.
Указанные выше величины соответствуют температуре t , для которой определяют плотность рt тела. Уравнение равновесия, характеризующее взвешивание пустого пикнометра можно представить в виде (17.2.43)
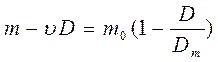 , (17.2.43)
, (17.2.43)
После вычитания уравнения (17.2.43) последовательно из второго и третьего уравнений (17.2.42) получим (17.2.44)
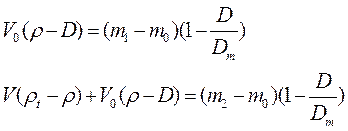 , (17.2.44)
, (17.2.44)
откуда почленным вычитанием найдем
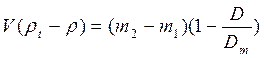 , (17.2.45)
, (17.2.45)
Подставив величину V из первого уравнения (17.2.42) в уравнение (17.2.45), после преобразований получим искомую формулу для определения плотности твердого тела (17.2.46)
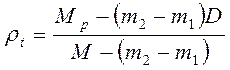 , (17.2.46)
, (17.2.46)
Дата добавления: 2016-10-07; просмотров: 2225;











