Самообучающиеся интеллектуальные системы

Среди экспертных медицинских систем особое место занимают так называемые самообучающиеся интеллектуальные системы (СИС). Они основаны на методах автоматической классификации ситуаций из реальной практики или на методах обучения на примерах. Наиболее яркий пример СИС -- искусственные нейронные сети.

Искусственные нейронные сети (ИНС; artificial neural networks) представляют собой нелинейную систему, позволяющую классифицировать данные гораздо лучше, чем обычно используемые линейные методы. В приложении к медицинской диагностике ИНС дают возможность значительно повысить специфичность метода, не снижая его чувствительность.

ИНС -- это структура для обработки когнитивной информации, основанная на моделировании функций мозга. Основу каждой ИНС составляют относительно простые, в большинстве случаев однотипные элементы (ячейки), имитирующие работу нейронов мозга. Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Искусственный нейрон обладает группой синапсов -- однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон -- выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов.

Для ИНС характерен принцип параллельной обработки сигналов, что достигается путем объединения большого числа нейронов в так называемые слои и соединения нейронов различных слоев. Теоретически количество слоев и количество нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера. В общем случае, чем сложнее ИНС, тем масштабнее задачи, подвластные ей. Прочность синаптических связей модифицируется в процессе извлечения знаний из обучающего набора данных (режим обучения), а затем используется при получении результата на новых данных (режим исполнения).

Наиболее важным отличием ИНС от остальных методов прогнозирования является возможность конструирования экспертных систем самим врачом-специалистом, который может передать нейронной сети свой индивидуальный опыт и опыт своих коллег или обучать сеть на реальных данных, полученных путем наблюдений. Нейронные сети способны принимать решения, основываясь на выявляемых ими скрытых закономерностях в многомерных данных.

Положительное отличительное свойство ИНС состоит в том, что они не программируются, т.е. не используют никаких правил вывода для постановки диагноза, а обучаются делать это на примерах. В ряде случаев ИНС могут демонстрировать удивительные свойства, присущие мозгу человека, в том числе отыскивать закономерности в запутанных данных. Нейронные сети нашли применение во многих областях техники, где они используются для решения многочисленных прикладных задач: в космонавтике, автомобилестроении, банковском и военном деле, страховании, робототехнике, при передаче данных и др.

Другое, не менее важное, свойство нейронной сети состоит в способности к обучению и обобщению полученных знаний. Сеть обладает чертами так называемого искусственного интеллекта. Натренированная на ограниченном множестве обучающих выборок, она обобщает накопленную информацию и вырабатывает ожидаемую реакцию применительно к данным, не обрабатывавшимся в процессе обучения.

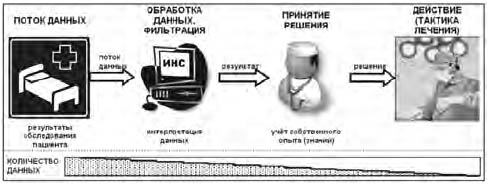
Рис. 1. Схема применения обученной искусственной нейронной сети в медицине

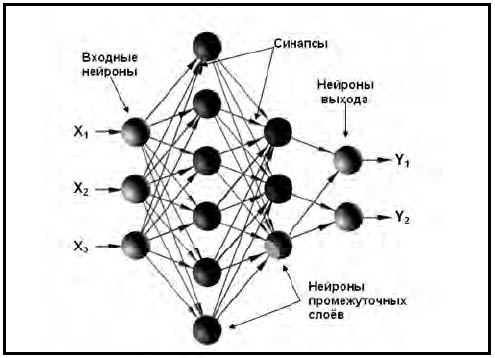
Схематично процесс применения обученной ИНС в медицине показан рис. 2

Несмотря на значительное количество уже известных практических приложений искусственных нейронных сетей, возможности их дальнейшего использования для обработки сигналов окончательно не исчерпаны,

Среди указанной группы методов классификации и распознавания наиболее интересным и гибким представляется метод опорных векторов (МОВ).

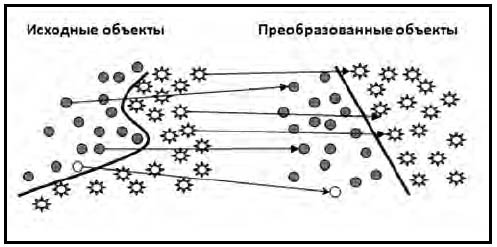
Метод опорных векторов (МОВ) - это метод первоначальной классификации, который решает данную задачу путем построения гиперплоскостей в многомерном пространстве, разделяющих группы наблюдений, принадлежащих к разным классам. На рис. 3 проиллюстрирована основная идея МОВ. В левой части схемы представлены исходные объекты, которые далее преобразуются (перемещаются, сдвигаются) в пространстве признаков при помощи специального класса математических функций, называемых ядрами. Этот процесс перемещения называют еще преобразованием, или перегруппировкой объектов. Новый набор преобразованных объектов (в правой части схемы) уже линейно разделим. Таким образом, вместо построения сложной кривой (как показано в левой части схемы) требуется лишь провести оптимальную прямую, которая разделит объекты разных типов. Затем метод отыскивает объекты, находящиеся на границах между двумя классами, которые называются опорными векторами, и использует их для принятия решений о принадлежности к тому или иному классу новых объектов, предъявляемых для распознавания.

Рис. 3. Основная идея метода опорных векторов

Таким образом, на основании анализа публикаций о применении экспертных систем в медицине можно сделать следующие выводы:

1. Медицинская нейроинформатика как наука находится пока на стадии накопления фактического материала.

2. Нейронные сети обладают чертами, так называемого искусственного интеллекта.

3. Современные технические возможности позволяют выйти на качественно новый уровень представления течения заболевания, а именно на основе экспертных автоматизированных технологий смоделировать типовое развитие патологического процесса. Экспертные компьютерные медицинские системы позволяют врачу не только проверить собственные диагностические предположения, но и обратиться к компьютеру за консультацией в трудных диагностических случаях.

ПЕРСПЕКТИВЫ РАЗВИТИЯ

Функционирование многих ИС носит целенаправленный характер . Типичным актом такого функционирования является решение задачи планирования пути достижения нужной цели из некоторой фиксированной начальной ситуации. Результатом решения задачи должен быть план действий - частично-упорядоченная совокупность действий. Такой план напоминает сценарий, в котором в качестве отношения между вершинами выступают отношения 'типа: "цель-подцель" "цель-действие", "действие-результат" и т. п.. Любой путь в этом сценарии, ведущий от вершины, соответствующей текущей ситуации, в любую из целевых вершин, определяет план действий.

Поиск плана действий возникает в ИС лишь тогда, когда она сталкивается с нестандартной ситуацией, для которой нет заранее известного набора действий, приводящих к нужной цели. Все задачи построения плана действий можно разбить на два типа, которым соответствуют различные модели: планирование в пространстве состояний (SS-проблема) и планирование в пространства задач (PR-проблема).

(SS-проблема)

В первом случае считается заданным некоторое пространство ситуаций. Описание ситуаций включает состояние внешнего мира и состояние ИС, характеризуемые рядом параметров. Ситуации образуют некоторые обобщенные состояния, а действия ИС или изменения во внешней среде приводят к изменению актуализированных в данный момент состояний. Среди обобщенных состояний выделены начальные состояния (обычно одно) и конечные (целевые) состояния. SS-проблема состоит в поиске пути, ведущего из начального состояния в одно из конечных.

Если, например, ИС предназначена для игры в шахматы, то обобщенными состояниями будут позиции, складывающиеся на шахматной доске. В качестве начального состояния может рассматриваться позиция, которая зафиксирована в данный момент игры, а в качестве целевых позиций - множество ничейных позиций. Отметим, что в случае шахмат прямое перечисление целевых позиций невозможно. Матовые и ничейные позиции описаны на языке, отличном от языка описания состояний, характеризуемых расположением фигур на полях доски. Именно это затрудняет поиск плана действий в шахматной игре.

PR-проблемы

При планировании в пространстве задач ситуация несколько иная. Пространство образуется в результате введения на множестве задач отношения типа: "часть - целое", "задача - подзадача", "общий случай - частный случай" и т. п. Другими словами, пространство задач отражает декомпозицию задач на подзадачи (цели на подцели). PR-проблема состоит в поиске декомпозиции исходной задачи на подзадачи, приводящей к задачам, решение которых системе известно. Например, ИС известно, как вычисляются значения sin x и cos x для любого значения аргумента и как производится операция деления. Если ИС необходимо вычислить tg x, то решением PR-проблемы будет представление этой задачи в виде декомпозиции tgx=a =sinx/cosx (кроме л:=л/2+k л).

Дадим классификацию методов, используемых при решении SS- и PR-проблем.

1. Планирование по состояниям. Представление задач в пространстве состояний предполагает задание ряда описаний: состояний, множества операторов и их воздействий на переходы между состояниями, целевых состояний. Описания состояний могут представлять собой строки символов, векторы, двухмерные массивы, деревья, списки и т. п. Операторы переводят одно состояние в другое. Иногда они представляются в виде продукций А=>В, означающих, что состояние А преобразуется в состояние В.

Пространство состояний можно представить как граф, вершины которого помечены состояниями, а дуги-операторами. Если некоторая дуга направлена от вершины n_i, к вершине n,, то п, называется дочерней, а n_j;-родительской вершинами