Подстановочно перестановочные сети (SPN-ы)

Следуя идеям Шеннона о путанице и распространении (confusion and diffusion), многие шифры построены с помощью применения слоистой подстановочно перестановочной (SP) структуры. Каждый слой имеет специальное назначение:

Подстановочный слой применяет нелинейную подстановку (замену) к шифруемому блоку. Нелинейная функция часто реализуются с помощью таблицы подстановки, которую обычно называют S-блоком. Этот шаг делается для того, что зависимость между открытым текстом, ключом и зашифрованный текст носила нелинейный характер.

Перестановочный слой смешивает разные части блока, часто с использованием линейной функции. Использованием более общих линейных или аффинных функций, чем простая перестановка мощность диффузионного преобразования может быть увеличена. Этот шаг гарантирует, что изменения в открытых текстов и ключей, разбросаны по всему блоку.

Ключевой смешивающий слой применяется ключ или подключ к блоку. Этот шаг смешивает ключ с блоком делая отношение (связь) между плайнтекстом и ключом зашифрования зависимой. Смешивание ключа с блоком часто выполняется с помощью XOR или модульного сложения.

Как уже отмечалось, нет никаких причин не использовать более общую линейную функцию чем транспозиции в перестановочном слое. Такой шифр можно назвать Подстановочной Линейной Сетью (Substitution Linear Network) (SLN), но мы будем придерживаться чаще используемого термина подстановочно перестановочной схемы.

Пример двух циклов итеративной подстановочно перестановочной схемы показан на Рис.1.

Рис. 1. Два цикла подстановочно перестановочной схемы

Фестелевы шифры

Фестелевы шифры являются классом подстановочно перестановочных сетей с особой (специальной) структурой. Изобретенная Хорстом Feistel-ем [20], общая структура (как показано на рис. 2.2) была использована в ряде блочных шифров, таких как DES [46] и Blowfish [53].

Входной блок делится на две половины, L₀ и R₀, которые затем обновляются, используя некоторую произвольную функцию f и рекурсию

R_i = L_{i -1} Å f(k_{i -1}, R _{i -1});

L_i = R_{i -1},

где k_i-1 является используемым подключом. Эта конструкция всегда обратима, даже если f нет. Если своп остается в последнем цикле, дешифрование равно шифрованию с подключом k_i в обратном порядке. Это преимущество, так как реализация того же куска кода шифрования и дешифрования может быть сделана только с изменением индексации подключей.

Цикловые Функции

Как упоминалось ранее, блочных шифров часто строятся путем итерации относительно простой функций, называемых цикловыми функциями, несколько раз. Общим для создания цикловой функции является то, что она состоит из двух компонент, нелинейной функции и линейного преобразования. В этом разделе рассматриваются некоторые идеи, использованные в конструкции цикловых функций.

Нелинейные функции

Нелинейная функция блочного шифра является основным источником криптографической стойкости, и многие исследования были сделаны в этой области. Общим является использование небольшой функции параллельно на входе цикловой функции. Блок может быть, например, разбит на байты с последующим применением некоторой функции для каждого байта в индивидуальном порядке. Эти небольшие функции часто строятся на основе таблиц, и называются S-блоками. Размер S-блоков записывается как m´n, где n является числом входных битов, а m числом выходных битов. Общепринятые размеры S-блоков 8×8, 6×4 и 8×32.

Можно выделить три подхода к дизайну нелинейных функций:

Случайно выбранные S-блоки были использованы в ряде шифров. Некоторые, такие как Blowfish [53] используют ключезависимые случайно выбранные S-блоки.

Отобранные и протестированные S-блоки были использованы в нескольких шифрах. Одним из примеров является Khazad [3], в котором используется фиксированный, случайно сгенерированный S-блок, проверенный на выполнение определенных свойств при проектировании шифра.

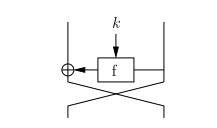
Рис.2. Фестелева структура

Математически порожденные (сгенерированные) S-блоки строятся с использованием некоторых математических функций. Одним из примеров такого подхода представлен в работе [51]. Шифры, использующие этот тип S-блоков включают Rijndael [19] и Safer++ [38].

Каждый из этих подходов поставляется с преимуществами и недостатками. Случайно выбранным S-блокам обычно не хватает структуры, которая могла бы помочь криптоаналитику, но при ключезависимо порожденных S-блоках могут быть ключи, которые в некотором отношении генерируют слабые S-блоки. Модульные умножения, применённые в IDEA [32] [33], могут рассматриваться как ключезависимые случайно выбранные S-блоки и IDEA действительно имеет слабые ключи, как показано в [17], [23] и [11].

Математически порожденный S-боксы могут быть построены, чтобы иметь ряд желательных свойств по отношению к атакам, таких как дифференциальный и линейный криптоанализ. Одним из примеров является S-блоки, использованные в Rijndael-е, который основан на инверсии в конечных поле. Тем не менее, необходимо соблюдать осторожность, чтобы избежать атак, таких как интерполяционная и другие атаки [24], в которых используются математические структуры шифра. Например, в шире Safer++ математическая структура S-блоков может быть использована для улучшения атаки.