Некоторые из известных феноменов, открытых Ж. Пиаже у детей в возрасте до 7-8 лет.

Затем следует фаза «интеллектуального реализ­ма», когда топологические отношения уже соблюдаются, но ребенок еще не координирует разных точек зрения на предмет (проективные отношения) и рисует объект не так, как он выглядел бы с какой-то определенной точки зрения, а так, как этот объект ему известен. Для этой фазы характерен рисунок, на котором разные части предмета представлены в раз­ных ракурсах, «рентгеновские рисунки» и т. д. Нако­нец, с овладением проективными и эвклидовыми отношениями ребенок вступает в фазу «зрительно­го реализма».

В экспериментальных исследованиях Пиаже рас­смотрел становление проективных отношений (рис. 13-2, 13-3, 13-4, 13-5). Он изучал предсказа­ния детей по поводу формы теней, которые будут отбрасывать предметы при различном их повороте по отношению к источнику света; по поводу того, как будет выглядеть макет, находящийся на столе экспериментатора, при взгляде с другой стороны.

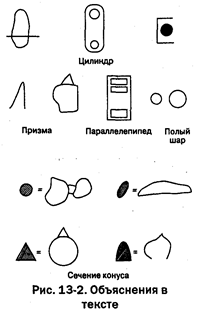
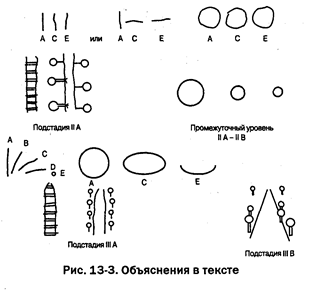
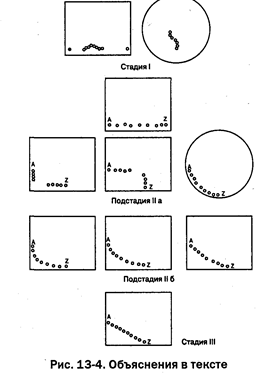
На рис. 13-2 показано, каким образом дети представляют себе сечения некоторых трехмерных фигур. На рис. 13-3 представлены изображения детьми уходящих вдаль рельсов, дороги с тополями и того, как будут видны стрелка и диск при разных углах их поворота. Рис. 13-4 представляет попытки детей разного возраста построить на круглом и прямоугольном столе из игрушечных столбиков прямую линию («линию электропередачи») между столбиками А и В, установленными экспериментатором.

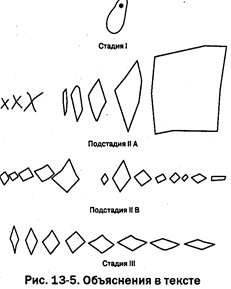
Пиаже показал также постепенное становление эвклидовых отношений в экспери­ментах по подобию фигур и изображению горизонтали (линии воды в наклонных сосудах). На рис. 13-5 представлено изображе­ние детьми аффинных трансформаций (из­менение углов, но не длин сторон) ромба.

Идея работ по времени, скорости и дви­жению возникла у Пиаже, по его собствен­ным словам, в беседах с А. Эйнштейном. Здесь тоже получено немало интересных фактов. Показано, что понятие времени у детей до 7 лет сливается с понятием рассто­яния. Ребенок отказывается признать, что два поезда двигались одинаковое время, если они прошли разное расстояние.

Он готов считать, что человек А, родив­шийся раньше человека В, может быть тем не менее моложе, чем В. В эксперименте с водой, льющейся из резервуара в два раз­ных по форме сосуда, было показано, что время наполнения этих сосудов оказыва­ется зависимым в сознании ребенка от фор­мы этих сосудов. Пиаже говорит, что для ребенка существует как бы множество ло­кальных, связанных с различными объек­тами времен, которые лишь на стадии кон­кретных операций объединяются в единое ньютоновское время.

С 7-8 и до 11-12 лет формирование понятий, о которых говорилось выше, в основ­ном завершается, и описанные феномены у детей исчезают. Однако развитие интеллекта на этом не останавливается. У подростков, согласно Пиаже, должен еще сформироваться так называемый формальный интеллект. Формальный интеллект представляет со­бой интеллект второго уровня, операции над операциями. Он включает способность к рефлексивному и гипотетико-дедуктивному мышлению, комбинаторике и т. д.

Пиаже, безусловно, удалось добиться впечатляющих результатов. К 1960-м гг. его теория стала доминирующей в области психологии развития интеллекта. Но оборот­ной стороной повсеместного признания стала усиливающаяся критика (Ушаков Д. В., 1995). В 1970-х и 1980-х гг. было обнаружено столько эмпирических проблем, что теория стадий и теория групп были отвергнуты большинством исследователей.

Наиболее существенной проблемой для теории Пиаже явился «декаляж», то есть неодновременность появления в онтогенезе функций, которые оцениваются теорией как структурно одинаковые. Если учесть, что одновременность онтогенетического развития различных функций является одним из основных положений теории стадий, то легко понять, насколько сильным разрушительным действием обладает декаляж. Собственно феномен декаляжа был открыт и назван самим Пиаже, который, однако, вначале отводил ему роль частного явления, исключения, подтверждающего правило. Со временем выяснилось, однако, что декаляж имеет весьма общий характер.

Исследователи с определенного момента нацелились на то, чтобы показать как можно более раннее появление у ребенка тех функций, которые, согласно Пиаже, должны возникать на стадии конкретных операций, те есть в 7-8 лет. Так, Т. Трабассо на материале сериации, П. Муну и Т. Бауер на сохранении, А. Старки в области понятия числа, Е. Маркман на включении множеств сумели таким образом видоизменить задачи Пиаже, что дети решали их в 5 лет вместо 7-8.

Рассмотрим для примера задачу Пиаже на включение. Е. Маркман предложил заменить название класса собирательным классом. Oн предъявлял детям семь цветков — пять мар­гариток и два тюльпана. На традиционный вопрос Пиаже —«Чего больше: цветков или маргариток?» — дети правильно отвечают не раньше, чем в 7 лет. Но на вопрос Маркмана — «чего больше: цветков в букете или маргариток?» — правильный ответ дети дают значительно раньше. Г. Политцер показал аналогичный результат при вопросе: «Чего больше: маргариток, тюльпанов или цветов?» (Политцер Г., Жорж К., 1996).

Дж. Флейвелл подытожил: маленькие дети способны на большее, чем считал Пи­аже, а подростки и взрослые — на меньшее. Важно подчеркнуть, что было показано раннее возникновение оперирования с отношениями, но в строго определенных об­легченных экспериментальных условиях.

В настоящее время теория Пиаже находится в довольно своеобразном положе­нии: с одной стороны, практически никто из современных исследователей развития интеллекта не может обойтись без ссылок на факты и их объяснения, данные Пиаже; с другой — никто с Пиаже не согласен. Кроме того, накоплено много новых фактов. Открыты новые сферы, где наблюдаются феномены, сходные с описанными Пиаже.

Одной из наиболее интересных сфер оказалось развитие детских представлений о психике (child's theory of mind). В известной работе Виммера и Пернера детям расска­зывали про некий персонаж (Макси), который видит, как шоколадку прячут в опре­деленном месте (на кухне). В то время, как Макси уходит, шоколадку из кухни пере­носят в другое место — в столовую. Теперь Макси возвращается и хочет шоколадку. Детям задают вопрос: где Макси будет искать — на кухне или в столовой? Получен­ные результаты (дети до 4 лет предполагают, что Макси будет искать в столовой) были интерпретированы в том смысле, что маленькие дети не отличают мысли о пред­метах (мысль о шоколадке у Макси) от самих предметов (шоколадка).

Некоторые другие факты трудно соотнести с теорией Пиаже. Одни из них, как говорилось выше, свидетельствуют о наличии декаляжей. Другие требуют большего количества подстадий, чем это вытекает из теории Пиаже. К сожалению, в настоящее время не создано синтетической теории, которая могла бы адекватно объяснить все полученные факты. Некоторые теоретики отошли от идеи стадий (Ж. Верньо) и рас­сматривают умственное развитие как состоящее из множества локальных шагов, связанных с овладением отдельными понятиями.

Неоструктуралисты же сохранили представление о стадиальности развития. Од­нако они интерпретируют эти стадии по-своему. С их точки зрения, особенности дет­ского интеллекта можно объяснить способами переработки информации. Наиболее часто при этом обращаются к идее детерминации стадий интеллектуального разви­тия объемом кратковременной памяти.

X. Паскуаль-Леоне, Р. Кейс, К. Фишер и другие считают, что решение сложных задач предполагает возможность одновременно удерживать в сознании значитель­ное число элементов. Способность одновременного удерживания нескольких элемен­тов развивается постепенно (по X. Паскуаль-Леоне, на одну единицу за два года с возраста от 3 до 15 лет), чем и определяется появление стадий в интеллектуальном развитии.

Процесс мышления

Как говорилось выше, мышление предполагает создание модели проблемной си­туации и вывод внутри этой модели. Модель создается не на пустом месте, а из «стро­ительных элементов», различных структур репрезентации знаний, находящихся в долговременной памяти. Из этих элементов в поле внимания создается модель, отно­сящаяся только к данной задаче. Мышление, таким образом, — процесс комплекс­ный, в нем задействованы многочисленные психические структуры и процессы, рас­сматриваемые в других главах учебника.

Первая теория, описывающая процесс мышления, была предложена еще в XIX в. в рамках ассоциативной психологии. Ассоцианисты полагали, что душевная жизнь определяется борьбой между отдельными элементами (идеями) за место в сознании. Объем сознания ограничен, в нем одновременно может находиться небольшое число элементов. Элементы притягивают к себе некоторые другие, т. е. пытаются ввести их в поле сознания, если сами там находятся. Это притяжение между элементами (ассо­циация) происходит либо в результате совместного наличия в прошлом опыте, либо по сходству. Например, если наблюдение молнии в моем прошлом опыте сопровож­далось тем, что я слышал удар грома, то, вероятно, идея молнии в моем сознании вы­зовет идею грома. Но также возможно, что эта идея произведет ассоциацию по сход­ству, например, я подумаю о змее.

Ассоцианисты описывают мыслительный процесс примерно следующим образом. В поле сознания при получении субъектом задачи попадает одновременно условие задачи и цель, которой требуется достигнуть. Условие задачи и цель будут способ­ствовать тому, что в поле сознания попадет такой средний элемент, который связан и с условием задачи, и с целью. Например, если нас спрашивают, смертен ли Сократ, то в нашем сознании появляется идея человека, которым является Сократ и который смертен. По мнению ассоцианистов, мышление начинается с создания представле­ния о проблемной ситуации. Правда, проблемная ситуация понимается ими не как структура, а только как сумма элементов: неважно, в каких отношениях находятся условие задачи и цель, важно лишь, что они присутствуют в сознании.

В современной когнитивной психологии обычно выделяются два этапа в процессе мышления: этап создания модели проблемной ситуации и этап оперирования с этой моделью, понимаемый как поиск в проблемном пространстве. Хотя, как будет видно из дальнейшего, это разделение достаточно условно, мы будем излагать материал в соот­ветствии с этими этапами.

Модель проблемной ситуации возникает не на пустом месте: в ее создании уча­ствуют структуры и схемы знания, находящиеся в долговременной памяти. Здесь про­исходят те же процессы поиска и извлечения знаний, что и рассматриваемые иссле­дователями памяти. Разница, однако, заключается в том, что процесс мышления требует создания из известных элементов новой модели, тогда как память предпола­гает простое извлечение того, что было в нее заложено.

Что должна представлять собой создаваемая умственная модель? Рассмотрим две следующие задачи: «На ветке сидело шесть птиц, четыре улетели. Сколько осталось?» и «У Пети было шесть конфет, он съел четыре. Сколько осталось?». Хотя в двух слу­чаях речь идет о совершенно разных объектах, задачи имеют идентичную структуру и для своего решения предполагают одинаковую умственную модель, из которой ис­ключаются семантические подробности и сохраняется лишь «остов», включающий саму структуру, то есть элементы и их отношения. У объектов обрубаются их излиш­ние в контексте задачи семантические характеристики.

Как показывают факты, задачи, обладающие одинаковой структурой при разном содержании, неодинаково сложны для субъекта. Это означает, что структуры хра­нятся в долговременной памяти вместе с семантической информацией. Другими сло­вами, объекты, о которых мы думаем, уже подталкивают нас к тому, чтобы поставить их в контекст той или иной структуры.

Компьютерная модель ИСААК, разработанная в 1977 г. Дж. Новаком, создает на основании текста школьных задач из области физической статики систему уравне­ний, которую затем пытается решить, и рисует чертеж условий задачи. Лингвисти­ческий анализ, проводимый ИСААКом, стремится свести условия к одному из «ка­нонических рамочных объектов», содержащихся в памяти системы, таких, как твердое тело или массивная точка. Один и тот же физический объект может быть сведен к разным «каноническим рамочным объектам». Например, человек, переносящий доску, может интерпретироваться как точка опоры, а тот же человек, сидящий на доске, — как массивная точка. На следующем этапе ИСААК устанавливает взаимное располо­жение объектов, создает на этом основании систему уравнений и рисует чертеж из набора стандартных фигур, зафиксированных в его памяти.

ИСААК моделирует самый простой вариант понимания задачи, при котором уже зафиксирован исходный небольшой набор операциональных структур и существуют простые правила перевода ситуации в эти структуры. Сам же перевод задачи в ум­ственную модель может быть связан и с серьезными трудностями.

Г. Саймон, единственный в настоящее время лауреат Нобелевской премии среди психологов, предложил в 1960-х гг. новое представление процесса решения задач. Рас­смотрим это представление на примере шахмат, которые называют дрозофилой когнитивной психологии, поскольку, подобно дрозофиле, шах­маты являются удобной моделью изучения других, выходя­щих за рамки лаборатории явлений, но, как и дрозофила, сами по себе мало интересуют психологов.

В изображенной на рис. 13-6 позиции из шахматной партии черные могут выбрать один из 35 ходов, разрешен­ных правилами игры. В ответ на каждый из этих ходов у бе­лых есть примерно такое же количество продолжений и т. д. Представим теперь себе эту ситуацию в виде лабиринта. Тогда исходное положение мы можем интерпретиро­вать как комнату, из которой выходит 35 коридоров, каждый из которых ведет в дру­гую комнату, из которой в свою очередь выходит какое-то количество коридоров, ве­дущих в новые комнаты.

Этот лабиринт в решении задачи Саймон предложил называть пространством по­иска. Ту часть лабиринта, которую субъект уже обследовал к данному моменту реше­ния задачи, Саймон назвал проблемным пространством. С формальной точки зрения, для решения задачи субъект должен произвести такое обследование лабиринта, кото­рое позволит ему найти путь к цели, в случае шахмат — к выигрышу партии. Оптималь­ным для этого было бы осуществление исчерпывающего поиска, то есть обхода всех коридоров лабиринта. К сожалению, на практике это оказывается невозможным.

Вернемся к позиции, изображенной на рис. 13-6. Игравший в ней черными А. Але­хин сделал ход 33.... Фb5-d7+, который, по его собственным словам, был рассчитан на 21 ход (или 41 полуход, то есть ход каждой из сторон) вперед, после чего партия переходила в теоретически выигранный для черных пешечный эндшпиль. Конечно, подобная глубина расчета нетипична: по словам самого Алехина, это наиболее длин­ная комбинация, рассчитанная им во время практической партии.

Попробуем оценить, сколько вариантов шахматист должен бы был в этом случае рассчитать, если бы он действовал методом полного перебора. Если даже принять, что на каждом ходу был выбор в среднем только из 10 возможностей, то нужно было бы рассчитать 10⁴¹ вариантов. Это означает, что при скорости счета 1 ход в секунду Алехин, начав расчет в 1922 г., не только не закончил бы его к началу XXI в., но и провел бы в раздумьях без сна, еды и отдыха еще миллиарды лет. Ясно, что такие чудовищные цифры перебора вариантов не имеют никакого отношения к реальному человеческому мышлению, хотя методом полного перебора действует большинство современных шахматных компьютеров, в том числе и Deep Thought, победивший чем­пиона мира Г. Каспарова.

Для объяснения способности человека выбирать в ходе решения задачи наиболее осмысленные варианты было введено понятие «эвристика», то есть такой метод поиска, который со значительной вероятностью позволяет отбирать наиболее удачные спосо­бы решения задачи. Рассмотрим пример одной из таких эвристик, пожалуй, наиболее простой. Она называется «эвристикой самого крутого подъема». Представим себе че­ловека, прогуливающегося по неровной местности и поставившего себе цель забрать­ся на вершину самого высокого холма. Местность испещрена тропинками, которые постоянно ветвятся. Для того чтобы сократить число неудачных попыток, человек может воспользоваться правилом: выбирать всегда ту тропинку, которая круче всех поднимается вверх. Это и есть эвристика самого крутого подъема.

· Эвристика — метод поиска, который со значительной вероятно­стью позволяет отби­рать наиболее удачные способы решения, задачи.

Итак, эвристики позволяют сократить дерево пере­бора. Но являются ли они адекватным описанием чело­веческого мышления? Вряд ли на этот вопрос можно ответить положительно. Конечно, в ситуации прогул­ки по пересеченной местности рассмотренная эврис­тика действительно может применяться человеком. Но выбор тропинки, ведущей вверх, не идет ни в ка­кое сравнение по насыщенности мыслительной дея­тельности с теми же шахматами, а в отношении реше­ния собственно интеллектуальных задач применение эвристики кажется маловероятным.

Описанная эвристика, как, впрочем, и все другие, не гарантирует успеха: самый крутой подъем может вести на вершину не самого высокого, а второстепенного холма, все же эвристика увеличивает вероятность того, что рассматриваемый вариант ведет к успеху. Легко можно представить, как приложить такую эвристику к другим задачам. Например, в шахматах она может означать первоочередное рассмотрение ходов, приводящих к ма­териальному перевесу, занятию центра фигурами, ослаблению прикрытия вражеско­го короля и т. д. Используя несколько более изощренный вариант рассмотренной выше эвристики (так называемый «анализ целей и способов»), А. Ньюэлл и Г. Сай­мон создали программу «Общий решатель задач», которая оказалась способной, в частности, доказать 2/3 теорем одного известного математического трактата.

Вновь возьмем для примера шахматы. Фактически в процессе размышления над ходом происходит не столько выбор из вариантов, сколько включение в модель но­вых отношений между фигурами. Любая достаточно сложная шахматная позиция включает очень большое число отношений между фигурами. Создавая модель ситуа­ции, шахматист по необходимости отбирает только некоторые из них, наиболее су­щественные с его точки зрения. На основе этих отношений и строится «проблемное пространство». В процессе обдумывания выявляются новые отношения, те, которые раньше не воспринимались как существенные. Например, установление угрозы вил­ки с какого-либо поля делает существенным отношение фигуры, защищающей это поле. Только наличие представлений об отношениях фигур может объяснить такие употребляемые при анализе партии термины как угроза, защита, подготовка хода.

Психологически поиск в проблемном пространстве неотличим от предыдущего этапа — создания представления о задаче. Появление какого-либо хода среди рас­сматриваемых шахматистом при обдумывании есть результат установления отноше­ний фигур, которые и составляют представление о ситуации. Для объяснения того, что происходит при размышлении шахматиста над ходом, можно воспользоваться термином С. Л. Рубинштейна «анализ через синтез»: выявление новых отношений фигур (анализ) происходит в результате переосмысления позиции и постановки но­вых целей (синтез).

А. В. Брушлинский (1979, с. 154-159) пишет: «...Человек ищет и находит решение мыслительной задачи не по принципу выбора из альтернатив, а на основе строго опре­деленного, непрерывного, но не равномерно формирующегося прогнозирования иско­мого». И далее: «...Наши эксперименты показывают, что заранее данные, равновероят­ные и четко отделенные друг от друга альтернативы выбора могут стать таковыми не в начале, а лишь к концу предшествующего им живо­го процесса мышления. Вот почему, даже когда в ходе такого процесса субъект последовательно ана­лизирует несколько формируемых им способов ре­шения задачи, этот сам по себе существенный факт все же не означает дизъюнктивной ситуации выбо­ра из соответственно нескольких альтернатив. Что­бы выступить в качестве альтернатив, они должны сначала возникнуть и постепенно сформироваться. Полностью сформироваться они могут лишь в кон­це, в результате живого мыслительного процесса... мышление выступает как выбор из альтернатив не в психологическом, а в формально-логическом пла­не (когда акцент ставится на уже готовые продукты мыслительной деятельности безотносительно к живому психическому процес­су, в результате которого они формируются)».