В свою очередь, управляющее воздействие на входе ГУН

Е_УПР(р) = I_ЧФД(j_ОП - j_ГУН) Н_ФНЧ(р),

где I_ЧФД(j_ОП - j_ГУН) – функция, описывающая зависимость выходного (в данном случае токового) сигнала ЧФД от разности фаз на его входах, Н_ФНЧ(р) –передаточная функция петлевого фильтра, имеющая в данном случае размерность сопротивления.

Введем обозначение ошибки слежения по фазе j = j_ГУН - j_ОП; кроме того, учтем, что характеристика ЧФД на рабочем участке линейна (рис. 7.7.8, а также рис. 7.7.5); крутизна линейного участка характеристики ЧФД S_ЧФД = I_{ЧФД макс} / 2p, тогда

Е_УПР(р) = I_{ЧФД макс} Н_ФНЧ(р) j / 2p.

С учетом введенных обозначений, пользуясь заменой j_ГУН = j + j_ОП, запишем выражение для частоты ГУН w_ГУН иначе:

рj + W_у Н_ФНЧ(р) j = w_{ГУН СВ.} - рj_ОП,

где W_у = S_ГУН I_{ЧФД макс} – максимальное отклонение частоты ГУН под действием управляющего напряжения, т.е. полоса удержания системы ФАПЧ.

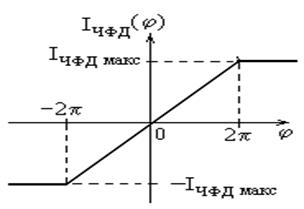
Рис.7.7.8.

Поскольку частота опорного генератора постоянна, в последнем уравнении можно сделать обратную замену рj_ОП = w_ОП, тогда его правая часть приобретает очевидный смысл начальной расстройки частоты ГУН относительно частоты опорного генератора, которую далее обозначим как Dw = w_{ГУН СВ.} - w_ОП:

рj + W_у Н_ФНЧ(р) j = Dw.

Полученное уравнение является основным дифференциальным уравнением системы ФАПЧ в операторной форме [20, 24-26]. Можно сделать вывод, что в общем случае начальная расстройка частоты ГУН относительно частоты опорного генератора Dw влияет на величину рассогласования фазы j, т.е. в общем случае система ФАПЧ не обладает астатизмом, но наличие интегратора в составе петлевого фильтра может решить эту проблему.

Петлевой фильтр схемы на рис. 7.7.6 состоит из интегратора – конденсатора С_инт и изодромного звена - цепочки R_из, С_из. Его передаточная функция

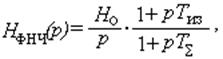
где Н₀ = 1/(С_из + С_инт), Т_из = R_изС_из, Т_S = Н₀R_изС_из С_инт.

Подставляя это выражение для передаточной функции петлевого фильтра в приведенное выше общее уравнение системы ФАПЧ и учитывая, что Dw не является функцией времени (т. е. рDw=0), получаем дифференциальное уравнение в операторной форме следующего вида:

Т_S р³j + р²j +W_у Н₀ Т_из рj +W_у Н₀j = 0.

Итак, наличие в выражении Н_ФНЧ(р) множителя 1/р, соответствующего операции интегрирования, привело к тому, что начальная расстройка частоты ГУН относительно частоты опорного генератора Dw уже не влияет на величину рассогласования фазы в установившемся синхронном режиме j, Иными словами, система ФАПЧ, построенная с использованием комбинации ЧФД с токовым выходом и ФНЧ с интегрирующим конденсатором, обладает свойством астатизма.

Что касается изодромного звена, то оно обеспечивает устойчивость петли ФАПЧ и в режиме синхронизма позволяет минимизировать временную задержку Dt между одноименными перепадами импульсов, поступающих на входы ЧФД. У современных ЧФД Dt измеряется наносекундами. Следовательно, сам ЧФД является источником рассогласования по фазе Dj = w_сравнDt. Например, для случая, когда частота сравнения 200 кГц (стандарт GSM) и Dt = 1 нс получаем Dj = 0.072°.

Еще раз подчеркнем, что для достижения астатизма необходимо идеальное качество (отсутствие утечек тока и эффекта памяти по напряжению) конденсаторов фильтра, бесконечное входное сопротивление управляющего входа ГУН (или идеальный буферный каскад) и т.д. В реальных схемах достигается так называемый квазиастатизм, т.е. небольшое рассогласование по фазе всегда будет иметь место.