Деформации при сдвиге

Рассмотрим деформацию квадратного элемента при сдвиге.

Рис.4.5. Деформация квадратного элемента при сдвиге.

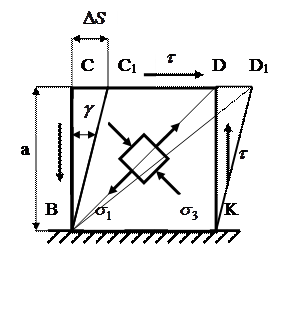Поскольку по граням элемента не действуют нормальные напряжения, то вдоль граней нет и удлинений. В то же время диагональ BD, совпадающая с направлением 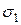, удлинится, а диагональ СК, совпадающая с направлением сжимающего напряжения 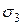, укоротиться. В результате квадрат BCDK трансформируется в ромб BC₁D₁K, без изменения длины граней. Таким образом, деформация сдвига характеризуется изменением первоначально прямых углов.

Малый угол 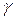, на который изменяется первоначально прямой угол элемента при сдвиге, называется
углом сдвига или относительным сдвигом.

Величину абсолютного смещения грани обозначают 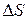и называют абсолютным сдвигом.

Из прямоугольного треугольника ВСС₁:

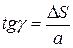(4.6)

Учитывая малость угла можно считать, что 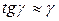, тогда окончательно запишем взаимосвязь между относительным и абсолютным сдвигом элемента

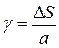(4.7)

При сдвиге можно экспериментально построить диаграмму сдвига, аналогичную диаграмме растяжения, на которой также в начале нагружения будет прямолинейный участок деформации по закону Гука.

Закон Гука при сдвиге:

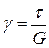или 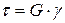, (4.8)

где G – модуль касательной упругости или модуль сдвига (модуль упругости второго рода), которая является константой для данного материала.

Закон Гука при сдвиге через абсолютные деформации:

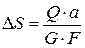, (4.9)

где а – расстояние между сдвигаемыми гранями; F – площадь грани.

Взаимосвязь между упругими постоянными:

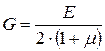. (4.10)