К ВОЗБУЖДЕНИЮ ОТ ПОСТОЯННЫХ МАГНИТОВ

Основным активным элементом магнитных цепей с постоянными магнитами является непосредственно сам постоянный магнит (ПМ). Постоянный магнит характеризуется частью петли гистерезиса, расположенной во втором квадранте декартовой системы координат с осями координат В и Н, где В - напряжённость магнитного поля в теле магнита, А/м; В - индукция магнитного поля в теле магнита, Тл.

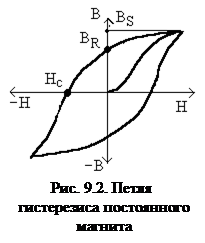Как видно из рис. 9.2, при напряжённости равнойнулю, индукция в теле магнита равна остаточной индукции B_R, а при индукции равной нулю напряжённость равна H_c – коэрцитивной силе.B_R и H_c – параметры постоянного магнита, приведенные в справочнике. Полное намагничивание постоянного магнита характеризуется индукцией полного намагничивания B_s.Намагничивание и размагничивание ПM производят в специальных намагничивавщих установках, простейший вид которых показан на рис. 9.3.

При пропускании тока по обмотке изменяется напряжённость и индукция в магнитной цепи. Связь между индукцией и напряжённостью имеет следующий вид

B=mH, (9.4)

где В – индукция в магнитопроводе,Тл; Н – напряжённость в магнитопроводе, А/м; m – магнитная проницаемость всей магнитной системы.

В случае, когда ток в обмотке равен нулю напряжённость также рав­на нулю, тем не менее в магнитопроводе имеется остаточный поток, обусловленный индукцией В_r.

Кроме основных параметров B_r и H_c постоянный магнит характеризуется удельной магнитной энергией W (рис. 9.5)

.

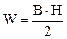Координаты точки кривой размагничивания при максимальной энергии постоянного магнита являются: В_d – индукция в теле магнита в точке кривой размагничивания с максимальной энергией, Тл; Н_d – напряженность в теле магнита в точке кривой размагничивания с максимальной энергией, А/м.

Если магнитная цепь замкнута и ненасыщена (m = ¥), тогда по выражению 9.4 Н = 0. Однако, на практике такие цепи встречаются редко, т.к. в действительности магнитная система имеет рабочий воздушный зазор (немагнитный). Рассмотрим случай, когда магнитная система имеет воздушный зазор, а сталь магнитопровода ненасыщена (m_ст = ¥). Тогда проводимость всей цепи будет определяться проводимостью воздушного зазора (рис. 9.6).

Рисунок 25.2 Намагничивающее устройство

По аналогии с электрической проводимостью сопротивление электрического проводника

,

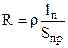где r – удельное сопротивление материала, Ом×мм²/м; l_п – длина проводника,м; S_пр – сечение проводника, м².

Проводимость электрического провода будет величиной обратной его сопротивлению, Сименс

.

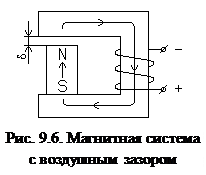
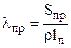Следовательно, для магнитной цепи проводимость будет равна, Гн

,

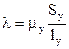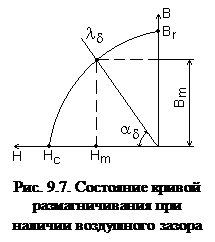где S_y – сечение участка магнитной цепи, м²; l_y – длина участка магнитной цепи, м; m_у – магнитная проницаемость участка магнитной цепи, Гн/м.

В рассматриваемом случае, при наличии воздушного зазора d и m_ст = ¥ проводимость всей цепи будет определяться проводимостью воздушного зазора

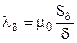
где m₀ – магнитная постоянная (m₀ = 4p×10^-7 Гн/м); S_d – площадь воздушного зазора, м²; d – длина воздушного зазора, м.

Здесь проводимость всего магнитопровода не равна бесконечности, следовательно, в теле магнита по 9.4 имеем напряженность

,

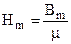где m ¹ ¥.

Положение на кривой намагничивания показано на рис. 9.7. Здесь В_m– индукция в нейтральном сечении магнита, Гн; Н_m – напряженность в нейтральном сечении магнита, А/м; l_d – проводимость воздушного зазора, Гн; a_d– угол наклона луча магнитной проводимости

.

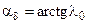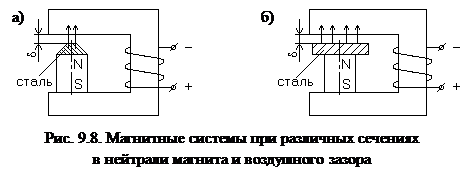
В действительности сечение магнита не всегда равно сечению воздушного зазора, как это показано на рис. 9.8 а, б.

В данных магнитных системах индукция в нейтральном сечении магнита не будет равна индукции в воздушном зазоре. На рис. 9.8,а В_d > В_m. На рис. 9.8,б В_d < В_m.

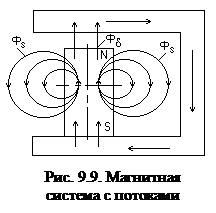
Все сказанное рассматривалось при малых потоках рассеяния. На рис. 9.9 показана магнитная система с потоками рассеяяния. Здесь индукция в нейтральном сечении магнита не равна индукции в воздушном зазоре.

Эти два фактора: неравенство площадей воздушного зазора и нейтрального сечения магнита и наличие потоков рассеяния не позволяют рассчитать поток или индукцию в воздушном зазоре оперируя значениями В и Н.

На рис. 9.9 видно, что через нейтральное сечение магнита проходят как поток Ф_d, так и поток Ф_s. Поэтому кривую размагничивания магнита целесообразно представлять в координатах Ф, F, a не в координатах В, Н, как на рис. 9.4, 9.7.

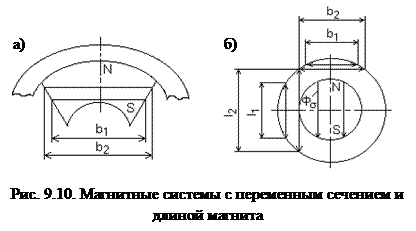Чтобы построить кривую размагничивания магнита в координатах Ф, F, (где Ф – магнитный поток в нейтральном сечении магнита, Вб, F – магнитодвижущая сила магнита, А) необходимо знать его геометрические размеры, в частности длину l_м и сечение S_м. На рис. 9.10 а, б показаны магнитные системы с переменной длиной и сечением.

Эквивалентные размеры магнитной системы рассчитываются индивидуально для каждой магнитной системы. Эти вопросы достаточно широко освящены в литературе. При известных длине и сечении текущие значения величин в осях Ф и F определяются

; ,

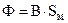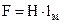где В – текущее значение индукции в нейтральном сечении магнита, Тл; Н – текущее значение напряженности в нейтральном сечении магнита, А/м; S_м – эквивалентное сечение магнита, м²; l_м – эквивалентная длина магнита, м.

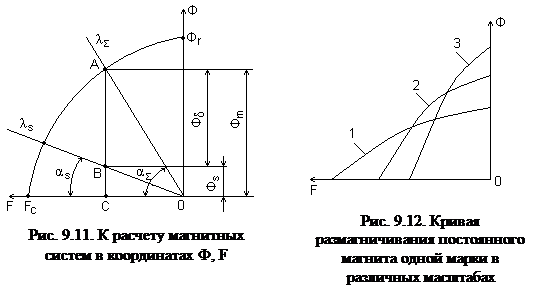Расчет магнитных систем сводится к следующему (рис. 9.11):

1. Строится кривая размагничивания постоянного магнита в координатах Ф, F.

2. Проводится луч суммарной проводимости l_å под углом a_å, где

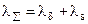, а , ,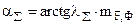

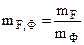где m_F – масштаб по оси F; m_Ф – масштаб по оси Ф.

В действительности кривая размагничивания может быть построена в различных масштабах, как это показано на рис. 9.12.

3. Проводится луч проводимости рассеяния l_s под углом a_s,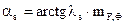

4. Из точки пересечения кривой размагничивания магнита А перпендикулярно оси F проводится отрезок АС. Суммарный магнитный поток в нейтральном сечении будет равен отрезку АС. Полезный поток в воздушном зазоре – отрезку АВ, поток рассеяния – отрезку ВС.