Равноточных измерений
Арифметическая средина результатов равноточных измерений. Пусть имеем результаты многократных равноточных измерений одной величины: l1, l2, …, ln. Рассмотрим их среднее арифметическое
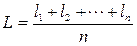 . (5.7)
. (5.7)
Из (5.1) следует li= Х + Δi (i = 1, 2, … n). Поэтому напишем
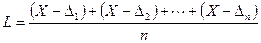 = X -
= X - 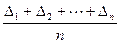 .
.
Согласно (5.2) с увеличением числа измерений сумма случайных погрешностей, деленная на их число, стремится к нулю, и, следовательно, среднее арифметическое L стремится к истинному значению Х. Поэтому значение определяемой величины принимают равным среднему арифметическому.
Средняя квадратическая погрешность арифметической средины. Пусть точность результатов измерений l1, l2, …, ln характеризуется средними квадратическими погрешностями
m1 = m2 = ¼ = mn = m
и требуется найти среднюю квадратическую погрешность M арифметической средины.
Представим формулу (5.7) в следующем виде:
L = 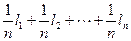 .
.
Среднюю квадратическую погрешность арифметической средины найдем как погрешность функции измеренных величин по формуле (5.6)
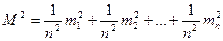
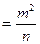
или 
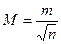 (5.8)
(5.8)
Формула (5.8) показывает, что погрешность арифметической средины с ростом числа измерений убывает пропорционально квадратному корню из этого числа. Так, чтобы погрешность среднего арифметического уменьшить в 2 раза, число измерений надо увеличить в 4 раза.
Обработка результатов равноточных измерений. Математическая обработка ряда результатов l1, l2, …, ln прямых равноточных измерений одной величины выполняется в следующей последовательности:
1. Вычисляют среднее арифметическое L
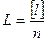 .
.
2. Вычисляют поправки к vi результатам измерений
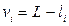 (i = 1, 2, …, n)
(i = 1, 2, …, n)
Контролем правильности вычислений служит сумма поправок, которая должна быть близка к нулю.
3. Вычисляют среднюю квадратическую погрешность одного измерения по формуле Бесселя:
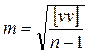 .
.
Значение m вычисляют с двумя-тремя значащими цифрами.
4. Вычисляют среднюю квадратическую погрешность среднего арифметического
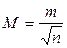 .
.
Дата добавления: 2016-09-26; просмотров: 2019;











