Коди з паралельною формою представлення інформації
У попередньому параграфі було розглянуто перетворення аналогового сигналу в послідовність сигналів, які умовно приймають лише значення “1” та “0”. Система числення, в якій використовуються лише два знаки для відображення інформації, називається двійковою, основою якої є число 2. За аналогією з десятковою, двійкова система числення є позиційною, і будь-яке ціле десяткове число може бути представлене двійковим рядом, що вміщує лише “1” та “0” у відповідності з алгоритмом:
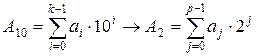 , (1.14)
, (1.14)
де аі = 0…9 – цифри і-го розряду десяткового числа; аj = 0…1 – відповідно, цифри j-го розряду двійкового числа. Розряди чисел рахуються зліва направо, починаючи зі старшого. Дробові числа представляються доповненням суми (1.14) від’ємними ступенями числа 2.
Електронні системи, що оперують сигналами, які відповідають лише рівням “1” та “0”, називаються цифровими. Схеми, на основі яких реалізуються такі системи, також називаються цифровими, а розділи електроніки, що вивчають принципи побудови таких схем – цифровою схемотехнікою.
Як у теорії інформації, так і на практиці застосування цифрової схемотехніки використовується багато різноманітних кодів. Визначимось з основною термінологією.
Код – це універсальний спосіб відображення інформації при її зберіганні, передачі і обробці у вигляді системи однозначних відповідностей між елементами повідомлень і сигналами, за допомогою яких ці елементи можна зафіксувати. Іншими словами, кодування – це однозначне перетворення символів одного алфавіту в символи іншого, а код – правило, закон, алгоритм, при якому відбувається це перетворення. Комбінації символів, що належать до даного коду, називаються кодовими словами. Символи, за допомогою яких повідомлення трансформується в код, є вторинним алфавітом. Процес відновлення вмісту повідомлення за допомогою відповідного коду називається декодуванням. Необхідною умовою декодування є взаємно однозначна відповідність кодових слів у вторинному алфавіті символам первинного алфавіту та їх комбінаціям. При передачі кодових символів по лініях зв’язку вони повинні бути розділені так, щоб кожен символ міг бути прийнятим самостійно, що виконується з використанням різних принципів їх розділення. Розділення символів може бути просторовим, часовим і якісним. Просторове розділення по суті є багатоканальним зв’язком, і при його використанні відпадає необхідність у спеціальних методах кодування. При якісному розділенні між символами повинно бути як мінімум дві розподільчі ознаки (наприклад, тривалість імпульсу, паузи), які легко відрізняються на приймальній стороні лінії зв’язку. Якісне розділення дає можливість одночасної передачі інформації від різних об’єктів по одному каналу зв’язку. Прикладом якісного розділення є частотне розділення (моногармонічний сигнал при імпульсі має одну частоту, а при паузі – іншу). При часовому розділенні використовуються спеціальні комутатори на передаючій та приймальній сторонах, які почергово з’єднують необхідні лінії зв’язку.
Двійкове кодування десяткових чисел в відповідності з (1.14) не є єдиним. При роботі з двійковими числами широко використовуються й інші коди, які в різних практичних ситуаціях мають свої переваги перед двійковим. Деякі з них для позитивних чисел в інтервалі 0…15 представлені у табл. 1.1.
Прямий двійковий код А2 також називають кодом 8-4-2-1 у вiдповiдностi з ваговими коефiцiєнтами розрядів.
Зворотній код B2 = b3 b2 b1 b0 отримується шляхом інверсії кожного розряду прямого коду:
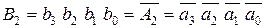 .
.
Таблиця 1.1.
| A10 | A2 (двійковий ) | B2 (зворотний) | D2 (доповнюючий) | Код Грея | ||||||||||||
| а 3 | a2 | a1 | a0 | b3 | b2 | b1 | b0 | d3 | d2 | d1 | d0 | g3 | g2 | g1 | g0 | |
Він використовується як самостійно в логічних структурах цифрових систем, так і при виконанні арифметичних операцій для одержання доповнюючого коду D2 . Останній застосовується при виконанні арифметичних операцій і знаходиться відповідно до формули:
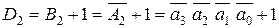 ,
,
де число 1 додається шляхом двійкової арифметики.
Код Грея, який часто називається циклічним, має ту особливість, що при переході з одного числа до сусіднього проходить зміна “0” на “1” або навпаки тільки в одному розряді. Як видно з таблиці, код, представлений двома, трьома або чотирма розрядами, завжди створює циклічну послідовність, тобто адекватну можливість переходу від самого старшого кодового значення числа до самого молодшого. Ця особливість дозволяє використовувати його при кодуванні кутових переміщень у перетворювачах кута повороту у цифровий код. Код Грея знаходить також широке використання у різних перетворювачах “аналог - код”, де його властивість дає можливість звести похибки неоднозначності при зчитуванні iнформацiї до одиниці молодшого розряду.
Для одержання коду Грея в літературі описані декілька різних прийомів. Один з них дозволяє будувати код Грея безпосередньо з двійкового, використовуючи наступне правило: і-й біт коду Грея встановлюється в нуль, якщо і-й та (і + 1)-й біти відповідного двійкового коду однакові; у протилежному випадку біт і = 1. У тому випадку, коли (і + 1)-й біт виходить за рамки розрядності двійкового коду, його значення приймається рівним нулю.
При записi слiв двiйкового коду може використовуватись шiстнадцяткове числення:
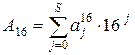 .
.
При його використанні десяткові числа від 10 до 15 замінюються вiдповiдно латинськими лiтерами A, B, C, D, E, F. Двiйковий i шiстнадцятковий коди легко взаємно переводяться. Для цього двiйкове слово будь-якої довжини розбивається на тетради, починаючи з молодшого розряду i, вiдповiдно до табл. 1.1 та вищезазначеними еквiвалентами лiтер та цифр, записується його шiстнадцяткове представлення. Наприклад,
A2 = 1110112 = 0011 10112 = 3B16 .
Для позначення цього коду використовують букву h (hexadecimal), яку ставлять після його числового значення: 3B16 = 3Bh.
У задачах обчислювальної та мiкропроцесорної технiки часто виникає необхiднiсть працювати з десятковими числами. Для цього використовують двiйкове представлення кожної десяткової цифри окремо у відповідності з табл. 1.2. Наприклад, числу 93710 вiдповiдає код 1001 0011 0111. Таке представлення називається двiйково-десятковим кодом. При виконанні арифметичних операцій з використанням двiйково-десяткового коду виникають проблеми, пов’язані із переносом з одного розряду до іншого. Для їх вирішення використовуються самодоповнюючi коди. До них відносяться код Айкена, вагові коефіцієнти розрядів якого2-4-2-1,а такожкод“з надлишком 3”, якийотримується з двiйково-десяткового шляхом додавання числа 3. Особливості цих кодів можна побачити з табл. 1.2.
Таблиця 1.2.
| Десяткове число | Двійково-десятковий код | Код Айкена 2-4-2-1 | Код “з надлишком 3” | |||||||||
| A10 | a3 | a2 | a1 | a0 | h3 | h2 | h1 | h0 | c3 | c2 | c1 | c0 |
Розглянемо більш детально взаємозв’язок мiж кодами на прикладi конкретних чисел. Для числа 3, представленого в кодi “з надлишком 3”, у відповідності до табл. 1.2, маємо:
C = с3 с2 с1 с0 = 0110 = 310; 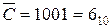 .
.
В результатi 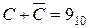 .
.
Аналогiчно в коді Айкена вiзьмемо число 510 . З табл.1.2
H = h3 h2 h1 h0 = 1011.
Вiдповiдно
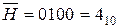 .
.
В результатi 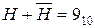 .
.
Бачимо, що властивістю самодоповнюючих кодів є те, що їх зворотні комбінації доповнюють прямі до 9. Ця особливiсть дозволяє мiкропроцесорним пристроям виконувати арифметичнi операцiї з десятковими числами.
У мікропроцесорній техніці двійково-десяткові коди широко використовуються для відображення цифрової інформації за допомогою знакосинтезуючих індикаторів. Тому необхідно вміти виконувати перетворення двійкового коду будь-якої розрядності у двійково-десятковий. Виконується ця операція у такій послідовності. Оскільки, наприклад, однобайтовим двійковим словом може бути закодована цифра, яка у десятковому коді містить три знаки (до 255), то таке слово повинно бути переміщене з двійкового регістру R відповідними засобами у три чотирьохбітні регістри – регістр одиниць RО , регістр десятків RД і регістр сотень RС :
RС RД RO R .
Виходячи з правил двійкової арифметики, при переміщенні кожного розряду з регістра R у регістри, розміщені зліва, необхідно контролювати значення чисел, що з’являються в регістрах RС , RД , RО .
Якщо ці числа дорівнюють або перевищують 510 = 01012 , то до них необхідно додати число 310 = 00112 .
Контролюючи у такий спосіб вміст кожного регістра, за вісім тактів операції зсуву виконується повний цикл перетворення двійкового числа з регістру R у відповідні регістри RС , RД , RО .
Читачам пропонується самостійно поекспериментувати над таким перетворенням.
Приклад 1.9. Виконати перетворення числа 21710 = 1101 10012 у двійково-десятковий код шляхом використання операцій зсуву та додавання числа 310 .
Розв’язання. Керуючись алгоритмом, описаним вище, виконуємо відповідне перетворення.
| № етапу | Регістр сотень RC | Регістр десятків RД | Регістр одиниць RО | Задане число, регістр R | ||||||||||||||||||||
| 210 | 110 | 710 |
Двiйковi коди використовуються не тiльки для кодування цифрової iнформації. Широко вiдоме двiйкове представлення букв, знакiв, типових команд. У вiтчизнянiй практицi такий код називається КОI-7 (код для обмiну iнформацiєю, семирозрядний). Аналогiчний код використовується в сучаснiй комп’ютерний техніці, який називається ASCII (American Standart Code for Information Interchange) і достатньо детально описаний у рядi лiтературних джерел.
Передача iнформацiї завжди пов’язана з імовірністю появи похибок у лiнiї зв’язку. Вони пов’язанi з тим, що при передачi iнформацiї в двiйковому кодi окремi дискретнi символи “0” та “1” можуть змiнюватись вiдповiдно на “1” та “0” при дiї перешкод. Тому на практиці широко використовуются коди, які називаються коригуючими або перешкодозахищеними. Вони дозволяють своєчасно виявляти i виправляти похибки, що з’являються. Побудова таких кодiв завжди пов’язана із введенням надмiрностi у лiнiю зв’язку та кодовi комбiнацiї, що передаються. Найпростiшим з перешкодозахищених кодiв є двiйковий код з забезпеченням можливостi перевiрки на парнiсть, у якому до n-розрядного коду, що передається, додається допомiжний (n + 1)-й розряд. Детально його використання описується в третьому розділі. Недолік такого коду полягає у відсутності можливості автоматично ліквідовувати похибки. Незважаючи на це, він широко використовується в ЕОМ при роботі процесора з запам’ятовуючими пристроями.
До кодів, що виправляють можливі похибки, відносяться циклічні коди, які мають можливість виявляти та виправляти не тільки одиночні, а й похибки більшої кратності. До таких кодів відноситься код Ріда-Соломона, який широко використовується захисту інформації в комп’ютерних системах.
Дата добавления: 2016-09-26; просмотров: 2108;











