Расчет прочности по нормальным сечениям
Элементы прямоугольного сечения с одиночной арматурой. Расчет изгибаемых элементов по нормальным сечениям производится по стадии III напряженно-деформированного состояния. Для получения расчетных зависимостей проведем в балке (рис. 4.3, а) сечение, отбросим правую часть и заменим ее действие внутренними силами. Так как действительные законы распределения напряжений по сечению достаточно сложны, то принимают упрощающие предпосылки: 1) напряжения в бетоне в предельном состоянии принимают равными расчетному сопротивлению Rb; 2) действительная криволинейная эпюра напряжений в бетоне сжатой зоны заменяется прямоугольной; применение такой эпюры в качестве расчетной приводит к погрешностям, не превышающим 2...8%, но позволяет упростить расчетные зависимости; 3) усилиями, воспринимаемыми растянутым бетоном над устьем трещины, пренебрегают вследствие их малости.
Прочность сечения элемента будет обеспечена, если расчетный момент от внешней нагрузки не превысит расчетного момента внутренних усилий относительно центра тяжести сечения растянутой арматуры (рис. 4.3 б):
M ≤ Nb(ho – x/2) = Rbbx (ho – x/2) (4.1)
или относительно центра тяжести сжатой зоны бетона
M ≤ Ns(ho – x/2) = σs As (ho – x/2) (4.2)
где ho – рабочая высота сечения, ho = h – a; a - расстояние от растянутой грани сечения до центра тяжести арматуры: в плитах а = 1,5...2 см, в балках (при расположении арматуры в один ряд) а = 3...4 см; х — высота сжатой зоны бетона, определяемая из условия равенства нулю суммы проекций всех сил на продольную ось элемента (рис. 4.3,б):
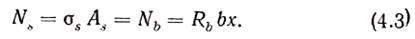
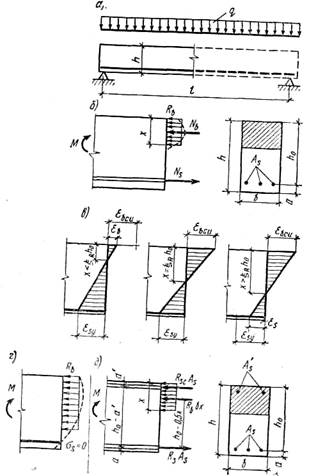
Рис. 4.3. К расчету сечений с одиночной (а, б, в, г) и двойной (д) арматурой;
к определению граничной высоты сжатой зоны (в)
Входящие в формулы (4.2), (4.3) напряжения в растянутой арматуре σs определяются характером разрушения, зависят от содержания арматуры в сечении, высоты сжатой зоны и т. п. и находятся по эмпирической формуле
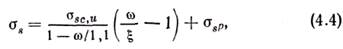
где ω — параметр, характеризующий условную высоту прямоугольной эпюры сжатой зоны бетона, при которой фактическая нейтральная ось проходит через центр тяжести растянутой арматуры (рис. 4.3, г), ω = 0,85—0,008 Rb; ξ = x/ho — относительная высота сжатой зоны; σsc,u — предельные напряжения в арматуре сжатой зоны, принимаемые при γb2 ≥ 1 — 400 МПа, при γb2 ≥ 1 — 500 МПа; σsp — предварительное напряжение в арматуре с учетом всех потерь и γsp < l.
Разрушение сечения (см. § 2.2) может произойти либо вследствие достижения в растянутой арматуре предела текучести (физического или условного) σs = Rs и последующего разрушения бетона сжатой зоны (случай 1), либо вследствие разрушения бетона сжатой зоны при напряжениях в арматуре, меньших предела текучести σs < Rs (случай 2). Поэтому прежде всего необходимо установить условия, которые позволили бы расчетным путем определить, по какому случаю будет работать сечение. Для установления этих условий рассмотрим рис. 4.3, в, на котором изображены деформации бетона εb, соответствующие достижению деформаций текучести арматуры εsy = Rs/Es, а также высота сжатой зоны х при различном содержании арматуры в сечении. Из рисунка видно, что при небольшой As x невелик, деформации арматуры достигают текучести ранее, чем деформации бетона при сжатии достигают своих предельных значений εbcu, т. е. имеет место случай 1. С увеличением содержания арматуры растут высота и деформации бетона сжатой зоны. При определенном x=xR деформации бетона станут равными предельным значениям εbcu и разрушение бетона наступит одновременно с текучестью арматуры.
Очевидно, это состояние и будет границей между случаями 1 и 2. При больших As и x>xR разрушение произойдет по сжатому бетону (случай 2). В расчетной практике для установления границы используют не х, а относительную высоту сжатой зоны ξ=х/h0, которая характеризует основные параметры конструкции (классы бетона, арматуры, площадь сечения арматуры, бетона) и особенности напряженно-деформированного состояния. Значению xR соответствует граничное значение относительной высоты сжатой зоны, определяемое по формуле (4.5), полученной на основе формулы (4.4):
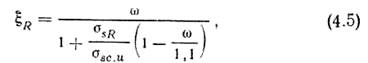
где σsR — напряжение в арматуре: для арматуры классов A-I, А-II, A-III, Bp-I σsR=Rs; для предварительно напряженной арматуры классов A-IV и выше σsR=Rs+400-σsp-Δσsp, здесь Δσsp — коэффициент, зависящий от класса арматуры и способа натяжения [1].
Таким образом, при ξ≤ξR расчет элементов следует производить по случаю 1, при ξ>ξR — по случаю 2.
● Случай 1 (ξ≤ξR). С учетом вышеизложенного формулы (4.1)...(4.3) примут такой вид:
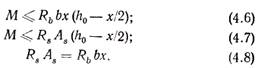
Из формулы (4.8) высота сжатой зоны

Относительная высота сжатой зоны
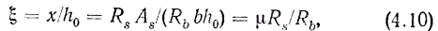
где μ=As/(bh0)—коэффициент армирования. В расчетной практике часто используют также понятие «процент армирования» μ% = μ100%.
Пользуясь полученными формулами, можно решать задачи расчета сечений. Для упрощения практических расчетов формулы преобразуют, вводя параметры αm и ζ. Подставив в формулу (4.6) x = ξh0, получим
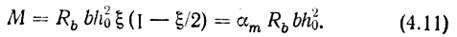
Откуда
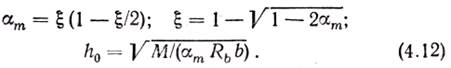
Аналогично, преобразуя уравнение (4.7), будем иметь
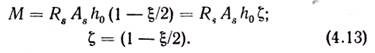
Откуда

Полученные формулы справедливы при
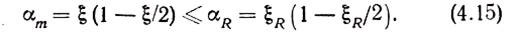
Величины ξ, αm и ζ взаимно связаны друг с другом. Зная одну из них или задаваясь одной из них, можно с помощью табл. 4.1 найти любую другую.
Одинаковую несущую способность можно обеспечить при различных размерах сечения и соответственно разных процентах армирования. Так, с увеличением высоты сечения можно уменьшить количество арматуры и наоборот. При проектировании следует исходить из наиболее экономичных решений, для которых стоимость конструкций будет наименьшей. Исследования показывают, что экономичные решения будут получены при ξ=0,25...0,4 для балок и ξ = 0,1...0,2 для плит. Максимальное значение коэффициента армирования, при котором сечение будет работать по случаю 1, получим, подставляя граничное значение высоты сжатой зоны ξR в формулу (4.10), откуда μmax = ξRRb/Rs.
Для железобетонных изгибаемых элементов из бетона классов В12,5...В30, армированных сталями классов А-II, А-III, Вр-I, μmax=1,3...3,2 %.
Нормы ограничивают и минимальный процент армирования, назначаемый из условия равнопрочности армированного и неармированного сечений. Для изгибаемых элементов μmin=0,05 %. Если процент армирования элемента ниже указанного минимума, то расчет следует производить без учета арматуры, т. е. как неармированного бетонного элемента.
В последнем случае прочность элемента из тяжелого бетона рассчитывается по формуле

Таблица 4.1.
Значения коэффициентов ξ, ζ, и αm для расчетов
изгибаемости элементов прямоугольного сечении
| ξ | ζ | αm | ξ | ζ | αm |
| 0,01 | 0,995 | 0,01 | 0,36 | 0,82 | 0,295 |
| 0,02 | 0,99 | 0,02 | 0,37 | 0,815 | 0,301 |
| 0,03 | 0,985 | 0,03 | 0,38 | 0,81 | 0,309 |
| 0,04 | 0,98 | 0,039 | 0,39 | 0,805 | 0,314 |
| 0,05 | 0,975 | 0,048 | 0,4 | 0,8 | 0,32 |
| 0,06 | 0,97 | 0,058 | 0,41 | 0,795 | 0,326 |
| 0,07 | 0,965 | 0,067 | 0,42 | 0,79 | 0,332 |
| 0,08 | 0,96 | 0,077 | 0,43 | 0,785 | 0,337 |
| 0,09 | 0,955 | 0,085 | 0,44 | 0,78 | 0,343 |
| 0,1 | 0,95 | 0,095 | 0,45 | 0,775 | 0,349 |
| 0,11 | 0,945 | 0,104 | 0,46 | 0,77 | 0,354 |
| 0,12 | 0,94 | 0,113 | 0,47 | 0,765 | 0,359 |
| 0,13 | 0,935 | 0,121 | 0,48 | 0,76 | 0,365 |
| 0,14 | 0,93 | 0,13 | 0,49 | 0,755 | 0,37 |
| 0,15 | 0,925 | 0,139 | 0,5 | 0,75 | 0,375 |
| 0,16 | 0,92 | 0,147 | 0,51 | 0,745 | 0,38 |
| 0,17 | 0,915 | 0,155 | 0,52 | 0,74 | 0,385 |
| 0,18 | 0,91 | 0,164 | 0,53 | 0,735 | 0,39 |
| 0,19 | 0,905 | 0,172 | 0,54 | 0,73 | 0,394 |
| 0,20 | 0,9 | 0,18 | 0,55 | 0,725 | 0,399 |
| 0,21 | 0,895 | 0,188 | 0,56 | 0,72 | 0,403 |
| 0,22 | 0,89 | 0,196 | 0,57 | 0,715 | 0,408 |
| 0,23 | 0,885 | 0,203 | 0,58 | 0,71 | 0,412 |
| 0,24 | 0,88 | 0,211 | 0,59 | 0,705 | 0,416 |
| 0,25 | 0,875 | 0,219 | 0,6 | 0,7 | 0,42 |
| 0,26 | 0,87 | 0,226 | 0,61 | 0,695 | 0,424 |
| 0,27 | 0,865 | 0,236 | 0,62 | 0,69 | 0,428 |
| 0,28 | 0,86 | 0,241 | 0,63 | 0,685 | 0,432 |
| 0,29 | 0,855 | 0,248 | 0,64 | 0,68 | 0,435 |
| 0,30 | 0,85 | 0,255 | 0,65 | 0,675 | 0,439 |
| 0,31 | 0,845 | 0,262 | 0,66 | 0,67 | 0,442 |
| 0,32 | 0,84 | 0,269 | 0,67 | 0,665 | 0,446 |
| 0,33 | 0,835 | 0,275 | 0,68 | 0,66 | 0,449 |
| 0,34 | 0,83 | 0,282 | 0,69 | 0,655 | 0,452 |
| 0,35 | 0,825 | 0,289 | 0,7 | 0,65 | 0,455 |
где Wpl — упругопластический момент сопротивления бетонного сечения; для элементов прямоугольного профиля Wpl = bh2/3,5[l].
При расчете сечений встречаются со следующими основными задачами: определение площади растянутой арматуры As; подбор размеров поперечного сечения элемента b и h и арматуры As; проверка несущей способности сечения. При проверке несущей способности определяют х из (4.9) и подставляют его значение в (4.6) или (4.7). При расчете As из (4.11) находят αm, затем по табл. 4.1 определяют ξ и по (4.14) вычисляют As. Блок-схемы решения указанных задач приведены в приложениях.
● Случай 2 (ξ>ξR). При расчете используют условия (4.1)...(4.3). Расчет элементов из бетона классов В30 и ниже с ненапрягаемой арматурой классов A-I, A-II, А-III при x>ξRh0 допускается производить по формулам случая 1, подставляя в них x= ξRh0. В этом случае момент, воспринимаемый прямоугольным сечением с одиночной арматурой, будет
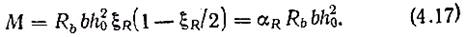
Элементы с избыточным содержанием арматуры — «переармированные» (ξ>ξR) — экономически невыгодны, так как прочностные свойства арматуры используются не полностью и это приводит к перерасходу стали. Поэтому изгибаемые элементы следует проектировать так, чтобы соблюдалось условие x ≤ ξRh0.
■ Элементы прямоугольного сечения с двойной арматурой. Сечениями с двойной арматурой называют такие, в которых кроме растянутой арматуры ставится по расчету сжатая. Необходимость в сжатой арматуре возникает, когда сечение с одиночной арматурой не может воспринять расчетный момент от внешней нагрузки вследствие недостаточной прочности бетона сжатой зоны (разрушение по случаю 2). Чтобы сжатая зона в таких конструкциях восприняла все сжимающие усилия, ее необходимо усилить арматурой. Сечения с двойной арматурой неэкономичны по расходу стали, так как увеличивается расход продольной арматуры и требуется постановка поперечных стержней (с шагом не более 15d в вязаных каркасах и 20d — в сварных), обеспечивающих закрепление сжатых рабочих продольных стержней от выпучивания. Поэтому сжатую арматуру ставят по расчету только в особых случаях: при ограниченных размерах поперечного сечения элемента; невозможности повышения класса бетона; при действии изгибающих моментов двух знаков или других специальных требованиях.
Формулы для расчета нормальных сечений элементов с двойной арматурой получены из тех же условий, что и для элементов с одиночной. В соответствии с расчетной схемой (рис. 4.3, д) условие прочности изгибаемого элемента в предельном состоянии имеет вид
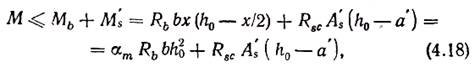
а уравнение проекций всех сил на горизонтальную ось
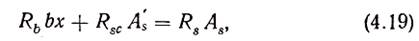
где Мb — момент, воспринимаемый сжатой зоной бетона и соответствующей частью растянутой арматуры; M's — момент, воспринимаемый сжатой арматурой A's и соответствующей частью растянутой.
При расчете сечений элементов с двойной арматурой могут встретиться два типа задач: 1) сжатая арматура необходима для усиления сжатой зоны бетона (если увеличение размеров сечения нежелательно) и 2) сжатая арматура предусмотрена по конструктивным соображениям или при условии действия изгибающих моментов двух знаков. При решении задач первого типа в двух исходных уравнениях (4.18) и (4.19) оказывается три неизвестных х, As, A′s. Вследствие этого принимается дополнительное условие, которое отвечает экономическим требованиям.
Исследования показывают, что сечение будет наиболее экономичным, когда на бетон передается максимально возможное сжимающее усилие. Это будет иметь место при ξ = ξR. В этом случае сжатая арматура воспримет момент M's=RscA's(h0—a') = M—αRRbbh  , откуда A's = (М—αRRbbh
, откуда A's = (М—αRRbbh  )/[Rsc(h0-а')]. Площадь растянутой арматуры As получают из условия (4.19), принимая х = xR = ξRh0: As=RscA's/Rs+RbξRbh0/Rs.
)/[Rsc(h0-а')]. Площадь растянутой арматуры As получают из условия (4.19), принимая х = xR = ξRh0: As=RscA's/Rs+RbξRbh0/Rs.
Блок-схемы решения указанных задач приведены в приложениях.
Проверка несущей способности осуществляется по условию (4.18), при этом х находится из формулы (4.19).
Формулами (4.18)...(4.19) можно пользоваться при х≥1,1а'. В противном случае сжатая арматура окажется вблизи нейтральной оси и напряжения в ней будут ниже Rsc.
■ Элементы таврового профиля. В первый период применения железобетона перекрытия сооружений выполнялись в виде сплошных плит. Однако такие конструкции нерациональны, поскольку сжатая зона составляет 1/10…1/5 их высоты, а растянутая зона сечения бетона в расчете прочности не учитывается и служит для размещения арматуры (рис. 4.4, а). Если часть бетона из растянутой зоны удалить, оставив его только вблизи арматурных стержней, сведенных в группы, то получится ребристая плита (рис. 4.4, б). Несущая способность плиты при этом не изменится, а расход бетона и вес конструкции значительно уменьшатся. Такие элементы, называемые тавровыми, широко применяются в виде отдельных балок, настилов, в составе монолитных ребристых перекрытий и т. п.
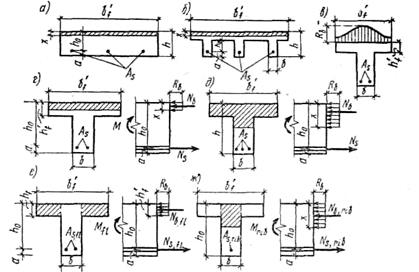
Рис. 4.4. К расчету тавровых сечений
Опыты показывают, что полка (рис. 4.4, в) вовлекается в совместную работу с ребром сдвигающими усилиями, и на участках, удаленных от ребра, напряжения будут меньше. Это учитывается условным уменьшением вводимой в расчет ширины свесов. Например, для отдельных балок таврового сечения с консольными свесами вводимая в расчет ширина полки должна составлять [1]:
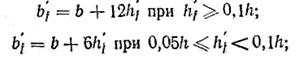
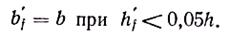
При расчете балок таврового сечения различают два случая: сжатая зона бетона находится в пределах полки (рис. 4.4, г) или ниже полки (рис. 4.4, д).
●Случай 1 (x>h'f) обычно встречается в сечениях с развитой полкой, когда внешний расчетный момент меньше внутреннего момента, воспринимаемого сжатой полкой сечения относительно центра тяжести арматуры:
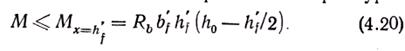
Тавровые сечения этого типа рассчитывают как прямоугольные с размерами b′f и h, поскольку площадь растянутого бетона не влияет на несущую способность. Для расчета используют формулы (4.6)...(4.9), полученные ранее для прямоугольного сечения с одиночной арматурой, в которых b заменяют на b'f. При относительно тонкой полке (h'f ≤ 0,2h) можно принять x=h'f и для определения площади арматуры пользоваться приближенной формулой
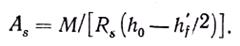
Коэффициент армирования для сечений, рассчитываемых по 1-му случаю, принимают μ=As/(bh0).
●Случай 2 (x>h'f) имеет место, если внешний расчетный момент будет больше внутреннего момента, воспринимаемого только сжатой полкой. Тавровые сечения этого типа встречаются при расчете балочных конструкций с малой шириной свесов полки.
Для получения расчетных зависимостей изгибающий момент, воспринимаемый сечением (рис. 4.4, д), разделяют на два заменяющих момента: Мfl (рис. 4.4, е), воспринимаемый свесами полок и соответствующей арматурой As,fl, и момент Мrib (рис. 4.4, ж), воспринимаемый сжатым бетоном ребра и соответствующей ему арматурой As,rib: M=Mfl+Mrib. Тогда из рис. 4.4, е
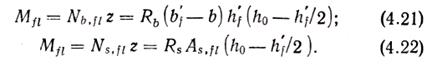
Определив Мfl по формуле (4.21), из формулы (4.22)
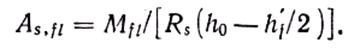
При известных М и Мfl площадь сечения арматуры подбирают как для обычного прямоугольного сечения шириной b на действие момента Mrib=M—Mfl: определяют αm=Mrib/(Rbbh 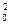 ), затем по табл. 4.1 находят соответствующее значение ζ, тогда
), затем по табл. 4.1 находят соответствующее значение ζ, тогда
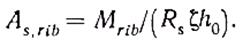
Общая площадь продольной рабочей арматуры в тавровом сечении
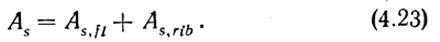
Блок-схема расчета таврового сечения приведена в приложениях.
●Элементы, прямоугольного сечения, армированные напрягаемой и ненапрягаемой арматурой (смешанное армирование). Расчет прочности производят по III стадии напряженно-деформированного состояния, случаю 1 (ξ≤ξR). Предполагают, что напрягаемая арматура принята из высокопрочной стали, а ненапрягаемая — из мягких арматурных сталей с физическим пределом текучести. Рассматривая усилия, действующие в сечении (рис. 4.5, а), получают условие прочности. Для этого составляют уравнение моментов всех сил относительно центра тяжести растянутой арматуры
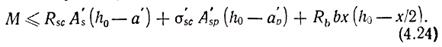
Положение нейтральной оси определяют из уравнения Σy=0:
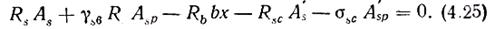
Предполагают, что напряжения в бетоне и ненапрягаемой арматуре в предельном состоянии достигают расчетных значений Rb, Rs и Rsc. Напряжения в растянутой напрягаемой арматуре, не имеющей физического предела текучести, определяют произведением γs6Rs, где γs6 — коэффициент условий работы
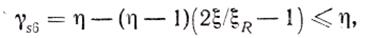
здесь η — коэффициент, принимаемый равным для арматуры классов A-IV—1,2, A-V, B-II, К-7—1,15, A-VI—1,10.
Необходимость введения коэффициента γs6 обусловлена тем, что при достижении в арматуре напряжений σ0,2 (если ξ≤ξR) бетон сжатой зоны, как показывают опыты, не разрушается. При увеличении внешней нагрузки до значения, при котором разрушается бетон, удлинения растянутой арматуры возрастают, что приводит к росту в ней напряжений. Это явление не наблюдается в элементах, армированных сталями, имеющими физический предел текучести. Повышение напряжений зависит от характера диаграммы растяжения стали и величины ξ. С уменьшением ξ деформации растянутой арматуры к моменту разрушения сжатой зоны увеличиваются, напряжения в арматуре, не имеющей площадки текучести, повышаются.
Если в качестве ненапрягаемой арматуры As используют высокопрочную сталь, то в предельном состоянии напряжения в ней могут достичь расчетного сопротивления или быть ниже его значения в зависимости от величин ξ, σsp и соотношения классов напрягаемой и ненапрягаемой арматуры. Как показывают исследования, напряжения в ненапрягаемой арматуре, принятой одного класса с напрягаемой, достигают значения Rs при ξ≤0,5ξR и относительно невысокой степени предварительного напряжения арматуры Asp.
Напряжения в арматуре A'sp
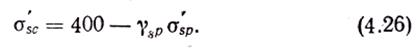
Формула выражает тот факт, что до приложения внешней нагрузки в арматуре A'sp действует растягивающее предварительное напряжение σ'sp (c учетом потерь и коэффициента точности натяжения γsp>l). Внешняя нагрузка вызывает сжимающие напряжения, предельные значения которых при коэффициенте условий работы бетона γb2≥1 составляют 400 МПа, а при γb2<1 — 500 МПа. Если γspσ′sp<400 (или 500), арматура A′sp будет сжата (σ′sc>0), при γspσ′sp>400 (или 500) предварительное напряжение не будет погашено (σ′sp <0) и арматура останется растянутой, действуя на сечение как внешняя обжимающая сила.
●Элементы с несущей (жесткой) арматурой. Изгибаемые элементы с несущей арматурой применяют в монолитных сооружениях. В этом случае можно исключить устройство лесов, а опалубку подвешивать непосредственно к арматуре. Во время возведения сооружения несущая арматура работает как металлическая конструкция на нагрузки от массы опалубки, бетона и т. п. После приобретения бетоном необходимой прочности конструкции с несущей арматурой работают как железобетонные и воспринимают эксплуатационные нагрузки. Сечение несущей арматуры, по экономическим соображениям, принимают наименьшим возможным из расчета на монтажные нагрузки. При расчете на эксплуатационные нагрузки в железобетонном сечении при необходимости может быть добавлена продольная гибкая рабочая арматура.
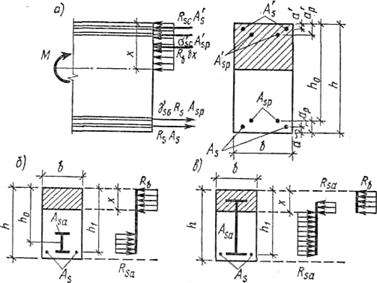
Рис. 4.5. Схема усилий в сечении элемента с обычной и напрягаемой арматурой при расчете прочности (а); к расчету прочности изгибаемых элементов с жесткой арматурой (б, в)
Опыты показали, что жесткая арматура работает совместно с бетоном вплоть до разрушения. При этом прочность бетона и арматуры используется полностью. Принципы расчета прочности изгибаемых элементов с жесткой арматурой не отличаются от расчета обычных железобетонных элементов. В практике проектирования встречаются два случая.
●Случай 1 — нейтральная ось расположена выше жесткой арматуры (рис. 4.5, б). Эпюры напряжений в сжатом бетоне и растянутой арматуре прямоугольные. Условия прочности получают, составив уравнение моментов всех сил, действующих в сечении, относительно нейтральной оси
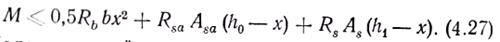
Положение нейтральной оси определяют из условия равновесия
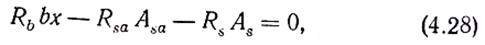
где Rsa — расчетное сопротивление жесткой арматуры; Asa — площадь поперечного сечения жесткой арматуры.
●Случай 2 — нейтральная ось пересекает стенку профиля жесткой арматуры (рис. 4.5, в). Условия прочности и уравнение для определения положения нейтральной оси получают аналогично предыдущему.
Дата добавления: 2019-05-21; просмотров: 2069;











