Глава 2. Действия над матрицами
Сумма двух матриц  и
и 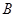 одинаковых размеров определяется как матрица
одинаковых размеров определяется как матрица 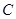 тех же размеров, каждый элемент которой равен сумме соответствующих элементов матриц, т. е.
тех же размеров, каждый элемент которой равен сумме соответствующих элементов матриц, т. е. 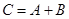 , если
, если 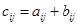 . Пусть, например,
. Пусть, например, 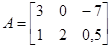 и
и 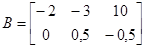 , тогда
, тогда 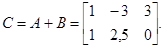
Из приведенного определения следует, что операция сложения матриц коммутативна, т. е. 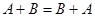 , и ассоциативна, т. е.
, и ассоциативна, т. е. 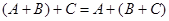 . Она естественным образом распространяется на любое число слагаемых. Очевидно также, что матрица
. Она естественным образом распространяется на любое число слагаемых. Очевидно также, что матрица  не изменяется при суммировании ее с нулевой матрицей тех же размеров, т. е.
не изменяется при суммировании ее с нулевой матрицей тех же размеров, т. е. 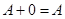 .
.
По определению произведением матрицы  на число
на число 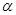 (скаляр) является матрица
(скаляр) является матрица 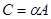 , элементы которой получаются умножением соответствующих элементов матрицы
, элементы которой получаются умножением соответствующих элементов матрицы  на это число
на это число 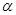 , т. е.
, т. е. 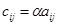 .
.
Очевидно, справедливы следующие соотношения: 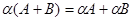 ;
; 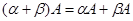 ;
; 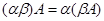 , где
, где  и
и 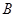 –
матрицы одинакового размера;
–
матрицы одинакового размера; 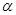 и
и 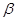 – числа (скаляры). Общий множитель элементов можно выносить за знак матрицы, считая его скалярным множителем.
– числа (скаляры). Общий множитель элементов можно выносить за знак матрицы, считая его скалярным множителем.
Разность двух матриц одинаковых размеров сводится к уже рассмотренным операциям соотношением 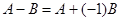 , т. е.
, т. е. 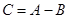 , если
, если 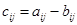 .
.
Множество всех прямоугольных матриц одинакового размера 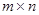 образует линейное пространство над числовым полем с внутренней операцией – сложением матриц и внешней операцией – умножением матрицы на число.
образует линейное пространство над числовым полем с внутренней операцией – сложением матриц и внешней операцией – умножением матрицы на число.
Произведением матрицы  размера (
размера ( 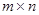 ) на матрицу
) на матрицу 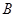 размера (
размера ( 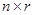 ) является матрица
) является матрица 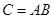 размера (
размера ( 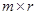 ), элемент
), элемент 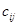 которой, расположенный в
которой, расположенный в 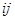 -клетке, равен сумме произведений элементов
-клетке, равен сумме произведений элементов 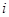 -й строки матрицы
-й строки матрицы  на соответствующие элементы
на соответствующие элементы 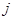 -го столбца матрицы
-го столбца матрицы 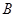 , т. е.
, т. е.
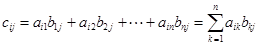 .
.
Умножение  на
на 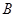 допустимо (произведение
допустимо (произведение 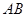 существует), если число столбцов
существует), если число столбцов  равно числу строк
равно числу строк 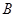 , т. е. эти две матрицы согласуются по форме.
, т. е. эти две матрицы согласуются по форме.
При выполнении операции умножения матриц по рассмотренному правилу удобно пользоваться схемой, приведенной на рис. 1
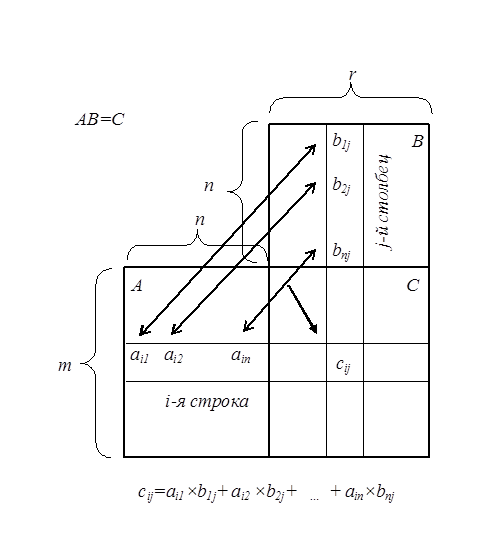
|
| Рис. 1 |
На рис. 2 показаны схемы для типичных случаев умножения матриц. В результате умножения двух матриц получается также матрица (рис. 2а). Произведение матрицы на столбец дает столбец (рис. 2б), а строки на матрицу–строку (рис. 2в). При умножении строки на столбец получается матрица с единственным элементом (рис. 2г), которая отождествляется с этим элементом. В случае умножения столбца на строку получается матрица (рис. 2д).
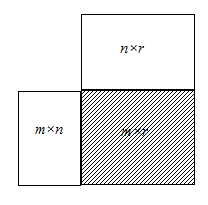
| 
| 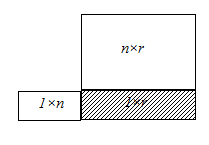
|
| а | б | в |
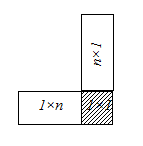
| 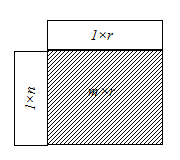
| |
| г | д | |
| Рис. 2 |
Для матриц 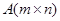 и
и 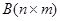 существует как произведение
существует как произведение 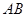 размера m×m, так и произведение
размера m×m, так и произведение 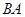 размера n×n.
Ясно, что при
размера n×n.
Ясно, что при 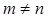 эти произведения не могут быть равными уже вследствие различных размеров результирующих матриц. Но даже при
эти произведения не могут быть равными уже вследствие различных размеров результирующих матриц. Но даже при 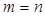 , т. е. в случае квадратных матриц одинакового порядка, произведения
, т. е. в случае квадратных матриц одинакового порядка, произведения 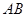 и
и 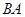 не обязательно равны между собой. Например, для матриц
не обязательно равны между собой. Например, для матриц 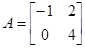 и
и 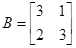 произведение
произведение 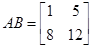 , а произведение
, а произведение 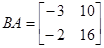 .
.
Отсюда следует, что операция умножения матриц не подчиняется коммутативному закону ( 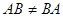 ). Если выполняется соотношение
). Если выполняется соотношение 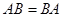 , то матрицы
, то матрицы  и
и 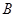 называют коммутирующими. Ассоциативный и дистрибутивный законы для матричного умножения выполняются во всех случаях, когда размеры матриц допускают соответствующие операции:
называют коммутирующими. Ассоциативный и дистрибутивный законы для матричного умножения выполняются во всех случаях, когда размеры матриц допускают соответствующие операции: 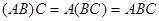 (ассоциативность),
(ассоциативность), 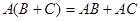 и
и 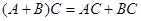 (дистрибутивность умножения слева и справа относительно сложения).
(дистрибутивность умножения слева и справа относительно сложения).
Умножение матрицы 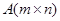 на единичную матрицу
на единичную матрицу 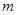 -го порядка слева и на единичную матрицу
-го порядка слева и на единичную матрицу 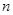 -го порядка справа не изменяет этой матрицы, т. е.
-го порядка справа не изменяет этой матрицы, т. е. 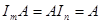 .
.
Если хотя бы одна из матриц произведения 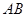 является нулевой, то в результате получается нулевая матрица. Однако, из
является нулевой, то в результате получается нулевая матрица. Однако, из 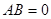 не обязательно следует, что
не обязательно следует, что 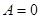 или
или 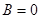 . В этом можно убедиться на следующем примере. Пусть
. В этом можно убедиться на следующем примере. Пусть
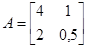 и
и 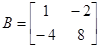 . Тогда
. Тогда 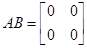 .
.
Произведения одинаковых квадратных матриц  можно записать как ее степень
можно записать как ее степень 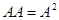 ,
, 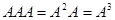 и т. д. Как и для чисел имеют место обычные свойства:
и т. д. Как и для чисел имеют место обычные свойства: 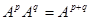 ,
, 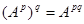 ,где
,где 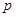 и
и 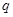 – положительные числа для произвольной квадратной матрицы и любые целые числа (положительные, отрицательные и нуль) для неособенной матрицы. В частности,
– положительные числа для произвольной квадратной матрицы и любые целые числа (положительные, отрицательные и нуль) для неособенной матрицы. В частности, 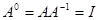 .Никакая степень числа, отличного от нуля, не может равняться нулю. В то же время степень квадратной матрицы
.Никакая степень числа, отличного от нуля, не может равняться нулю. В то же время степень квадратной матрицы 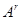 может равняться нулевой, даже если
может равняться нулевой, даже если  – ненулевая матрица. Если
– ненулевая матрица. Если 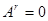 для некоторого положительного числа
для некоторого положительного числа 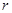 , то
, то  называется нильпотентной матрицей.
называется нильпотентной матрицей.
Подобно многочлену от числовой переменной 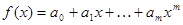 существует понятие многочлена от матрицы:
существует понятие многочлена от матрицы: 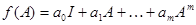 , где коэффициенты
, где коэффициенты 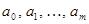 являются вещественными или комплексными числами. Формально многочлен от матрицы можно рассматривать как результат подстановки в алгебраический многочлен
являются вещественными или комплексными числами. Формально многочлен от матрицы можно рассматривать как результат подстановки в алгебраический многочлен 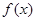 вместо переменной
вместо переменной 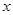 квадратной матрицы
квадратной матрицы  . При этом матричный многочлен
. При этом матричный многочлен 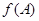 также является квадратной матрицей того же порядка, что и матрица
также является квадратной матрицей того же порядка, что и матрица  . Правила действий над многочленами от матрицы подобны соответствующим правилам для обычных (скалярных) многочленов.
. Правила действий над многочленами от матрицы подобны соответствующим правилам для обычных (скалярных) многочленов.
Над прямоугольными матрицами любых размеров может выполняться операция, называемая кронекеровым произведением. Кронекерово (прямое, тензорное) произведение 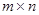 -матрицы
-матрицы  на
на 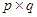 -матрицу
-матрицу 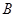 обозначается
обозначается 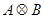 и выражается матрицей размера
и выражается матрицей размера 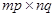 :
:
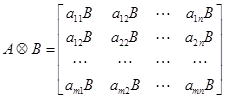 .
.
Можно показать, что при существовании обычных матричных произведений 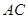 и
и 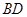 справедливо соотношение:
справедливо соотношение: 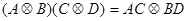 . Имеют место также следующие свойства кронекерового произведения:
. Имеют место также следующие свойства кронекерового произведения: 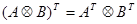 и
и 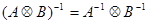 .
.
Преобразование матрицы  , состоящее в замене строк столбцами (или столбцов строками) при сохранении их нумерации, называется транспонированием. Полученная в результате такого преобразования матрица называется транспонированной к матрице
, состоящее в замене строк столбцами (или столбцов строками) при сохранении их нумерации, называется транспонированием. Полученная в результате такого преобразования матрица называется транспонированной к матрице  и обозначается
и обозначается 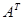 .
.
Произвольная 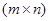 -матрица при транспонировании становится
-матрица при транспонировании становится 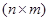 -матрицей, а элемент
-матрицей, а элемент 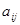 занимает
занимает 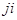 клетку, т. е.
клетку, т. е. 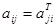 . Если квадратная матрица совпадает со своей транспонированной, т. е.
. Если квадратная матрица совпадает со своей транспонированной, т. е. 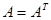 , то она называется симметричной и ее элементы связаны соотношением
, то она называется симметричной и ее элементы связаны соотношением 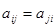 (симметрия относительно главной диагонали). Матрица, для которой
(симметрия относительно главной диагонали). Матрица, для которой 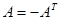 называется кососимметричной, и ее элементы связаны соотношением
называется кососимметричной, и ее элементы связаны соотношением 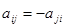 . Она, как и симметричная матрица, всегда квадратная, но диагональные элементы равны нулю, т. е.
. Она, как и симметричная матрица, всегда квадратная, но диагональные элементы равны нулю, т. е. 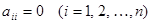 . Ниже приведены примеры симметричной матрицы
. Ниже приведены примеры симметричной матрицы  и кососимметричной матрицы
и кососимметричной матрицы  :
:
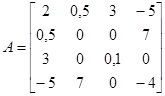 ;
; 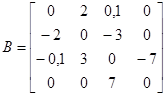 .
.
Ясно, что не все элементы таких матриц могут быть выбраны произвольно. Можно убедиться, что из 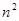 элементов для симметричной матрицы независимыми могут быть только
элементов для симметричной матрицы независимыми могут быть только 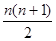 , а для кососимметричной –
, а для кососимметричной – 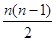 элементов.
элементов.
Комплексно-сопряженная и транспонированная матрица 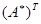 называется сопряженной с
называется сопряженной с  . Матрица, равная своей сопряженной, т. е.
. Матрица, равная своей сопряженной, т. е. 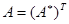 , называется эрмитовой. Если
, называется эрмитовой. Если 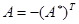 то
то  – косоэрмитова матрица.
– косоэрмитова матрица.
Легко показать, что транспонирование произведения 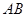 равно произведению транспонированных матриц, взятых в обратном порядке:
равно произведению транспонированных матриц, взятых в обратном порядке: 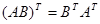 . Дважды транспонированная матрица равна исходной, т. е.
. Дважды транспонированная матрица равна исходной, т. е. 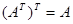 .
.
В обычной алгебре два числа, произведение которых равно единице, называют взаимно обратными. Число, обратное числу 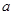 , обозначается через
, обозначается через 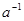 и по определению
и по определению 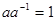 . Аналогично в матричной алгебре две квадратные матрицы, произведение которых равно единичной матрице, т. е.
. Аналогично в матричной алгебре две квадратные матрицы, произведение которых равно единичной матрице, т. е. 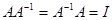 , называют взаимно обратными (матрица
, называют взаимно обратными (матрица 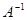 является обратной к матрице
является обратной к матрице  ). Однако на этом аналогия заканчивается. Выражение
). Однако на этом аналогия заканчивается. Выражение 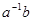 , где
, где 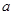 и
и 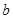 – числа, можно представить как частное от деления
– числа, можно представить как частное от деления 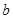 на
на 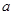 , но для матриц такое представление не имеет смысла и в общем случае
, но для матриц такое представление не имеет смысла и в общем случае 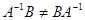 . Поэтому вместо операции деления
. Поэтому вместо операции деления 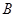 на
на  различают левое частное
различают левое частное 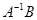 и правое частное
и правое частное 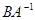 , которые сводятся к умножению слева или справа на обратную матрицу
, которые сводятся к умножению слева или справа на обратную матрицу 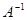 .
.
Часто приходится иметь дело с матрицами, элементами которых являются не числа, а функции от скалярного аргумента (времени 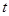 или любой другой переменной). Дифференцирование и интегрирование таких матриц сводится к правилам, аналогичным обычным правилам дифференцирования и интегрирования с одним существенным отличием. Так как произведение матриц в общем случае некоммутативное, то необходимо следить за сохранением первоначального порядка следования сомножителей. Пусть матрица
или любой другой переменной). Дифференцирование и интегрирование таких матриц сводится к правилам, аналогичным обычным правилам дифференцирования и интегрирования с одним существенным отличием. Так как произведение матриц в общем случае некоммутативное, то необходимо следить за сохранением первоначального порядка следования сомножителей. Пусть матрица 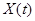 размера
размера 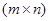 имеет своими элементами дифференцируемые функции
имеет своими элементами дифференцируемые функции 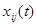 скалярного аргумента
скалярного аргумента 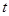 . Производная матрицы
. Производная матрицы 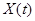 по переменной
по переменной 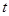 определяется как
определяется как
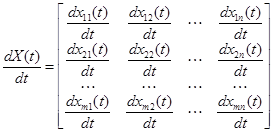 ,
,
т. е. дифференцирование матрицы сводится к дифференцированию всех ее элементов по той же переменной. Имеют место также соотношения:
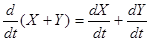 ;
; 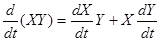 .
.
Если в первом из приведенных соотношений порядок следования матриц и их производных безразличен, то во втором он должен быть строго выдержан.
Интеграл от матрицы 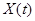 определяется как матрица, элементы которой равны интегралам от соответствующих элементов исходной матрицы, т. е.
определяется как матрица, элементы которой равны интегралам от соответствующих элементов исходной матрицы, т. е.
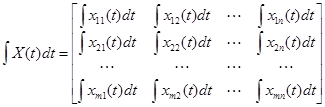 .
.
Контрольные вопросы к лекции 11
11-1. Что называется матрицей?
11-2. Что называется элементом матрицы?
11-3. Когда две матрицы равны?
11-4. Какая матрица называется комплексной?
11-5. Какая матрица называется комплексно сопряженной?
11-6. Какая матрица называется диагональной?
11-7. Какая матрица называется единичной?
11-8. Какая матрица называется треугольной?
11-9. Как находится сумма двух матриц одинакового размера?
11-10. Как находится произведение матрицы на скаляр?
11-11. Как находится разность двух матриц одинаковых размеров?
11-12. Как находится произведение матрицы  размера (
размера ( 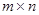 ) на матрицу
) на матрицу 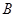 размера (
размера ( 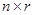 )?
)?
11-13. Когда существует произведение матрицы  на матрицу
на матрицу 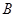 ?
?
11-14. Что получается в результате умножения матрицы на столбец?
11-15. Что получается в результате умножения строки на матрицу?
11-16. Что получается в результате умножения строки на столбец?
11-17. Что получается в результате умножения столбца на строку?
11-18. Какие матрицы называются коммутирующими?
11-19. Что представляет собой степень матрицы?
11-20. Какая матрица называется нильпотентной?
11-21. Что представляет собой многочлен от матрицы?
11-22. Как получается кронекерово произведение матриц?
11-23. Какое преобразование матрицы называется транспонированием?
11-24. Какая квадратная матрица называется симметричной?
11-25. Какая квадратная матрица называется кососимметричной?
11-26. Какая матрица называется эрмитовой?
11-27. Какая матрица называется косоэрмитовой?
11-28. Какая матрица называется обратной?
11-29. Как определяется производная матрицы 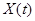 по переменной
по переменной 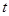 ?
?
11-30. Как определяется интеграл от матрицы 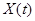 ?
?
Дата добавления: 2016-09-06; просмотров: 2825;











