Алгоритм минимизации конечного автомата

Шаг 1: два состояния s и t относим в один класс 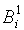, если для любого входного символа x значение функции выхода s совпадает со значениями функции выхода t. В результате получим r классов:

.

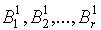M

Шаг k: два состояния s и t из одного класса 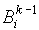, полученного на предыдущем шаге, относим в один класс 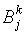, если для любого значения входного символа значения функций состояний принадлежат одному и тому же классу из предыдущего шага. Если шаг k не изменяет разбиения, то процесс останавливается. Доопределяем функции перехода и выхода и строим таблицу переходов –выходов.

Пример. Минимизировать автомат, заданный таблицей:

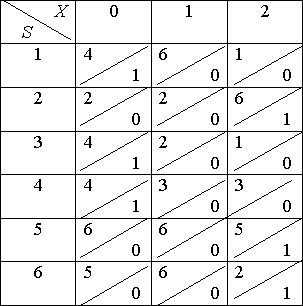
Шаг 1: Первое, третье и четвертое состояния отнесем в один класс состояний, а второе, пятое и шестое – в другой:

;

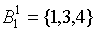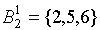
Шаг 2: Выпишем значения функции переходов для состояний из класса :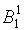

; ;

; ;

; ;

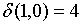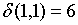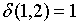
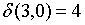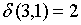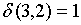
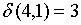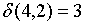
Видно, что 1 и 3-е состояния относим в один класс этого шага 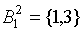, а четвертое состояние – в другой 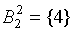. Проанализировав аналогичным образом значения функции выходов для состояний из класса 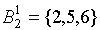, видим:

; ;

; ;

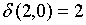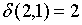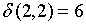
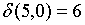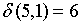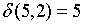
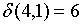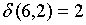; ; , т.е. все они остаются в одном классе. В результате получим разбиение на классы:

; ;

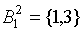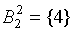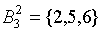
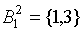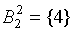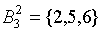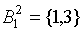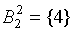Шаг 3: ; ; . Дальнейшего разбиения классов не происходит, поэтому процесс останавливается. Класс назовем состоянием , класс состояний назовем состоянием , а класс 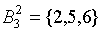– состоянием .

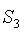Построим таблицу переходов–выходов:

Построенный автомат – минимальный.

Лекция 5.

4.5. Каноническая таблица. Канонические уравнения

Реализация К.Д.А. осуществляется на основе канонических уравнений, которые находятся с помощью канонической таблицы. Каноническая таблица строится следующим образом по таблице переходов–выходов или диаграмме Мура.

Аргументы функций l и d находятся в столбцах слева, а справа – их значения.

S\X		…		…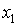
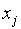
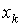
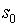
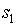
M
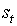
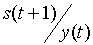
M

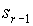
s(t)	x(t)	y(t)	s(t+1)
…	…	…	…
…	…	…	…
…	…	…	…
…	…	…	…

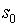
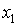
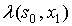
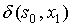
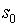
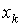
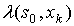
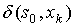
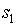
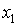
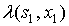
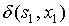
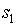
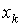
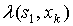
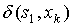
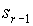
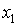
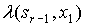
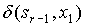
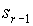
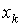
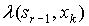
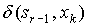
Канонические уравнения имеют вид:

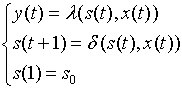
Элементы множеств S, X, Y кодируют двоичными наборами, соблюдая при этом следующие условия:

1. разным элементам в каждом из множеств S, X, Y соответствуют разные кодовые наборы;
2. длины кодовых наборов в каждом из множеств S, X, Y должны совпадать и быть по возможности минимальными;
3. начальному состоянию соответствует набор .

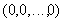После кодирования 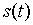, , 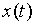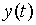принимают вид:

=

=

=

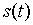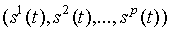
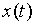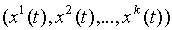
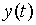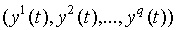
Таблица преобразовывается к скалярному виду следующим образом:

	…		…		…			…
…	.	…		…		…	…		…

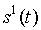
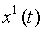
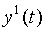
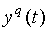
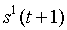
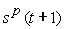
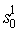
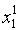
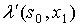
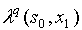
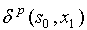
Для того, чтобы представить 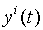, 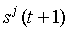как булевы функции, необходимо, чтобы они были всюду определены. С этой целью к таблице добавляются строки, содержащие в левой части недостающие наборы, а в правой части – прочерки. Затем, прочерки заполняются 0 и 1 (функции доопределяются) так, чтобы по соответствующим столбцам значений l и d можно было записать формулу в виде СКНФ или СДНФ или в каком-нибудь другом наиболее простом виде.