Устойчивость пластин при комбинированном нагружении

Комбинированным нагружением, а точнее - комби-напряженным состоянием принято называть такое докритическое состояние, где по крайней мере два из трех усилий 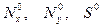отличны от нуля. В задачах устойчивости мы всегда рассматриваем только однопараметрическое нагружение. Иногда комбинированное состояние оказывается однопараметрическим уже по своей природе как, например, в случае нагружения консольной тонкостенной балки силой на конце (рис.16.3).

Если стенка такова, что нормальными напряжениями в ней пренебречь нельзя, то сопроматовское решение дает

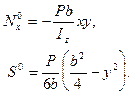
Другой пример - пластина при одноосном сжатии, закрепленная в своей плоскости так, что поперечные перемещения невозможны. Тогда, приняв, что 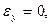получаем .

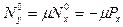В подобных случаях исследование устойчивости ведется традиционно на основе уравнения (13.17) или критерия (15.1) с удержанием имеющихся докритических сил.

Чаще требуется выбрать параметры пластины для нескольких расчетных случаев или при поверочных расчетах - найти несущую способность, т.е. выяснить, какую предельную комбинацию различных нагрузок может выдержать конкретная пластина.

Проиллюстрируем логику исследования на примере пластины, шарнирно опертой по всему контуру.

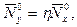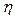I. Пусть где - некоторый параметр.

Тогда для критических напряжений, решая задачу в двойных рядах, получим

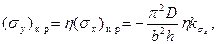
где

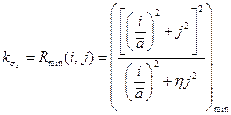. (16.18)

В зависимости от удлинения 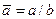при различных фиксированных 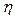значения 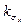представлены на рис.16.5.

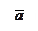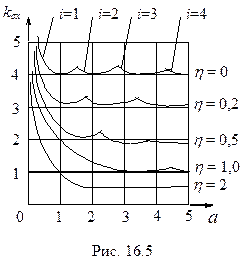
Для пластин с определенным 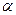, поднимаясь до различных 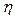, находим 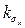и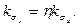

Возможны и другие графические интерпретации зависимости (16.18).

2. Пусть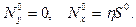

Отыскивая решение в форме (16.4), получим

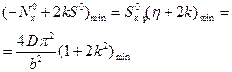. (16.19)

В частности, при 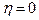(чистый сдвиг) имеем

,

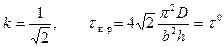при 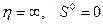получаем

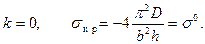
При конечных значениях 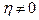(16.19) можно записать в виде

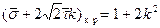. (16.20)

Если задаться значением 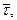то минимизируя (16.20) по 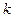, найдем

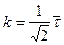. (16.21)

Подставим (16.21) в (16.20), получим

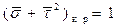. (16.22)

Соотношение (16.22) справедливо при любых значениях 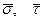и, в частности, при растяжении 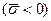. Тогда 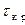будут больше, чем при чистом сдвиге.

Связь 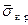с 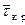можно представить графически (Рис.16.22). Область под кривой - зона устойчивости.

Аналогично исследуются и другие комбинированные напряженные состояния.