Комплексные числа, как векторы на плоскости
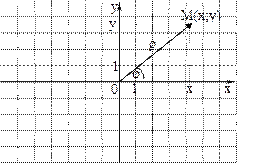
Пусть задано комплексное число 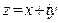 . Отметим на плоскости точку . Отметим на плоскости точку 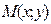 с координатами, которые являются соответственно действительной и мнимой частями заданного комплексного числа. Множество комплексных чисел взаимно однозначно соответствует множеству точек с координатами, которые являются соответственно действительной и мнимой частями заданного комплексного числа. Множество комплексных чисел взаимно однозначно соответствует множеству точек
| 
|
на этой плоскости. Построенную плоскость в этом случае называют комплексной плоскостью. Вспомним, что при сложении комплексных чисел действительная и мнимая части этих чисел складываются, при вычитании комплексных чисел действительная и мнимая части этих чисел вычитаются, при умножении комплексных чисел на действительное число действительная и мнимая части этих чисел умножаются на это число. Но именно так и происходят действия с обычными геометрическими векторами. В этом и заключается геометрический смысл указанных операций над комплексными числами.
Более того, в некоторых книгах вы можете встретить определение комплексных чисел, как пары действительных чисел с соответствующим образом введенными операциями сложения и умножения. Такое определение эквивалентно данному в этой лекции.
Дата добавления: 2016-09-06; просмотров: 1660;











