TWO WAYS TO REPRESENT MEANING

To represent the entities and relationships mentioned in the texts, the following two logically and mathematically equivalent formalisms are used:

· Predicative formulas. Logical predicates are introduced in mathematical logic. In linguistics, they are used in conventional logical notation and can have one or more arguments. Coherence of a text is expressed in the first place by means of common arguments for the predicates involved. For example, the meaning of the sentence Las niñas pequeñas ven la flor roja is represented by the following conjunctive predicative formula:

VER(niña, flor) &

MUCHO(niña) &

PEQUEÑO(niña) &

SOLO(flor) &

ROJO(flor)

In such representation, predicates SOLO and MUCHO have the meanings ‘number of the entities given by the argument is one’ and ‘number of the entities given by the argument is more than one,’ respectively. Arguments of the predicates that are not predicates by themselves are called terms. They are written in lowercase letters, in contrast to the predicates that are written in uppercase.

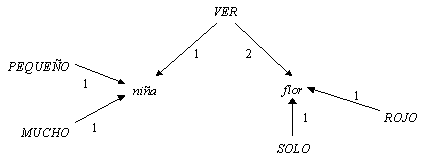FIGURE IV.8. Semantic network for the sentence Las niñas pequeñas ven la flor roja.

· Directed labeled graphs. The nodes of these graphs represent the terms or predicates, and the arrows connect predicates with their arguments, i.e., terms or other predicates. The arrows are marked with numeric labels according to the number of the corresponding argument (1^st argument, 2^nd, etc.). Though each predicate assigns to each its argument a specific semantic role, the numerical labels in the graph are used only to distinguish the arguments. For predicates denoting actions, the label 1 usually marks the agent, the label 2, patient or target, etc. Nevertheless, a label of such type does not make any semantic allusion, the enumeration being rather arbitrary. Thus, the graph representation is just equivalent to the predicate one rather than provides any additional information. The semantic representation in the form of directed labeled graph is often called semantic network. Figure IV.8 shows the semantic network representation for the example above.

These two representations are equivalent, and either of them can be used. Indeed, there exist a number of easy ways to encode any network linearly.

For human readers, in books and articles, the graph representation is especially convenient. For internal structures of a computer program, the equivalent predicative representation is usually preferred, with special formal means to enumerate the referentially common arguments of various logical predicates.

The graph representation explicitly shows the commonality of the arguments, making it obvious what is known about a specific entity. In the drawing shown in the Figure IV.8, for example, it is immediately seen that there are three pieces of information about the terms niña and flor, two pieces about the predicate VER, and one for predicate ROJO and SOLO.

Some scientists identify the representations of Meaning with the representation of human knowledge in general^[15]. The human knowledge is of concern not only for natural language processing, but also for the task of transferring knowledge between computers, whether that knowledge is expressed by natural language or by some other means. For the transfer of knowledge, it is important to standardize methods of representation, so that the knowledge can be communicated accurately. Just for these purposes, the computer community is developing knowledge representation in both the linear and the graphical format. The accuracy and utility of any representation of knowledge should be verified in practice, i.e., in applications.

In the opinion of other scientists, the representations of Meaning and of human knowledge can operate by the same logical structures, but the knowledge in general is in no way coincident with purely linguistic knowledge and even can have different, non-discrete, nature. Hence, they argue, for the transition from Meaning in its linguistic sense to the corresponding representation in terms of general human knowledge, some special stage is needed. This stage is not a part of language and can operate with tools not included in those of the language proper.