Нормальные формы функций алгебры логики
Закон функционирования сложных логических устройств записывается в виде алгебраического выражения (ФАЛ) в канонической форме, к которым относится совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
Совершенная дизъюнктивная нормальная форма ФАЛ. Рассмотрим понятие конституенты единицы. Допустим, что функция двух переменных f(x2, x1) на всех наборах их значений равна 1, т.е. является элементарной функцией тождественно равной 1. Представим эту функцию в виде суммы четырех (по числу номеров наборов) конъюнкций двух таких переменных, каждой из которых в таблице истинности (f15, см. табл. 3) соответствует свой набор значений x2 и x1, на котором конъюнкция этих переменных принимает единичной значение:
f(x2, x1) = 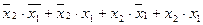 .
.
Каждое логическое произведение двух переменных в данной сумме представляет собой конституенту единицы, которую называют иногда минитермом.
Можно показать, что любую функцию алгебры логики можно представить в виде суммы произведений каждой конституенты единицы на значение функции, которое она принимает на том наборе значений переменных x2 и x1, на котором данная конституента единицы равна 1:
f(x2, x1) = 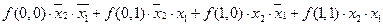
Действительно, если на каком-либо наборе значений переменных x2 и x1 ФАЛ равна нулю, то, естественно, и произведение равно нулю и его можно не писать. Допустим f(1, 1) = 1, а на остальных наборах значений переменных функция равна нулю. Тогда справедлива следующая запись:
f(x2, x1) = 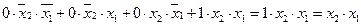 .
.
Оставляя те конституенты единицы, которые принимают единичное значение на тех же наборах значений переменных, что и функция, получим запись ФАЛ в СДНФ.
Следовательно, СДНФ функции алгебры логики представляет собой алгебраическое выражение, которое составлено из дизъюнкции конституент единицы и принимает значение, равное 1 на тех наборах значений переменных, на которых значение заданной функции равно 1. Так, например, для функции ИЛИ (f7, см. табл. 3):
f(x2, x1) = 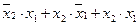 .
.
Для составления алгебраического выражения в СДНФ следует взять дизъюнкцию таких конституент единицы, которые соответствуют наборам значений переменных, на которых функция равна 1:
f(x1, x2, … , xn) = f(j1, j2, … , jm) = Kj1, Kj2, … , Kjm,
где j1, j2, … , jm – номера наборов значений переменных, на которых функция равна 1;
Kj1, Kj2, … , Kjm – конституенты единицы, принимающие единичное значение на этих номерах наборов значений переменных.
Пример. Пусть ФАЛ трех переменных задана числовым способом f1(1, 5, 7), тогда СДНФ этой функции примет следующий вид:
f(x3, x2, x1) = f1(1, 5, 7) = 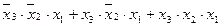 .
.
Здесь первое слагаемое (конституента 1) принимает единичное значение на наборе 001, соответствующем номеру 1, второе – на наборе 101, соответствующем номеру 5, третье – на наборе 111, соответствующем номеру 7.
Используя аксиому х = х + х, представим нашу функцию в следующем виде:
f1(1, 5, 7) = 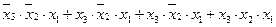 .
.
Используя распределительный закон, вынесем за скобки в данном выражении конъюнкции вида: 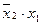 и х3 ∙ х1.
и х3 ∙ х1.
f1(1, 5, 7) = 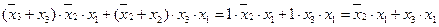 .
.
Мы получили более простое равносильное выражение для нашей функции, имеющее меньшее число вхождений переменных в функцию по сравнению с СДНФ. Такую форму представления ФАЛ в виде дизъюнкции элементарных конъюнкций обычно называют дизъюнктивной нормальной формой (ДНФ). Любая ФАЛ может иметь одну или несколько равносильных ДНФ и только одну СНДФ.
Совершенная конъюнктивная нормальная форма ФАЛ. Наряду с СДНФ для записи ФАЛ в виде алгебраического выражения в равной мере используют совершенную конъюнктивную нормальную форму СКНФ, которая представляет собой алгебраическое выражение, принимающее значение 0 на тех наборах значений переменных, на которых значение заданной функции также равно 0.
Рассмотрим понятие конституенты нуля, называемой иногда макстермом. Допустим, что функция двух переменных f(x2, x1) на всех наборах их значений принимает значение, равное 0, т.е. является элементарной функцией тождественно равной 0. Представим эту функцию в виде логического произведения (конъюнкции) четырех (по числу номеров наборов) дизъюнкций двух таких переменных, каждой из которых в таблице истинности (f0, см. табл. 3) соответствует свой набор значений x2 и x1, на котором дизъюнкция этих переменных принимает нулевое значение:
f(x2, x1) = 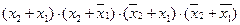 .
.
Каждое логическая сумма двух переменных в данном произведении представляет собой конституенту нуля.
Можно показать, что любую функцию алгебры логики можно представить в виде конъюнкции логических сумм, составленных из конституенты нуля и значения функции, которое она принимает на том наборе значений переменных x2 и x1, на котором данная конституента нуля равна 0:
f(x2, x1) = 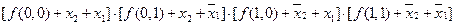
Действительно, если на каком-либо наборе значений переменных x2 и x1 ФАЛ равна единице, то, естественно, и сумма равно 1 и ее можно не писать. Допустим f(1, 1) = 0, а на остальных наборах значений переменных функция равна единице. Тогда справедлива следующая запись:
f(x2, x1) = 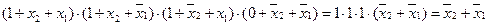 .
.
Оставляя те конституенты нуля, которые принимают нулевое значение на тех же наборах значений переменных, что и функция, получим запись ФАЛ в СКНФ.
Следовательно, СКНФ функции алгебры логики представляет собой алгебраическое выражение, которое составлено из конъюнкции конституент нуля и принимает значение, равное 0, на тех наборах значений переменных, на которых значение заданной функции равно 0. Так, например, для функции ИЛИ (f7, см. табл. 3):
f(x2, x1) = 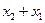 .
.
Для составления алгебраического выражения в СКНФ следует взять конъюнкцию таких конституент нуля, которые соответствуют наборам значений переменных, на которых функция равна 0:
f(x1, x2, … , xn) = f(i1, i2, … , im) = Mi1, Mi2, … , Mik,
где i1, i2, … , im – номера наборов значений переменных, на которых функция равна 0;
Mi1, Mi2, … , Mik – конституенты нуля, принимающие нулевое значение на этих номерах наборов значений переменных.
Пример. Пусть ФАЛ трех переменных задана числовым способом f1(1, 5, 7), следовательно, нулевые значения функции принимает на наборах c номерами (0, 2, 3, 4, 6), тогда СКНФ этой функции примет следующий вид:
f0(0, 2, 3, 4, 6) = 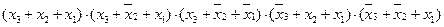 .
.
Здесь первый множитель (конституента 0) принимает нулевое значение на наборе 000, соответствующем номеру 0; второй – на наборе 010, соответствующем номеру 2; третий – на наборе 011, соответствующем номеру 3; четвертый – на наборе 100, соответствующем номеру 4; пятый – на наборе 110, соответствующем номеру 6.
Наряду с СКНФ любая ФАЛ может быть представлена в более простой конъюнктивной нормальной форме (КНФ), которая является конъюнкцией элементарных дизъюнкций.
Например, нашу функцию после проведения минимизации ее аналитического выражения в СКНФ можно представить в виде следующей КНФ:
f0(0, 2, 3, 4, 6) = 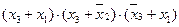 .
.
Проведя соответствующие логические преобразования функции с использованием основных законов алгебры логики и аксиом, мы можем перейти от КНФ нашей функции к ее ДНФ. Выполним двойную инверсию исходной функции:

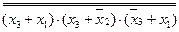 .
.
Используя правило де Моргана, произведем инверсию выражения под знаком двойной инверсии:
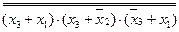 =
= 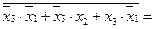
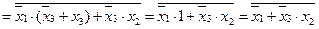 .
.
Используя распределительный закон, преобразуем выражение под знаком инверсии, а затем инвертируем преобразованное выражение по правилу де Моргана:
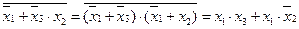 .
.
Полученное алгебраическое выражение для заданной ФАЛ полностью совпадает с той ДНФ, которую мы получили ранее для этой же функции при рассмотрении СДНФ. Таким образом, для одной и той же функции мы можем иметь два равносильных аналитических выражения для заданной функции: одно в КНФ, другое в ДНФ.
Переход от канонической формы записи ФАЛ к более простой типа ДНФ или КНФ возможен посредством использования различных методов минимизации алгебраических выражений ФАЛ.
Задачи для самостоятельного решения
1. Для функции трех переменных у = f(x3, x2, x1), заданной таблицей истинности, составить алгебраическое выражение в СДНФ.
| № набора | ||||||||
| х3 | ||||||||
| х2 | ||||||||
| х1 | ||||||||
| у |
Ответ: 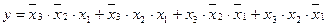 .
.
2. Для функции трех переменных у = f(x3, x2, x1), заданной таблицей истинности из задачи 1, составить алгебраическое выражение в СКНФ.
Ответ: 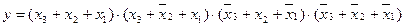 .
.
3. Для функции трех переменных у = f(x3, x2, x1) = f1(2, 3, 5, 7), заданной числовым способом, составить алгебраическое выражение в СДНФ.
Ответ: 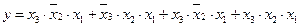 .
.
4. Для функции трех переменных у = f(x3, x2, x1) = f0(2, 3, 5, 7), заданной числовым способом, составить алгебраическое выражение в СКНФ.
Ответ: 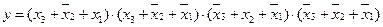 .
.
5. Для функции трех переменных у = f(x3, x2, x1) = f0(2, 3, 5, 7), заданной числовым способом, составить алгебраическое выражение в СДНФ.
Ответ: 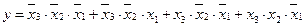 .
.
6. Для функции трех переменных у = f(x3, x2, x1) = f1(2, 3, 5, 7), заданной числовым способом, составить алгебраическое выражение в СКНФ.
Ответ: 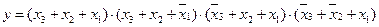 .
.
7. Для функции трех переменных у = f(x3, x2, x1), заданной картой Карно, составить алгебраическое выражение в СДНФ.
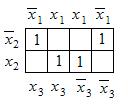
Ответ: 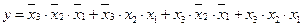 .
.
8. Для функции трех переменных у = f(x3, x2, x1), заданной картой Карно из задачи 7, составить алгебраическое выражение в СКНФ.
Ответ: 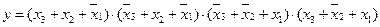 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Состав и виды издержек предприятия | | | Своеобразие в проявлении свойств и типов восприятия при нарушениях зрения. |
Дата добавления: 2016-09-06; просмотров: 3424;











