Словесная запись алгоритмов

Самой распространенной формой представления алгоритмов, адресуемых человеку, является обычная словеснаязапись. В этой форме могут быть выражены любые алгоритмы. Но если такой алгоритм предназначен для его дальнейшей реализации на вычислительном устройстве, то принято придерживаться более формализованного способа построения фраз с тщательно отобранным набором слов. Кроме того, необходимо указывать начало и конец алгоритма, отмечать момент ввода в вычислительное устройство значений исходных данных и вывода/печати полученного результата. В вычислительных алгоритмах широко используется общепринятая математическая символика, язык формул. Вводится необходимая в вычислительной практике операция присваивания:

у := А

(читается: «у присвоить значение А»), где у – переменная; А – некоторое выражение/формула. Следует сначала выполнить все действия, предусмотренные формулой А, а затем полученный результат сохранить в качестве значения переменной у. Выражение А в частном случае может быть переменной или числом.

Предположим, что правила выполнения арифметических операций сложения, вычитания и умножения известны исполнителю. Тогда искомым алгоритмом будет следующая система предписаний:

Начало.

1. Ввести x₁, x₂.

2. p = –(x₁+x₂).

3. q = x₁x₂.

4. Вывести p, q.

Конец.

Схемы алгоритмов

Схема алгоритма – это графический способ его представления с элементами словесной записи. Каждое предписание алгоритма изображается с помощью плоской геометрической фигуры – блока. Отсюда название: блок-схема. Переходы от предписания к предписанию изображаются линиями связи – линиями потоков информации, а направление переходов – стрелками. Различным по типу выполняемых действий блокам соответствуют различные геометрические фигуры. Приняты определенные стандарты (ГОСТ 19.701-90) графических изображений блоков (таблица).

Рассмотрим общие правила построения схем алгоритмов.

1. Для конкретизации содержания блока и уточнения выполняемого действия внутри блока помещаются краткие пояснения – словесные записи с элементами общепринятой математической символики.

Наименование символа	Обозначение и размеры	Функция
Процесс (вычислительный блок)		Выполнение операции или группы операций, в результате которых изменяются значение, форма представления или расположение данных
Решение (логический блок)		Выбор направления выполнения алгоритма в зависимости от некоторых условий
Модификация (заголовок цикла)		Выполнение операций по управлению циклом – повторением команды или группы команд алгоритма
Пуск-останов (начало-конец)		Начало или конец выполнения программы или подпрограммы
Предопределенный процесс (вызов подпрограммы)		Вызов и использование ранее созданных и отдельно описанных алгоритмов (подпрограмм)
Ввод/вывод		Общее обозначение ввода или вывода данных в алгоритме безотносительно к внешнему устройству
Соединитель		Указание прерванной связи между блокам в пределах одной страницы
Межстраничный соединитель		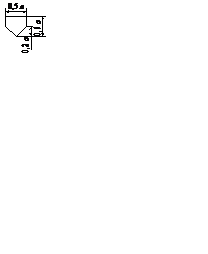Указание прерванной связи между блоками, расположенными на разных листах

2. Основное направление потока информации в схемах может не отмечаться стрелками. Основное направление – сверху вниз и слева направо. Если очередность выполнения блоков не соответствует этому направлению, то возможно применение стрелок.

3. По отношению к блоку линии могут быть входящими и выходящими. Количество входящих линий принципиально не ограничено. Количество выходящих линий регламентировано и зависит от типа блока. Например, логический блок должен иметь не менее двух выходящих линий, каждая из которых соответствует одному из возможных направлений вычислений. Блок модификации должен иметь две выходящие линии, одна соответствует повторению цикла, вторая – его окончанию.

4. Допускается разрывать линии потока информации, размещая на обоих концах разрыва специальный символ «соединитель». В пределах одной страницы используется символ обычного соединителя, во внутреннем поле которого помещается маркировка разрыва либо отдельной буквой, либо буквенно-цифровой координатой блока, к которому подходит линия потока. Если схема располагается на нескольких листах, переход линий потока с одного листа на другой обозначается с помощью символа «межстраничный соединитель». При этом на листе с блоком-источником соединитель содержит номер листа и координаты блока-приемника, а на листе с блоком-приемником – номер листа и координаты блока-источника.

5. Нумерация блоков осуществляется либо в левом верхнем углу блока в разрыве его контура, либо рядом слева от блока. Принцип нумерации может быть различным, наиболее простой – сквозная нумерация. Блоки начала и конца не нумеруются.

6. Для блоков приняты следующие размеры: а = 10, 15, 20 мм; b = 1,5а. Если необходимо увеличить размер блока, то допускается увеличение на число, кратное пяти. Необходимо выдерживать минимальное расстояние 3 мм между параллельными линиями потоков и 5 мм между остальными символами.

С помощью блок-схем можно изображать самые различные алгоритмы, например, линейной, разветвляющейся и циклической структур.

Блок-схемы являются исключительно простым и наглядным способом представления алгоритмов. Их очень полезно использовать при разработке общей структуры алгоритма, чтобы отчетливо представить себе алгоритм в целом и проследить все логические связи между его отдельными частями, проверить все ли возможные варианты решения поставленной задачи нашли в нем отражение.

Блок-схемы не накладывают никаких ограничений на степень детализации в изображении алгоритма. Степень детализации определяется программистом. Однако следует помнить, что схемы общего характера мало информативны, а излишне подробные схемы проигрывают в наглядности. При разработке сложных алгоритмов, чтобы понять сущность выполняемых действий и выявить основные связи, алгоритм записывается в виде общей схемы, состоящей из крупных блоков. Блоки соответствуют основным шагам алгоритма (вводу данных, обработке, выводу данных). Затем крупные блоки разбивают на более мелкие, составляя более детальные схемы, позволяющие проверить их логическую правильность.