ПОТЕРИ НАПРЯЖЕНИЯ В ЭЛЕКТРИЧЕСКИХ СЕТЯХ

Параметры и схемы замещения электрических сетей

Номинальным напряжением U_H приемников электроэнергии (электродвигателей, ламп, трансформаторов) называют то напряжение, при котором они нормально работают.

Каждая электрическая сеть характеризуется номинальным напряжением приемников электроэнергии (в том числе и трансформаторов), которые от нее пита­ются.

Напряжение у потребителя (подстанция завода, трансформаторный пункт цеха) или у отдельного приемника (электродвигатель, лампа накаливания) U_n никогда не остается постоянным в течение суток. В процессе нормальной эксплуатации электрической сети наблюдаются плавные закономерные отклонения напряжения от среднего уровня или резкие кратковременные колебания напряжения, вызванные внезапным изменением режимов работы приемников.

Все линии электрической сети обладают активным сопротивлением R_л, реактивным сопротивлением Х_л, активной проводимостью G_л и емкостной проводимостью В_л. Реактивные сопротивления и проводимости линий обусловлены магнитными и электрическими полями, возникающими вокруг проводников с током I_л и напряжением U на всем протяжении линии. Поэтому все параметры линии распределены по всей ее длине l. Но в практических расчетах промышленных электросетей равномерно распределенные параметры линий для простоты заменяют сосредоточенными параметрами. Сосредоточенные параметры схемы замещения ли­нии электропередачи можно определить по формулам

G = ql;

В=b*l;

R_л=г_0*l;

Х_л = Х0*l,

где q —удельная активная проводимость линии, определяемая в основном потерями на коронирование ∆Р_К на 1 км линии, См/км, q = ∆P_k/U²; b — удельная емкостная проводимость линии, зависящая от емкости линии между проводами разных фаз и на землю, См/км; r_о — удельное активное сопротивление линии, известное для проводов и кабелей каждой марки, Ом/км; х_o — удельное индуктивное сопротивление линий, Ом/км, которое почти не зависит от сечения проводов, х₀ = 0,35 ...0,4 Ом/км для воздушных линий всех напряжений до 220 кВ, х₀- 0,08 Ом/км для кабельных линий.

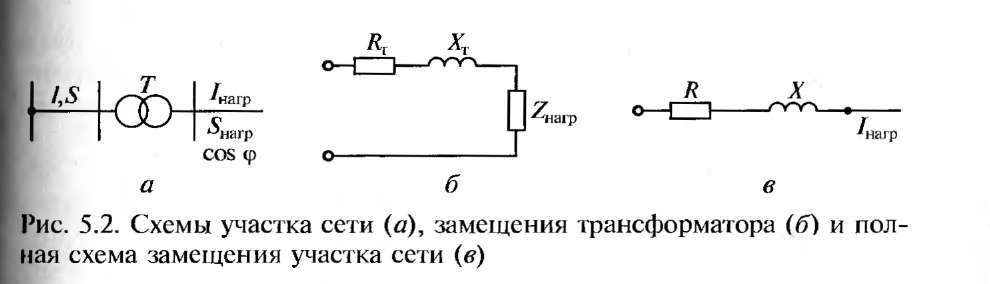
Для линий напряжением 110 кВ и более низкого напряжения проводимости G и В незначительны. Поэтому П-образная схема замещения (см. рис. 5.1, а) заменяется более простой схемой (рис. 5.1, б), содержащей лишь сопротивления R_л и Х_л.

Рассмотрим участок сети, содержащий трансформатор Т (рис. 5.2, а). Схема замещения трансформатора (рис. 5.2, б) представляет собой Г-образную схему, в которой не учтена цепь намагничивания. Индуктивное и активное сопротивления трансформатора Х_т и R_T, Ом, определяются по следующим формулам:

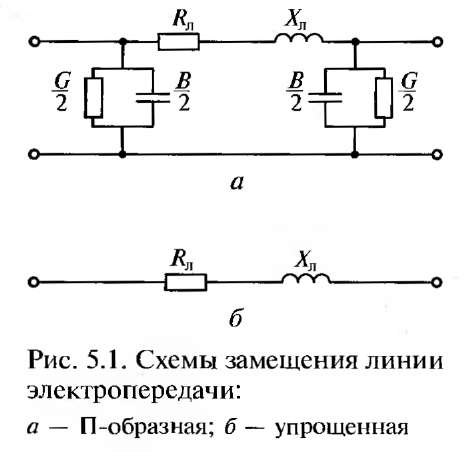R_T=10³*∆P_м*U²_н/S²_т.н

X_т=10*U_к*U²_н/S_т.н

где ∆Рм — потери в меди трансформатора при его номинальной мощности, кВт; U_H — номинальное напряжение сети, для которой проводится расчет, кВ; S_тн — номинальная мощность трансформатора, кВ-А; U_K — напряжение короткого замыкания, %.

Полную схему замещения участка сети можно представить в виде последовательно включенных сопротивлений (рис. 5.2, в) активного

R = R_л + R_т

и индуктивного

Х=Х_л+Х_Т

которое составляют полное сопротивление

z =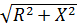

Нагрузку в конце линии на схеме замещения трансформатора (см. рис. 5.2, б) изображают в виде полного сопротивления нагрузки Z_нarp, а на полной схеме замещения (см. рис. 5.2, в) — в виде тока I_нагр или полной мощности S_нагр с указанием коэффициента мощности cosφ.

Определение напряжений в разветвленной электросети. Используя схему замещения, определяют потерю напряжения в линии электропередачи, по которой передается ток нагрузки I. Этот расчет также можно выполнить и для всей цепи (см. рис. 5.2, в) с параметрами R и X.Ha рис. 5.3, а представлена векторная диаграмма токов и напряжений линии, где U_1ф и U_2ф, — векторы фазного напряжения соответственно в начале и конце линии; IR, IX — падения напряжения на активном и реактивном сопротивлениях соответственно.

Арифметическую разность напряжений, измеренных в начале и конце линии, называют потерей напряжения

∆U_ф=U_1ф-U_2ф

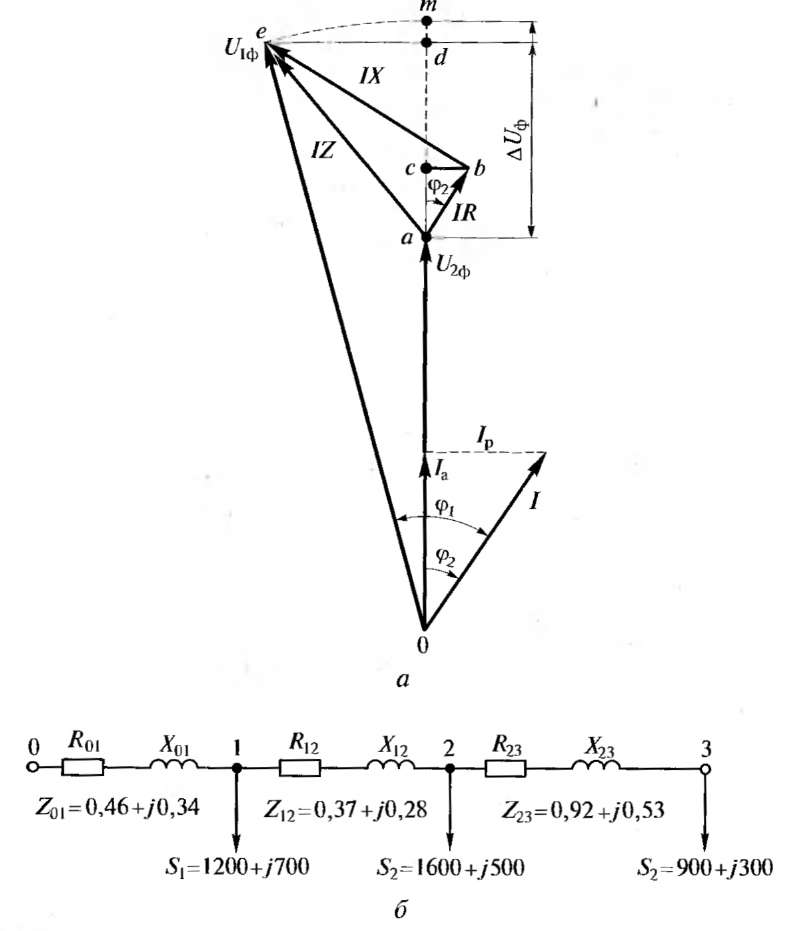
Рис. 5.3. Векторная диаграмма токов и напряжений линии (а) и схема замещения магистральной линии (б)

В рассматриваемом случае (см. рис. 5.3, а) потеря напряжения равна отрезку am. В приближенных расчетах можно считать, что отрезок am равен проекции вектора падения напряжения IZ на направление вектора U_2ф, т.е. отрезку ad.

Исходя из этого допущения

∆U_ф= IR cosφ₂ + IX sinφ₂,

где IR cosф₂ — отрезок ас на векторной диаграмме; IX sin ф₂ — отрезок cd.

Переходя от фазных напряжений к линейным, получают

∆U=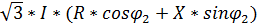

Иногда удобнее вести расчет ∆U в зависимости от передаваемых мощностей Р и Q. Умножив и разделив правую часть выражения (5.12) на номинальное напряжение, приводят это выражение к виду

∆U= (PR + QX)/U

Тогда напряжение в начале линии

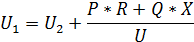
а в конце линии

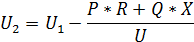
Рассмотренный расчет потерь напряжений и уровней напряжения применяют при радиальной схеме питания нагрузки, подключенной в конце линии, характеризуемой сопротивлениями R и X.