Обтекание цилиндра стационарным потоком с циркуляцией

Предположение об аксиальной симметрии обтекающего потока в ряде случаев не выполняется. Это может являться следствием как асимметрии обтекаемых тел, так и изменения граничных условий. Рассмотрим простейшую модель – обтекание непроницаемого цилиндра радиуса a, расположенного перпендикулярно потоку идеальной несжимаемой жидкости. Будем считать, что всюду в области, занятой жидкостью, движение потенциально, т. е. распределение скоростей описывается потенциалом скорости 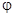, удовлетворяющим уравнению Лапласа в цилиндрических координатах :

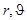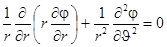
с условием непроницаемости

.

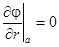Будем как и ранее считать, что возмущение потока жидкости, вносимое цилиндром, убывает на бесконечности, что дает асимптотическое поведение потенциала скорости

.

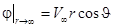Регулярное решение уравнения Лапласа, удовлетворяющее сделанным предположениям, может быть получено методом разделения переменных и имеет вид:

.

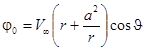Учесть асимметрию обтекания можно путем добавления к потенциалу симметричного распределения скоростей 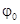потенциала циркуляции :

.

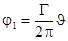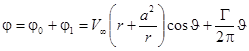Это приводит к асимметричному относительно горизонтальной диаметральной плоскости цилиндра распределению скоростей потока:

.

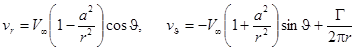Такое поле скоростей является всюду безвихревым, кроме точки 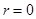. Однако циркуляция вектора скорости по контуру 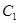, охватывающему цилиндр, отлична от нуля:

.

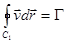Вычисляя с помощью интеграла Бернулли поле давлений, получаем

.

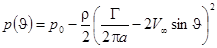Отсюда определяется сила, действующая на единицу длины цилиндра, находящегося в потоке с циркуляцией, которая имеет следующие компоненты:

,

.

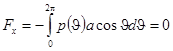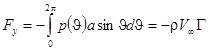Таким образом, поток идеальной несжимаемой жидкости действует на цилиндр с силой, перпендикулярной направлению скорости невозмущенного потока. Эта сила называется подъемной силой Жуковского.