Обтекание шара стационарным потоком

Пусть поток жидкости движется с постоянной скоростью вдоль оси OZ. Потенциал поля скоростей невозмущенного потока (в отсутствие шара) определим выражением:

.

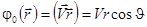Если в жидкости находится шар радиуса а, центр которого совпадает с началом координат, то он возмущает поток жидкости. Будем считать возмущенный поток установившимся и безвихревым. В этом случае потенциал поля скоростей может быть представлен в виде суммы:

,

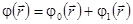где 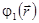- потенциал возмущения, создаваемого шаром. Потенциал возмущения скорости удовлетворяет уравнению Лапласа

.

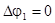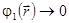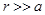Предположим, что возмущение потенциала скорости шаром пренебрежимо мало на больших расстояниях, так что при . Поверхность шара будем считать непроницаемой для жидкости, так что радиальная компонента скорости на поверхности шара обращается в нуль. Это приводит ко второму граничному условию

.

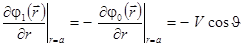Предполагая, что возмущенное течение жидкости также как и движение невозмущенного потока является аксиально-симметричным, для потенциала возмущения получим уравнение (в сферических координатах)

.

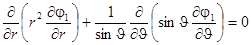Решение уравнения методом разделения переменных

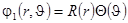
приводит к следующему уравнению для угловой части:

,

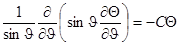где С - константа разделения переменных.

Решение будет регулярным при 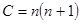и удовлетворять граничному условию на поверхности шара при :

.

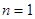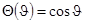Соответственно, радиальное уравнение для возмущения имеет вид

,

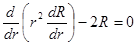и его решение может быть получено подстановкой 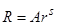. Решение уравнения, удовлетворяющее условию убывания возмущения на бесконечности, существует при 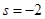. Таким образом, возмущение потенциала, создаваемое непроницаемым шаром заданного радиуса имеет вид:

,

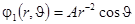а константа А определяется из условия на поверхности шара

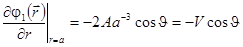
и равна 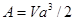. Отсюда окончательно получаем выражения для потенциала возмущения жидкости

,

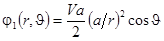а также поле возмущения вектора скорости (в сферических координатах)

.

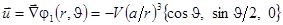Это позволяет определить распределение давления на поверхности шара

,

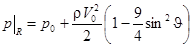где 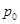– давление в невозмущенном потоке.

Так как распределение давления симметрично относительно экваториальной плоскости 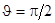, то суммарное силовое воздействие потока идеальной несжимаемой жидкости вдоль направления движения оказывается равным нулю. То есть, воздействие движущейся жидкости на неподвижный шар (или воздействие жидкости на шар, движущейся в ней) равно нулю. Этот результат формально можно получить, вычисляя воздействие потока на элементарную площадку 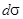на поверхности сферы. В силу аксиальной симметрии потока жидкости сила, действующая на сферу, может быть направлена только вдоль оси :

.

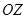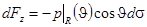Выполняя интегрирование по всей поверхности сферы, получим

.

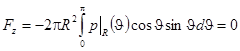Этот эффект называется парадоксом Даламбера.

В системе отсчета, где жидкость покоится, шар движется с постоянной скоростью. Интерпретация парадокса Даламбера в этой системе сводится к утверждению, что идеальная несжимаемая жидкость (при потенциальном обтекании) не оказывает сопротивления движущемуся шару.