Теорема. Достаточный признак монотонности.

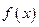1) Если производная функции всюду в интервале положительна, то функция 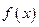в этом интервале возрастает.

2) Если производная 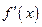от функции 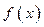всюду в интервале отрицательна, то функция 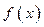в этом интервале убывает.

3) Если производная 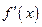от функции 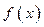всюду в интервале равна нулю, то функция 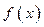в этом интервале не изменяется (константа).

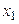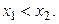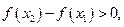Доказательство. Докажем первое утверждение. Возьмем в рассматриваемом интервале две произвольные точки и , причем пусть По формуле Лагранжа Если то так как и то и т .е. 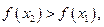ч.т.д.

Аналогично доказываются остальные два случая.

Экстремум функции

Определение 4.7. Точка х₀ называется точкой максимума функции 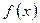, если в некоторой окрестности точки х₀ выполняется неравенство .

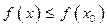Определение 4.8. Точка х₀ называется точкой минимума функции 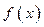, если в некоторой окрестности точки х₀ выполняется неравенство 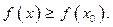(Рис. 4.11, Рис. 4.12).

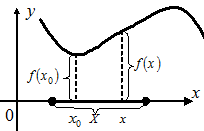
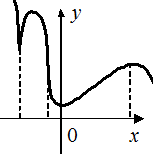
Рис. 4.11 Рис. 4.12 Рис. 4.13

Определение 4.9. Максимум или минимум функции называется экстремумомфункции. Точка максимума или минимума функции называется точкой ее экстремума.

Теорема. Необходимое условие экстремума. Если функция 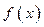в точке 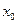, имеет экстремум, то производная обращается в нуль или не существует.

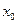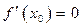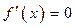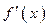Точка , в которой называется стационарной точкой. Точки, в которых или не существует называются критическимиточкамиI рода. Не всякая критическая точка является точкой экстремума.