Теоремы Ролля, Лагранжа и формула Тейлора
Теорема Ролля.Если функция 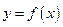 непрерывна на отрезке [a,b], дифференцируема в интервале (а,b) и
непрерывна на отрезке [a,b], дифференцируема в интервале (а,b) и 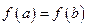 , то в интервале (а,b) найдется хотя бы одно значение
, то в интервале (а,b) найдется хотя бы одно значение 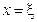 , при котором
, при котором 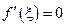 (Рис. 4.7).
(Рис. 4.7).
Если, в частности, 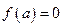 ,
, 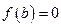 , то теорема Ролля означает, что между двумя корнями функции содержится хотя бы один корень ее производной.
, то теорема Ролля означает, что между двумя корнями функции содержится хотя бы один корень ее производной.
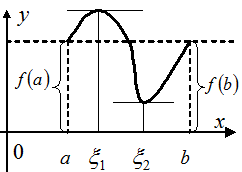
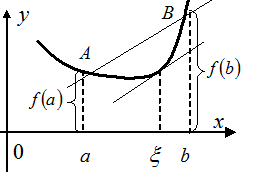
Рис. 4.7 Рис. 4.8
Теорема Лагранжа (о конечном приращении).Если функция 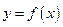 непрерывна на отрезке [a,b] и дифференцируема в интервале (а,b), то в этом интервале найдется хотя бы одно значение
непрерывна на отрезке [a,b] и дифференцируема в интервале (а,b), то в этом интервале найдется хотя бы одно значение 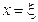 , при котором выполняется равенство
, при котором выполняется равенство 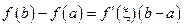 .
.
Доказательство.Рассмотрим функцию 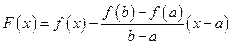 . Эта функция непрерывна на отрезке [a,b] и дифференцируема в интервале (а,b), так как этим условиям удовлетворяет функция
. Эта функция непрерывна на отрезке [a,b] и дифференцируема в интервале (а,b), так как этим условиям удовлетворяет функция 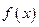 . Очевидно, что и
. Очевидно, что и 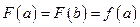 . Поэтому функция
. Поэтому функция 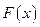 удовлетворяет условиям теоремы Ролля. Следовательно, существует
удовлетворяет условиям теоремы Ролля. Следовательно, существует 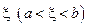 такое, что
такое, что 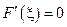 , то есть
, то есть 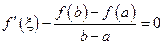 . Отсюда получаем
. Отсюда получаем 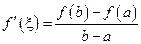 , что и требовалось доказать.
, что и требовалось доказать.
Эти теоремы имеют такой геометрический смысл: на дуге АВ непрерывной кривой 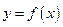 , имеющей в каждой внутренней точке определенную касательную (не параллельную оси Оу), найдется хотя бы одна внутренняя точка, в которой касательная параллельна хорде АВ. (Для теоремы Ролля и хорда АВ, и касательная параллельны оси Ох.) (Рис. 4.7).
, имеющей в каждой внутренней точке определенную касательную (не параллельную оси Оу), найдется хотя бы одна внутренняя точка, в которой касательная параллельна хорде АВ. (Для теоремы Ролля и хорда АВ, и касательная параллельны оси Ох.) (Рис. 4.7).
Формула Тейлора. Функция 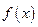 , дифференцируемая
, дифференцируемая 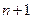 раз в некотором интервале, содержащем точку а, может быть представлена в этом интервале в виде суммы многочлена n-й степени и остаточного члена
раз в некотором интервале, содержащем точку а, может быть представлена в этом интервале в виде суммы многочлена n-й степени и остаточного члена 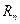 :
:
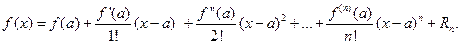
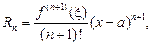 где
где 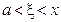 или
или 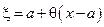 , причем
, причем 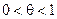 .
.
Дата добавления: 2020-11-18; просмотров: 208;










