Конус. Усеченный конус
Конической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной кривой и точку вне кривой (рис.32).
Данная кривая называется направляющей, прямые – образующими, точка – вершиной конической поверхности.
Прямой круговой конической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной окружности и точку на прямой, которая перпендикулярна плоскости окружности и проходит через ее центр. В дальнейшем эту поверхность будем кратко называть конической поверхностью (рис.33).
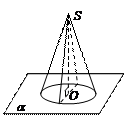
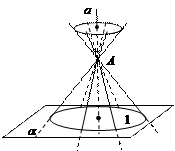 Конусом (прямым круговым конусом) называется геометрическое тело, ограниченное конической поверхностью и плоскостью, которая параллельна плоскости направляющей окружности (рис.34).
Конусом (прямым круговым конусом) называется геометрическое тело, ограниченное конической поверхностью и плоскостью, которая параллельна плоскости направляющей окружности (рис.34).
 | |||
 | |||
Рис. 32 Рис. 33 Рис. 34
Конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг оси, содержащей один из катетов треугольника.
Круг, ограничивающий конус, называется его основанием. Вершина конической поверхности называется вершиной конуса. Отрезок, соединяющий вершину конуса с центром его основания, называется высотой конуса. Отрезки, образующие коническую поверхность, называются образующими конуса. Осью конуса называется прямая, проходящая через вершину конуса и центр его основания. Осевым сечением называется сечение, проходящее через ось конуса. Разверткой боковой поверхности конуса называется сектор, радиус которого равен длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса.
Для конуса верны формулы:
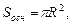
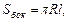 (7)
(7)
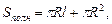
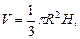
где R – радиус основания;
H – высота;
l – длина образующей;
Sосн – площадь основания;
Sбок – площадь боковой поверхности;
Sполн – площадь полной поверхности;
V – объем конуса.
Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию конуса (рис.35).
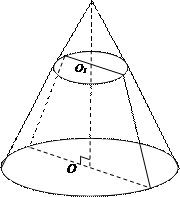 |
Рис. 35
Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной трапеции вокруг оси, содержащей боковую сторону трапеции, перпендикулярную основаниям.
Два круга, ограничивающие конус, называются его основаниями. Высотой усеченного конуса называется расстояние между его основаниями. Отрезки, образующие коническую поверхность усеченного конуса называются образующими. Прямая, проходящая через центры оснований, называется осью усеченного конуса. Осевым сечением называется сечение, проходящее через ось усеченного конуса.
Для усеченного конуса верны формулы:
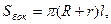 (8)
(8)
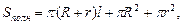
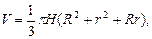
где R – радиус нижнего основания;
r – радиус верхнего основания;
H – высота, l – длина образующей;
Sбок – площадь боковой поверхности;
Sполн – площадь полной поверхности;
V – объем усеченного конуса.
Пример 1.Сечение конуса параллельное основанию делит высоту в отношении 1:3, считая от вершины. Найти площадь боковой поверхности усеченного конуса, если радиус основания и высота конуса равны 9 см и 12 см.
Решение. Сделаем рисунок (рис. 36).
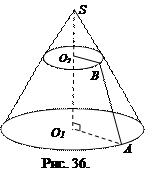
Для вычисления площади боковой поверхности усеченного конуса используем формулу (8). Найдем радиусы оснований О1А и О1В и образующую АВ.
Рассмотрим подобные треугольники SO2B и SO1A, коэффициент подобия 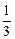 , тогда
, тогда 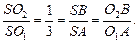
Отсюда 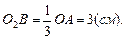
Из 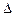 SO1A
SO1A 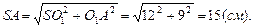
Так как 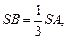 то
то 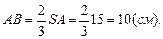
Площадь боковой поверхности усеченного конуса равна:
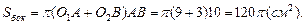
Ответ: 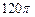
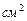 .
.
Пример2. Четверть круга радиуса 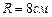 свернута в коническую поверхность. Найти радиус основания и высоту конуса.
свернута в коническую поверхность. Найти радиус основания и высоту конуса.
Решение.Четверить круга является разверткой боковой поверхности конуса. Обозначим r – радиус его основания, H – высота. Площадь боковой поверхности вычислим по формуле: 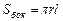 . Она равна площади четверти круга:
. Она равна площади четверти круга: 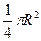 . Получим уравнение
. Получим уравнение 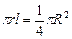 с двумя неизвестными r и l (образующая конуса). В данном случае образующая равна радиусу четверти круга R, значит, получим следующее уравнение:
с двумя неизвестными r и l (образующая конуса). В данном случае образующая равна радиусу четверти круга R, значит, получим следующее уравнение: 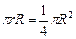 , откуда
, откуда 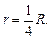 Зная радиус основания и образующую, найдем высоту конуса:
Зная радиус основания и образующую, найдем высоту конуса:
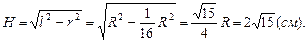
Ответ: 2 см, 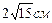 .
.
Пример 3. Прямоугольная трапеция с острым углом 45О, меньшим основанием 3см и наклонной боковой стороной равной 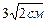 , вращается вокруг боковой стороны перпендикулярной основаниям. Найти объем полученного тела вращения.
, вращается вокруг боковой стороны перпендикулярной основаниям. Найти объем полученного тела вращения.
Решение.Сделаем рисунок (рис. 37).
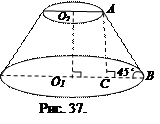
В результате вращения получим усеченный конус, чтобы найти его объем вычислим радиус большего основания и высоту. В трапеции O1O2AB проведем AC^O1B. В 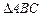 имеем:
имеем: 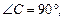
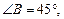
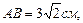 значит, этот треугольник равнобедренный AC=BC=3 см.
значит, этот треугольник равнобедренный AC=BC=3 см.
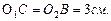
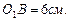
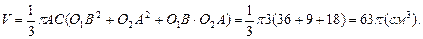 Ответ:
Ответ: 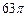
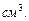
Пример 4.Треугольник со сторонами 13 см, 37 см и 40 см вращается вокруг внешней оси, которая параллельна большей стороне и находится от нее на расстоянии 3 см (Ось расположена в плоскости треугольника). Найти площадь поверхности полученного тела вращения.
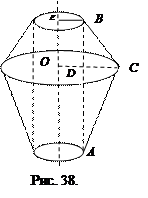 Решение. Сделаем рисунок (рис. 38).
Решение. Сделаем рисунок (рис. 38).
Поверхность полученного тела вращения состоит из боковых поверхностей двух усеченных конусов и боковой поверхности цилиндра. Для того чтобы вычислить эти площади необходимо знать радиусы оснований конусов и цилиндра (BE и OC), образующие конусов (BC и AC) и высоту цилиндра (AB). Неизвестной является только CO. 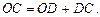
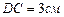 это расстояние от стороны треугольника до оси вращения. Найдем DC. Площадь треугольника ABC с одной стороны равна произведению половины стороны AB на высоту , проведенную к ней DC, с другой стороны, зная все стороны треугольника, его площадь вычислим по формуле Герона:
это расстояние от стороны треугольника до оси вращения. Найдем DC. Площадь треугольника ABC с одной стороны равна произведению половины стороны AB на высоту , проведенную к ней DC, с другой стороны, зная все стороны треугольника, его площадь вычислим по формуле Герона:
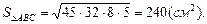
Но 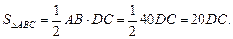
Из этих равенств находим 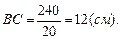 Подставляя найденные значения, получаем:
Подставляя найденные значения, получаем:
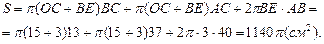
Таким образом, площадь поверхности тела вращения равна 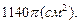
Ответ: 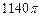 см2.
см2.
Пример 5. Два конуса имеют общую высоту, но вершины их лежат в разных концах высоты. Образующая первого конуса равна l, а угол при вершине его осевого сечения равен 2a. Угол при вершине осевого сечения второго конуса равен 2b.Найти объем общей части конусов.
Решение.Сделаем рисунок (рис. 39).
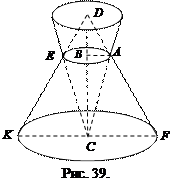
Объем общей части конусов равен сумме объемов конуса с общим основанием радиуса ВА, высотой BD и высотой BC соответственно. Получим следующее выражение для вычисления объема:
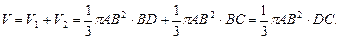
Рассмотрим первый конус, у которого образующая DF равна l, а угол при вершине осевого сечения 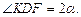 Треугольник CDF прямоугольный,
Треугольник CDF прямоугольный, 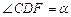 ,
, 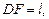 тогда
тогда 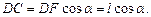 Из треугольника BDA (
Из треугольника BDA ( 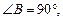
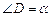 ) выразим DB:
) выразим DB: 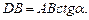 из треугольника BCA (
из треугольника BCA ( 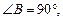
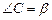 ) выразим BC:
) выразим BC: 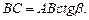
Получим следующее: 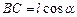 или
или 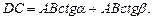 Из этих равенств выразим AB:
Из этих равенств выразим AB: 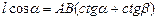 Þ
Þ 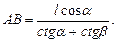
Подставив найденные выражения в формулу для вычисления объема, получим:
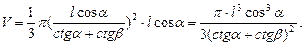
Ответ: 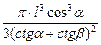 .
.
Дата добавления: 2016-07-27; просмотров: 20556;











