Дифракція на щілині в паралельних променях
Під час перпендикулярного падіння світла на площину щілини шириною 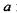 всі точки фронту хвилі.
всі точки фронту хвилі. 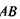 коливаються в однаковій фазі. Тому промені, які не змінили свого напрямку, не мають різниці ходу і, фокусуючись лінзою в точці
коливаються в однаковій фазі. Тому промені, які не змінили свого напрямку, не мають різниці ходу і, фокусуючись лінзою в точці 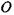 екрана, дають максимум освітленості (рис. 6.9).
екрана, дають максимум освітленості (рис. 6.9).
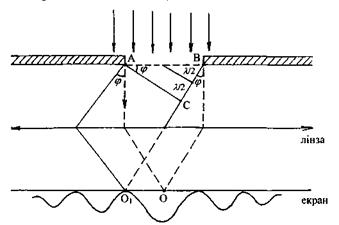
Рис. 6.9. Дифракція на щілині в паралельних променях.
Промені, які внаслідок дифракції відхилились на кут 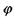 від напрямку променів, що падають на щілину, набувають різницю ходу
від напрямку променів, що падають на щілину, набувають різницю ходу 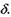 Визначимо цю різницю ходу, побудувавши фронт хвилі для цих променів. Для цього з точки
Визначимо цю різницю ходу, побудувавши фронт хвилі для цих променів. Для цього з точки 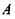 опустимо перпендикуляр на промінь, що виходить з точки
опустимо перпендикуляр на промінь, що виходить з точки 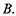 Очевидно, що різниця ходу
Очевидно, що різниця ходу 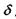 дорівнює довжині відрізка
дорівнює довжині відрізка 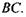 Розіб'ємо
Розіб'ємо 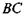 на відрізки величиною
на відрізки величиною 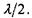 Якщо провести з точок поділу прямі паралельні.
Якщо провести з точок поділу прямі паралельні. 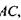 фронт хвилі в щілині
фронт хвилі в щілині 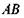 виявиться поділеним на зони, які називаються зонами Френеля. Вторинні хвилі, що йдуть від симетричних точок сусідніх зон Френеля, гасять одна одну. Для даних ширини щілини
виявиться поділеним на зони, які називаються зонами Френеля. Вторинні хвилі, що йдуть від симетричних точок сусідніх зон Френеля, гасять одна одну. Для даних ширини щілини 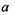 і довжини хвилі
і довжини хвилі 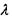 кількість зон
кількість зон 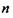 залежить від кута
залежить від кута 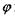 відхилення променів
відхилення променів
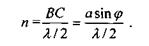 (6.7)
(6.7)
Число 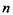 може бути парним і непарним. Якщо
може бути парним і непарним. Якщо 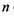 - парне число, то результатом інтерференції вторинних хвиль буде мінімум, оскільки в кожних двох сусідніх зонах маємо симетрично розташовані промені з
- парне число, то результатом інтерференції вторинних хвиль буде мінімум, оскільки в кожних двох сусідніх зонах маємо симетрично розташовані промені з 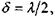 котрі, інтерферуючи в точці
котрі, інтерферуючи в точці 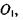 гасять один одного. Таким чином, напрямок на мінімум визначається умовою
гасять один одного. Таким чином, напрямок на мінімум визначається умовою 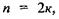 де
де 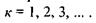 Враховуючи (6.7), маємо
Враховуючи (6.7), маємо 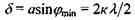 або
або
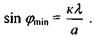 (6.8)
(6.8)
Якщо 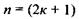 (остання зона може бути і неповною),
(остання зона може бути і неповною),
то в точці 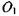 спостерігатиметься максимум, тобто напрямок на максимум визначається умовою або
спостерігатиметься максимум, тобто напрямок на максимум визначається умовою або 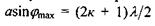
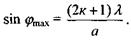 (6.9)
(6.9)
З формули (6.9) маємо: 1) за умови 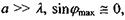 тобто кут дифракції
тобто кут дифракції 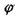 малий, і явище дифракції важко спостерігати; 2) за умови
малий, і явище дифракції важко спостерігати; 2) за умови 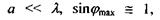 звідки
звідки 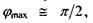 тобто весь екран буде освітленим і не спостерігатиметься чергування максимумів і мінімумів.
тобто весь екран буде освітленим і не спостерігатиметься чергування максимумів і мінімумів.
Очевидно, що для спостерігання дифракційної картини необхідне виконання умови 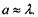
Дата добавления: 2020-11-18; просмотров: 630;











