РОЗДІЛ 2. ЕЛЕКТРОДИНАМІКА МЕДИКО-БЮЛОГІЧНИХ СИСТЕМ
"Хімія і вчення про магнетизм одне за одним визнали провідне значення електрики, і досить {Імовірно, що всі явища, які виникають під дією сил неорганічної матерії, а, можливо, й більшість тих, що стосуються рослинного та тваринного життя, виявляться врешті-решт їй підпорядкованими".
Майкл Фарадей
Класична електродинаміка - розділ фізики, що вивчає закономірності поведінки електромагнітного поля та його складових - електричного і магнітного полів. Електромагнітна взаємодія є дуже важливою через широту та різноманітність її проявів.
Електромагнітні явища мають, окрім свого великого теоретичного значення для розуміння процесів у живій та неживій природі, також і важливі медико-біологічні застосування, серед яких варто виділити:
· дослідження електричних процесів, що відбуваються в живих організмах, а також електричних та магнітних властивостей біологічних об'єктів;
· вивчення механізмів взаємодії зовнішніх електромагнітних полів з біологічними тканинами;
· використання сучасної електронної апаратури для потреб медицини та біології.
До вивчення основних законів електродинамічних процесів, що відбуваються в біологічних об'єктах, ми й переходимо.
ЕЛЕКТРОСТАТИКА
2.1.1. Основні характеристики електричного поля
Електричне поле - це поле, яке створюється електричними зарядами і здійснює взаємодію між ними. Частинним випадком є електростатичне поле; воно створюється нерухомими електричними зарядами, величина яких не змінюється з плином часу. Електричне поле можна виявити та дослідити за його дією на інші електричні заряди. З цією метою використовують пробні заряди, величина та розміри яких настільки малі, що вони не викликають перерозподілу зарядів в оточуючих тілах, а, отже, не спотворюють досліджуване поле.
Силовою характеристикою електричного поля є, як відомо, напруженість Е - векторна величина, яка дорівнює відношенню сили, що діє з боку поля на розміщений в даній точці пробний заряд q, до величини цього заряду:
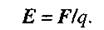 (2.1)
(2.1)
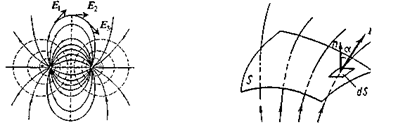
Мал. 2.1. Мал. 2.2.
Розмірність напруженості електричного поля в системі СІ: [Е] = Н/Кл = В/м. Графічно електричне поле зображують за допомогою ліній напруженості (силових ліній). Силові лінії - лінії, дотичні до яких в кожній точці електричного поля збігаються з вектором напруженості у цій точці. Силові лінії електростатичного поля незамкнені: вони починаються на позитивних зарядах і закінчуються на негативних або продовжуються у нескінченність (мал. 2.1). Густота
силових ліній, тобто їх число на одиницю площі, пропорційна до модуля напруженості.
Скалярну фізичну величину, яка дорівнює dN = E*dS*cosα, називають потоком вектора напруженості електричного поля через поверхню площею dS. Тут 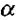 - кут, утворений вектором нормалі до поверхні п і вектором Е (мал. 2.2).
- кут, утворений вектором нормалі до поверхні п і вектором Е (мал. 2.2).
Поряд з напруженістю для характеристики електричного поля використовують ще одну векторну величину -електричну індукцію D. Електрична індукція не залежить від діелектричних властивостей середовища, а отже, не змінюється при переході з одного середовища в інше. Для поля у вакуумі:
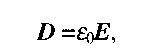 (2.2)
(2.2)
де 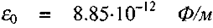 - абсолютна діелектрична
- абсолютна діелектрична
проникність вакууму (електрична стала).
Для ізотропного середовища з відносною діелектричною проникністю ε
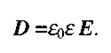 (2.3)
(2.3)
Розмірність електричної індукції в системі СІ: [D] =(Кл2/Н*м2)*Н/Кл = Кл/м2.
Електростатичне поле потенціальне, тобто робота його сил по переміщенню електричного заряду q між двома точками не залежить від форми траєкторії, а визначається лише початковим та кінцевим положеннями заряду. Як відомо, робота сил потенціального поля дорівнює зменшенню потенціальної енергії:
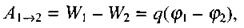 (2.4)
(2.4)
де ф - потенціал. Потенціал - скалярна фізична величина, яка характеризує здатність поля здійснювати роботу і визначається відношенням потенціальної енергії пробного заряду, вміщеного в дану точку поля, до величини цього заряду
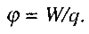 (2.5)
(2.5)
Розмірність потенціалу: 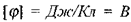 . Безпосередній фізичний зміст має не сам потенціал, оскільки він, як і потенціальна енергія, визначається з точністю до сталого доданка, а різниця потенціалів. Різниця потенціалів U називається напругою:
. Безпосередній фізичний зміст має не сам потенціал, оскільки він, як і потенціальна енергія, визначається з точністю до сталого доданка, а різниця потенціалів. Різниця потенціалів U називається напругою:
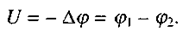 (2.6)
(2.6)
Геометричне місце точок, що мають однаковий потенціал, називають еквіпотенціальною поверхнею (на мал. 2.1 зображені пунктирними лініями). При переміщенні заряду вздовж еквіпотенціальної поверхні 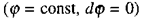 робота над зарядом не виконується. Це означає, що сили електричного поля, а отже, і лінії напруженості перпендикулярні до еквіпотенціальних поверхонь.
робота над зарядом не виконується. Це означає, що сили електричного поля, а отже, і лінії напруженості перпендикулярні до еквіпотенціальних поверхонь.
Зв'язок між напруженістю і потенціалом. Розглянемо переміщення позитивного точкового заряду dl на достатньо малу відстань з точки 1 в точку 2, на якій силу 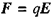 можна вважати постійною (мал. 2.3). Тоді робота
можна вважати постійною (мал. 2.3). Тоді робота
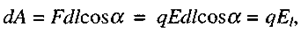 (2.7)
(2.7)
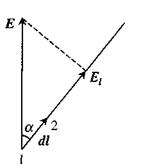
Мал. 2.3
де а - кут між векторами переміщення та сили. Припустимо, що через - точки 1 та 2 проходять еквіпотенціальні поверхні з потенціалами 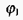 та
та 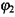 , тому з іншого боку згідно з (2.4)
, тому з іншого боку згідно з (2.4)
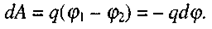 (2.8)
(2.8)
Прирівнявши цей вираз та (2.7), матимемо:
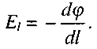 (2.9)
(2.9)
Це рівняння виражає зв'язок напруженості електричного поля з потенціалом: проекція вектора напруженості поля на заданий напрям дорівнює швидкості зменшення потенціалу в цьому напрямі. Можна сказати, що вектор напруженості електричного поля в будь-якій точці дорівнює градієнту потенціали, взятому зі знаком "-".
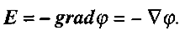 (2.10).
(2.10).
Таким чином, вектор напруженості електричного поля збігається з напрямком найбільшої зміни потенціалу. Знак "-" у формулі (2.10) показує, що вектор Е спрямований в бік зменшення потенціалу.
Якщо поле однорідне (Е - const), то остання формула набирає вигляду, відомого з шкільного курсу фізики:
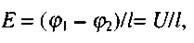 (2.11)
(2.11)
де l - відстань вздовж напрямку Е між точками з потенціалами 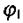 та
та 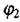
Принцип суперпозиції електричних полів.Розглянемо сукупність точкових електричних зарядів 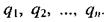 Кожний із цих зарядів створює власне електричне поле Е, незалежно від наявності інших зарядів. Для знаходження результуючого електричного поля в заданій точці застосовується принцип суперпозиції, який полягає в тому, що електричні поля окремих зарядів складаються. Напруженість Е результуючого електричного поля системи точкових зарядів визначається векторною сумою напруженостей полів еі, створених окремими зарядами:
Кожний із цих зарядів створює власне електричне поле Е, незалежно від наявності інших зарядів. Для знаходження результуючого електричного поля в заданій точці застосовується принцип суперпозиції, який полягає в тому, що електричні поля окремих зарядів складаються. Напруженість Е результуючого електричного поля системи точкових зарядів визначається векторною сумою напруженостей полів еі, створених окремими зарядами:
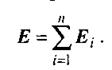 (2.12)
(2.12)
Потенціал результуючого поля (р дорівнює алгебраїчній сумі потенціалів % полів, створених окремими точковими зарядами:
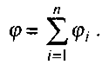 (2.13)
(2.13)
Формули (2.12) та (2.13) використовують для обчислення напруженості та потенціалу електричного поля, створеного будь-якими зарядженими тілами.
Електричний диполь
Вивчення цього питання має практичне значення, оскільки молекули багатьох речовин є природними диполями. Крім того, окремі органи та біологічні тканини в процесі своєї життєдіяльності створюють електричні поля, схожі з полем диполя. В даному параграфі розглянемо як поле диполя, так і поведінку диполя в зовнішньому електричному полі.
Диполем називають сукупність двох рівних за величиною точкових зарядів q протилежного знака, що знаходяться один від одного на малій відстані l , яку називають плечем диполя. Плечу диполя присвоюють напрямок від заряду -q до заряду +q (мал. 2.4). Лінія, що проходить через електричні заряди, називається віссю диполя. Основна характеристика диполя - електричний (дипольний) момент.
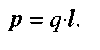 (2.14)
(2.14)
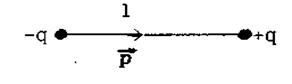
Мал. 2.4.
Електричний момент диполя вимірюють в кулон-метрах ([р] = Кл-м), а дипольні моменти молекул з причини їхніх малих значень - в позасистемних одиницях - Дебаях (Ц): 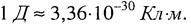 Поле, створене диполем.Диполь, в цілому електричне нейтральний, утворює навколо себе електричне поле. На мал. 2.1 зображена картина силових ліній та еквіпотенціальних поверхонь такого поля.
Поле, створене диполем.Диполь, в цілому електричне нейтральний, утворює навколо себе електричне поле. На мал. 2.1 зображена картина силових ліній та еквіпотенціальних поверхонь такого поля.
Знайдемо вираз для потенціалу поля, створеного диполем у деякій віддаленій 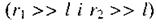 точці простору А (мал. 2.5). Оскільки для точкового заряду
точці простору А (мал. 2.5). Оскільки для точкового заряду 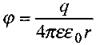 згідно з принципом суперпозиції (2.13) маємо:
згідно з принципом суперпозиції (2.13) маємо:
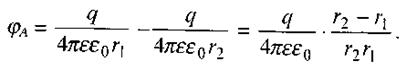 (2.15)
(2.15)
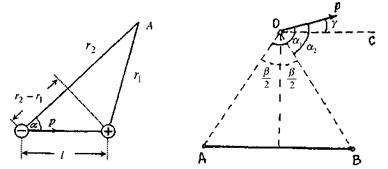
Мал. 2.5. Мал. 2.6.
Враховуючи, що відстані до точки А від зарядів 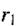 і
і 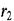 набагато більші за плече диполя /, можна записати
набагато більші за плече диполя /, можна записати 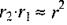 ;
;
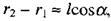 де α- кут між векторами р і r2. Підставивши ці вирази в (2.15), матимемо:
де α- кут між векторами р і r2. Підставивши ці вирази в (2.15), матимемо:
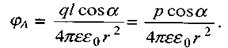 (2.16)
(2.16)
Застосуємо формулу (2.16) для знаходження різниці потенціалів між двома рівновіддаленими від диполя точками А і В (мал. 2.6).
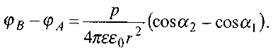
Проведемо через точку 0 пряму, паралельну до АВ. Нехай γ- кут утворений цією прямою і вектором p, тоді 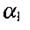
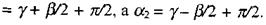 Звідки
Звідки
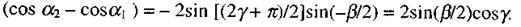
Отже,
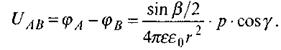 (2.17)
(2.17)
Таким чином, ми бачимо, що різниця потенціалів у двох рівновідцалених від диполя точках пропорційна проекції моменту диполя на пряму, що сполучає ці точки, і залежить від синуса половини кута, під яким видно ці точки.
Отриманий результат дозволяє встановлювати залежність між різницею потенціалів в двох точках поля і параметрами диполя (орієнтацією в просторі, величиною р) і використовується при реєстрації біопотенціалів в електрографії (кардіографії, енцефалографії, міографії тощо).
Диполь в електричному полі.Розглянемо спочатку поведінку диполя в однорідному електричному полі напруженості Е = const. На заряди диполя діє пара сил: 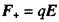 та
та 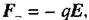 яка створює обертальний момент (мал. 2.7). Величина цього моменту визначається за формулою:
яка створює обертальний момент (мал. 2.7). Величина цього моменту визначається за формулою:
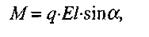 (2.18)
(2.18)
де 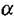 - кут між векторами Е і р. Таким чином, електричне поле намагається зорієнтувати диполь так, щоб вектори р і Е були співнапрямленими.
- кут між векторами Е і р. Таким чином, електричне поле намагається зорієнтувати диполь так, щоб вектори р і Е були співнапрямленими.
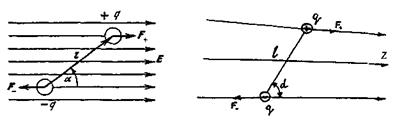
Мал. 2.7. Мал. 2.8.
У неоднорідному полі, де напруженість змінюється від точки до точки, диполь не тільки орієнтується вздовж ліній напруженості, а й втягується в область більшої напруженості. Це відбувається за рахунок нерівності сил 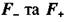 , які діють на позитивний та негативний заряди (мал. 2.8). Чим більша неоднорідність поля (більший градієнт напруженості), тим більша результуюча сила, яка діє на диполь:
, які діють на позитивний та негативний заряди (мал. 2.8). Чим більша неоднорідність поля (більший градієнт напруженості), тим більша результуюча сила, яка діє на диполь:
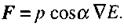 (2.19)
(2.19)
Сила F спрямована у бік більшої напруженості і досягає максимального значення, коли 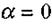 , тобто коли диполь розміщений вздовж лінії напруженості поля. Існуванням цієї сили пояснюється притягання наелектризованою скляною чи ебонітовою паличкою легких предметів, налипання пилу на наелектризовані поверхні. За рахунок цього ефекту іони в рідких та газоподібних середовищах з полярними молекулами створюють оболонку з молекулярних диполів.
, тобто коли диполь розміщений вздовж лінії напруженості поля. Існуванням цієї сили пояснюється притягання наелектризованою скляною чи ебонітовою паличкою легких предметів, налипання пилу на наелектризовані поверхні. За рахунок цього ефекту іони в рідких та газоподібних середовищах з полярними молекулами створюють оболонку з молекулярних диполів.
Дата добавления: 2020-11-18; просмотров: 709;











