При плоском поперечном изгибе (задачи № 12–15)

Рекомендуемая литература

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 2 (§ 2.5).

Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 5 (§ 22).

Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 7 (§ 7.1–7.5).

Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений из уравнений отсеченной части балки следует, что поперечную силуможно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент численно равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).

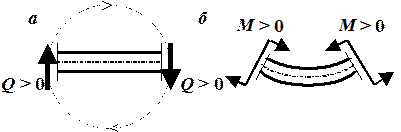Рис. 4.5. Правило знаков: а – для поперечной силы; б – для изгибающего момента в балке

Введем правила знаков для поперечной силы и изгибающего момента. Поперечная сила считается положительной, если она обходит сечение по часовой стрелке (т. е. сила, находящаяся слева от сечения и направленная вверх, или сила, находящаяся справа от сечения и направленная вниз, – положительны) (рис. 4.5, а).Изгибающий момент положителен, если он изгибает балку выпуклостью вниз. Обращаем внимание на то, что знак внутреннего усилия – изгибающего момента – зависит от того, с какой стороны от сечения находится момент[3]. Как видно из рис. 4.5, б момент, находящийся слева от сечения, действует по часовой стрелке, а момент, расположенный справа от сечения, – против часовой стрелки. И оба они положительны.

При построении эпюр Q и М договоримся на эпюре Q положительные значения откладывать сверху нулевой линии. На эпюре М у строителей принято откладывать положительные ординаты снизу. Такое правило построения эпюры М называется построением эпюры со стороны растянутых волокон, т. е. положительные значения М откладываются в сторону выпуклости изогнутой балки.

Известно [2], что изгибающий момент М, поперечная сила и интенсивность распределенной нагрузки q связаны между собой такими дифференциальными зависимостями:

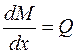, (4.11)

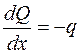(4.12)

и, как следствие (4.11) и (4.12),

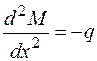. (4.13)

При выводе формул (4.11)–(4.13) нагрузка 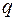считалась положительной, если она направлена вниз.

Из определений для поперечной силы и изгибающего момента, а также из дифференциальных зависимостей (4.11)–(4.13) вытекают следующие правила проверки правильности построения эпюр Q и М:

На эпюре Q под сосредоточенной силой имеет место скачок на величину этой силы. На эпюре М в этом сечении должен быть перелом, т. е. резкое изменение угла наклона прямой (или касательной к кривой).

На эпюре М скачок имеет место под сосредоточенной парой на величину этой пары.

Из зависимостей (4.11), (4.12) можно определить вид функций Q и М:

· если на участке отсутствует распределенная нагрузка (q = 0), то 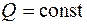, а М – линейная функция x;

· если на участке действует равномерно распределенная нагрузка (q = const), то Q – линейная функция, а М – квадратная парабола;

· если на участке действует линейно распределенная нагрузка, то соответственно Q является квадратной параболой, а М – кубической.

3. Характер поведения функции на участке (то есть ее возрастание или убывание) зависит, как известно, от знака первой производной функции. И из дифференциальных зависимостей (4.11), (4.12) следует:

· если на участке распределенная нагрузка q > 0 (действует вниз), то поперечная сила Q на этом участке является убывающей функцией;

· если на участке поперечная сила положительна, то функция М(x) возрастает;

· если на участке в каком-то сечении 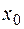функция 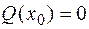, то на эпюре М в этом сечении имеет место экстремум.

4. По знаку второй производной функции определяется выпуклость функции. Из зависимости (4.13) вытекает, что эпюра М всегда имеет выпуклость в сторону действия распределенной нагрузки (q – вниз, выпуклость – вниз и наоборот). По знаку второй производной от Q можно определить выпуклость эпюры Q. Из (4.11)

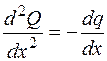
и, если q(x) – возрастающая функция, то 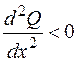и эпюра Q имеет выпуклость вверх.

6. Из (4.11) следует, что

.

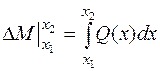Это означает, что приращение изгибающего момента DМ на участке между сечениями х₁ и х₂ равно площади эпюры Q на указанном участке.

7. Из (4.12) получим:

.

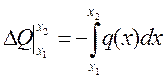То есть приращение поперечной силы 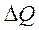на участке между сечениями х₁ и х₂ равно площади графика 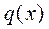на этом участке. Например, если нагрузка q является равномерно распределенной, то площадь графика q равна 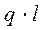, где l – длина участка, на котором действует q.

Примечание. Зависимости (4.11) и (4.12) и перечисленные правила справедливы, если начало отсчета x вести слева направо и эпюру М строить со стороны растянутых волокон.

Рекомендуем после построения эпюр обязательно проанализировать результаты, проверив выполняются ли все перечисленные правила в решенной Вами задаче.

Пример 1

Условие задачи

Рис. 4.6. К решению примера 1 по построению эпюр Q и М: а – схема балки с нагрузками; б – эпюры поперечной силы и изгибающего момента

Дана балка с действующими на нее нагрузками (рис. 4.6, а). Требуется определить внутренние усилия – поперечную силу Q и изгибающий момент М в балке, построить графики их изменения вдоль оси стержня (эпюры Q и М).

Решение

Прежде всего, найдем опорные реакции. Балка имеет жесткое защемление на правом конце[4] и в этом закреплении при заданной вертикальной нагрузке возникают две опорные реакции: вертикальная реакция R_A и реактивный момент M_A. Горизонтальная реакция при действии вертикальной нагрузки равна нулю. Это следует из уравнения равновесия "сумма проекций всех сил на горизонтальную ось равна нулю". Определим R_A и M_A, используя два других уравнения статики. Желательно составлять такие уравнения, в каждое из которых входит только одна неизвестная. В данном случае такими уравнениями являются "сумма проекций всех сил на вертикальную ось (ось z) равна нулю" и "сумма моментов всех сил относительно точки А равна нулю":

; ;

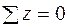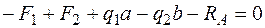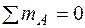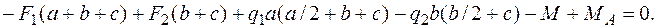; Из первого уравнения найдем R_A = 30 кН, из второго – М_А =5 кН×м. Полученные положительные знаки опорных реакций подтверждают выбранные нами направления опорных реакций: R_A – вверх, а М_А – против часовой стрелки. Для проверки рекомендуем использовать любое другое уравнение равновесия, например :

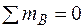– 30×2 – 15×2×1 – 60 + 10×1×2,5 + 30×4+5 = – 150 + 150 = 0.

Теперь определяем внутренние усилия: поперечную силу Q и изгибающий момент М. В соответствии с методом сечений рассекаем балку на каждом участке (в данной задаче их три) произвольным сечением и рассматриваем все силы, расположенные с одной стороны от сечения: слева или справа. Удобно рассматривать все силы с той стороны от сечения, где сил меньше. Начало отсчета координаты x на каждом участке можно выбирать произвольным образом. Например, на рис. 4.6, а начало отсчета x на каждом участке – свое и находится в начале участка. Запишем выражения для Q и М на каждом участке.

Участок 1: .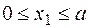

Рассмотрим силы, расположенные слева от сечения. По определению поперечной силы и с учетом правила знаков для Q (см. рис. 4.5, а):

.

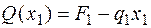Здесь 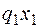– равнодействующая равномерно распределенной нагрузки, действующей слева от сечения.

По определению изгибающего момента и с учетом правила знаков для М (см. рис. 4.5, б):

,

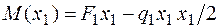где во втором слагаемом 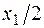– плечо равнодействующей равномерно распределенной нагрузки ( 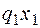), взятой слева от сечения (равнодействующая приложена по середине длины отсеченной части балки x₁).

Для построения эпюр найдем значения Q и М на границах участка:

в начале участка (х₁ = 0) 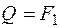, а ;

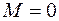в конце участка ( ) ; .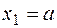

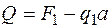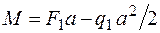Участок 2: .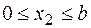

Снова рассмотрим все силы, расположенные слева от сечения.

;

.

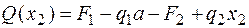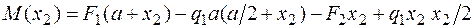Граничные значения Q и М:

в начале участка ( ) ;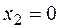

,

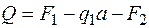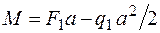в конце участка ( ) ;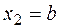

.

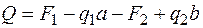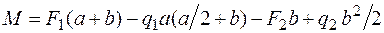Участок 3: .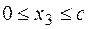

Теперь рациональнее рассмотреть все силы справа от сечения. Тогда

;

.

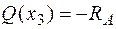Из этих выражений следует, что поперечная сила на третьем участке – постоянная величина, а изгибающий момент меняется по линейному закону и на границах участка имеет следующие значения:

в начале участка ( ) ,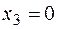

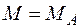в конце участка ( ) .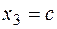

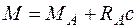Запишем результаты определения внутренних усилий в таблицу, сосчитав численные значения Q и М на границах участков (табл. 1).

Таблица 1

Из таблицы видно, что поперечная сила на первом участке меняет свой знак, т. е. график Q пересекает нулевую линию. Это значит, что изгибающий момент на этом участке имеет экстремум. Найдем максимальное значение М на этом участке. Сначала определим то значение координаты х₁, при котором поперечная сила равна нулю. Обозначим это значение координаты х₀ (см. рис. 4.6).

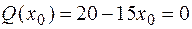х₀ = 1,33 м.

Чтобы найти максимальное значение изгибающего момента, подставим х₀ в выражение для М на первом участке:

кН×м.

По результатам вычислений в таблице строим эпюры Q и М на каждом участке (см. рис. 4.6, б). Не забываем после построения эпюр проанализировать результаты по тем правилам проверки правильности построения эпюр, которые перечислены ранее.

Пример 2

Условие задачи

На балку кроме равномерно распределенной нагрузки действует линейно распределенная (треугольная) нагрузка (рис. 4.7, а). Построим эпюры распределения поперечной силы и изгибающего момента, обращая внимание на определение Q и М на участке с треугольной нагрузкой.

Решение

Найдем опорные реакции. Балка имеет шарнирное опирание и для определения двух не равных нулю опорных реакций R_A и R_B (горизонтальная реакция H_A = 0) составим два независимых уравнения статики. Рациональными уравнениями, в каждое из которых входит одна неизвестная реакция, в данном случае являются:

; ,

; .

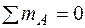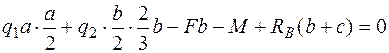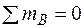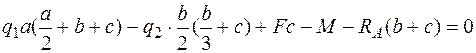Напомним как определяется момент от треугольной нагрузки. Равнодействующая от треугольной нагрузки равна площади треугольника 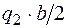и приложена в центре тяжести треугольника, поэтому плечо этой равнодействующей относительно точки А равно 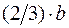, а относительно точки В – 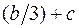. Из этих уравнений найдем R_A = – 31,9 кН, R_B = – 18,1 кН. Отрицательные знаки показывают, что обе реакции направлены не вверх, как показано на рис. 4.7, а, а в противоположную сторону. Для проверки опорных реакций составим уравнение равновесия "сумма проекций сил на вертикальную ось z равна нулю":

; .

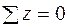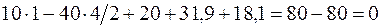Определение внутренних усилий производим, записывая выражения для Q и М в таблицу (табл. 2).

Поясним выражения для Q и М на втором участке, а именно третьи слагаемые в этих выражениях, учитывающие треугольную нагрузку. Чтобы найти равнодействующую от треугольной нагрузки, расположенной слева от рассматриваемого сечения на участке длиной х₂, определим интенсивность распределенной нагрузки в сечении х₂, которая на рис. 4.7, а обозначена 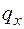. Для этого составим пропорцию: 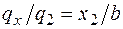, откуда 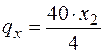. Тогда равнодействующая этой распределенной нагрузки на участке длиной х₂ 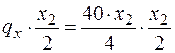. Она приложена в центре тяжести треугольника, и изгибающий момент, создаваемый этой нагрузкой, равен 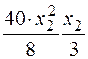, где 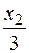– плечо равнодействующей.

Таблица 2

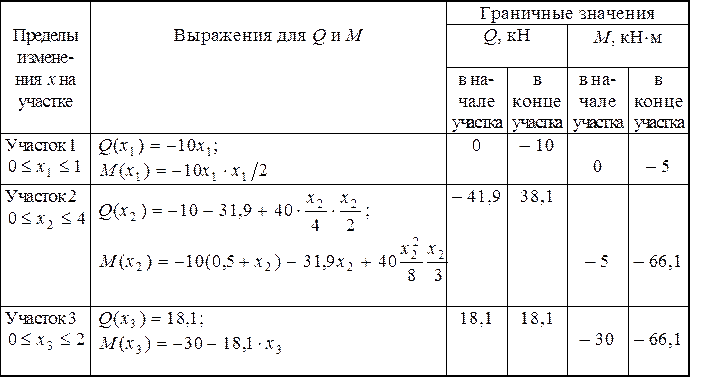
Поскольку поперечная сила на втором участке меняет знак, найдем экстремальное значение изгибающего момента в сечении х₀на этом участке (рис. 4.7, б). Определим величину х₀, приравняв выражение для поперечной силы на втором участке нулю:

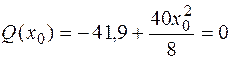, откуда х₀ = 2,89 м. Тогда

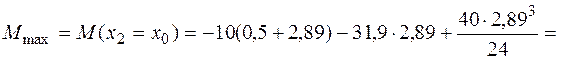
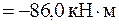
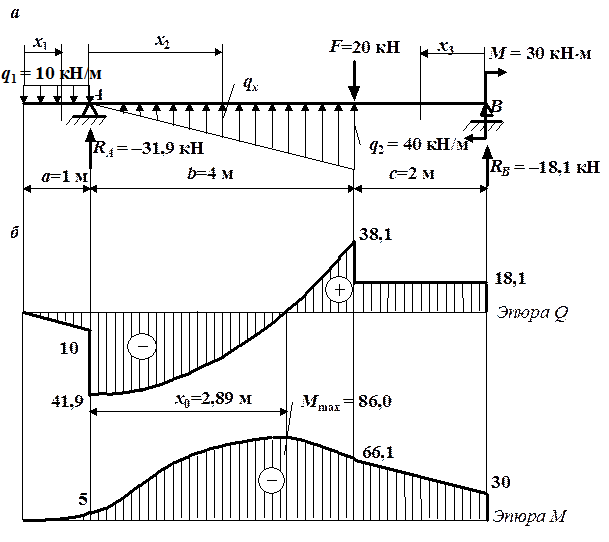Рис. 4.7. К решению примера 2 по построению эпюр Q и М: а – схема балки с нагрузками; б – эпюры поперечной силы и изгибающего момента

По полученным в таблице выражениям строим эпюры внутренних усилий. Напомним, что выпуклость эпюры М направлена в сторону распределенной нагрузки. Выпуклость эпюры Q на втором участке можно определить по знаку второй производной 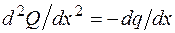. В данном случае функция 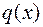является убывающей, следовательно 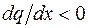, а 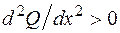. Это означает, что эпюра Q имеет выпуклость вниз. Можно определить выпуклость эпюры поперечной силы и по-другому. В сечении, где интенсивность распределенной нагрузки равна нулю (начало второго участка в данной задаче), угол наклона касательной к кривой Q(x) должен равняться нулю, так как в этом сечении 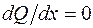. Это возможно тогда, когда функция Q(x) имеет выпуклость вниз.

После того, как Вы нарисовали эпюры, рекомендуем обязательно проанализировать их по правилам проверки правильности построения эпюр.