Статистические способы выявления связи.
Выявление и измерение связи статистика осуществляет при помощи различных методов. Важнейшими из них являются: метод сопоставления параллельных рядов, балансовый метод, метод группировок, метод корреляционного анализа.
Способ сопоставления параллельных рядов – элементарный, но широко распространенный и весьма эффективный способ выявления связи. Параллельные ряды – это табличная форма изображения статистических данных по развитию признаков изучаемых явлений. Наглядным подтверждением эффективности способа сопоставления параллельных рядов может служить следующий пример.
Основные показатели деятельности подрядных строительно-монтажных организаций
| Показатели | Годы | |||
| Объем подрядных работ, выполненных собственными силами, д.е. | 83,2 | 95,3 | 110,9 | 106,1 |
| Число строительно-монтажных управлений и приравненных к ним организаций (на конец года), тыс.ед. | 3,3 | 3,5 | 3,5 | 3,4 |
| Среднегодовая численность работников, занятых в строительстве, тыс. чел. |
Из таблицы видно, что с увеличением числа строительно-монтажных трестов и численности работников, занятых в строительстве, увеличивается и объем подрядных работ, а с уменьшением факторных признаков (2005г.) – уменьшается и результативный.
Балансовый метод находит также широкое применение в практике выявления и характеристики связи между явлениями. Этот метод сводится к построению таблиц, в которых излагаются данные по взаимосвязанным показателям. Основой каждого баланса является балансовое уравнение. Балансовые сопоставления производятся в стоимостной и натуральной форме.
Балансовый метод используется для выявления взаимосвязи между отраслями народного хозяйства, между производством и потреблением, для характеристики межрегиональных связей, широко используются материальные балансы и т.д. Балансовый метод позволяет так же произвести увязку и контроль взаимосвязанных показателей. Например, баланс населения – это система показателей, характеризующая процесс и результат воспроизводства населения. Общая схема баланса населения следующая:
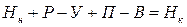 , где
, где
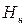 - численность населения на начало периода;
- численность населения на начало периода;
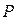 - число родившихся за период;
- число родившихся за период;
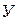 - число умерших за период;
- число умерших за период;
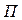 - число приехавших;
- число приехавших;
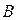 - число выехавших;
- число выехавших;
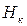 - численность населения на конец периода.
- численность населения на конец периода.
Данный баланс может быть использован для определения одного неизвестного компонента на основании других известных. Например, миграционный прирост (приехавшие минус выехавшие) можно найти следующим образом:
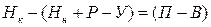
Примером более сложных балансовых построений могут служить балансы межотраслевых связей.
Метод группировок так же широко используется в анализе взаимосвязей. Он позволяет выявить наличие и охарактеризовать направление связи. Использование метода группировок в изучении связи между явлениями рассмотрено в теме «Сводка и группировка статистической информации».
3. Корреляционный метод анализа взаимосвязей.
Корреляционный анализ включает расчет целого ряда показателей.
Корреляционное отношение. Использование аналитических группировок дает возможность не только выявить наличие и направление связи между изучаемыми признаками, но и определить её тесноту. Показателем тесноты связи в этом случае может служить корреляционное отношение, рассчитываемое на основе правила сложения дисперсий:
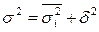 , где
, где
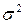 - общая дисперсия;
- общая дисперсия;
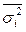 - средняя из групповых дисперсий (остаточная);
- средняя из групповых дисперсий (остаточная);
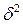 - межгрупповая дисперсия.
- межгрупповая дисперсия.
Из этого правила следует, что чем более признак-фактор, положенный в основу группировки, определяет изменение признака-результата, тем в большей степени величина межгрупповой дисперсии 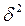 приближается по своим размерам к величине общей дисперсии
приближается по своим размерам к величине общей дисперсии 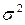 .
.
Если изменение результативного признака всецело определяется изменениями признака-фактора, т.е. при функциональной зависимости общая и межгрупповая дисперсии будут между собой равны, а средняя из групповых дисперсий равна нулю.
Если связь между признаками отсутствует, общая дисперсия будет равна средней из групповых, а межгрупповая – равна нулю.
Это значит, что отношение межгрупповой дисперсии к общей 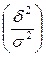 может быть использовано для оценки тесноты связи между изучаемыми признаками. Корень квадратный из этого отношения называется корреляционным отношением.
может быть использовано для оценки тесноты связи между изучаемыми признаками. Корень квадратный из этого отношения называется корреляционным отношением.
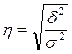
Абсолютные размеры корреляционного отношения колеблются от нуля до единицы. При отсутствии связи между признаками 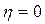 , при функциональной -
, при функциональной - 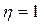 . Чем больше
. Чем больше 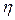 приближается к единице, тем теснее связь.
приближается к единице, тем теснее связь.
Корреляционное уравнение зависимости (Уравнение регрессии.) Нахождение уравнения корреляционной связи, его параметров (коэффициентов перед переменными), значений результативного признака по этому уравнению называют выравниванием, а вычисленные по нему значения результативного признака - выровненными значениями, которые обозначаются 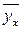 .
.
При прямолинейной связи это уравнение прямой:
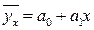 ,
,
где 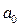 и
и 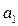 - параметры уравнения;
- параметры уравнения;
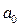 - постоянный;
- постоянный;
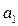 - средний переменный, изменяющийся пропорционально
- средний переменный, изменяющийся пропорционально 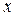 ;
;
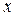 - значение признака-фактора;
- значение признака-фактора;
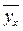 - выравненное значение результативного признака.
- выравненное значение результативного признака.
Параметры линейного корреляционного уравнения находят, используя метод наименьших квадратов из системы нормальных уравнений:
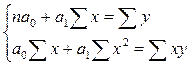
Если исходные данные сгруппированы, то система нормальных уравнений принимает следующий вид:
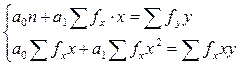
где f - частоты отдельных значений 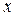 и
и 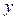 .
.
Следует отметить, что корреляционное уравнение имеет не абсолютное, а относительное значение, т.е. оно верно только относительно тех условий места и времени на основе данных, по которым оно рассчитано.
В другой ситуации оно может иметь другие параметры.
Корреляционное уравнение позволяет сделать вывод о направлении связи. Направление связи определяется знаком параметра 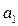 : если
: если 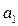 положительно – связь прямая, отрицательно – обратная. Численное значение
положительно – связь прямая, отрицательно – обратная. Численное значение 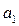 показывает, на сколько единиц изменяется значение результативного признака при изменении значения признака-фактора на единицу.
показывает, на сколько единиц изменяется значение результативного признака при изменении значения признака-фактора на единицу.
Индекс корреляции – показатель тесноты связи. Он рассчитывается по следующей формуле:
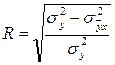
где 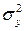 - общая дисперсия признака
- общая дисперсия признака 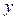 :
: 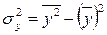 ;
;
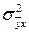 - средний квадрат отклонений значений результативного признака от выравненных его значений.
- средний квадрат отклонений значений результативного признака от выравненных его значений.
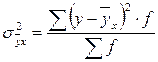 , а в случае не сгруппированных данных:
, а в случае не сгруппированных данных: 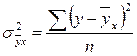 .
.
Индекс корреляции так же как и корреляционное отношение колеблется от нуля до единицы и характеризует только тесноту связи. При этом чем ближе индекс корреляции к единице, тем теснее связь, и чем ближе к нулю, тем связь слабее.
Направление связи определяется расчетом уравнения зависимости.
Линейный коэффициент корреляции. При линейной форме зависимости между признаками показатель тесноты связи можно рассчитать по формуле:
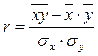
где 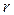 - линейный коэффициент корреляции;
- линейный коэффициент корреляции;
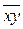 - средняя из произведений
- средняя из произведений 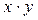 ;
;
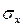 - среднее квадратическое отклонение признака
- среднее квадратическое отклонение признака 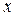 ;
;
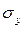 - среднее квадратическое отклонение признака
- среднее квадратическое отклонение признака 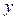 .
.
Линейный коэффициент корреляции может принимать значения от -1 до +1, т.е. может быть положительным и отрицательным. Следовательно, его расчет позволяет определить не только тесноту, но и направление связи между изучаемыми признаками, не прибегая к выравниванию. Если 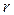 положителен – связь прямая, отрицателен – связь обратная. Чем ближе коэффициент корреляции к единице, тем теснее связь, чем ближе к нулю – тем слабее.
положителен – связь прямая, отрицателен – связь обратная. Чем ближе коэффициент корреляции к единице, тем теснее связь, чем ближе к нулю – тем слабее.
Расчет линейного уравнения связи, индекса корреляции и линейного коэффициента покажем на примере.
Пример.
Имеются следующие данные о квалификации и заработной плате рабочих.
| Табельный номер | ||||||||||
| Разряд | ||||||||||
| Заработная плата, тыс. руб. |
Для характеристики связи между рассматриваемыми признаками исчислить:
а) линейное корреляционное уравнение;
б) линейный коэффициент корреляции;
в) индекс корреляции.
Квалификация – факторный признак, обозначим его через 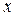 .
.
Заработная плата – результативный, обозначим - 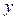 .
.
Линейное корреляционное уравнение имеет следующий вид:
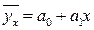 .
.
Для нахождения его параметров необходимо решить систему нормальных уравнений:
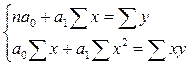 .
.
Линейный коэффициент корреляции исчислим по формуле:
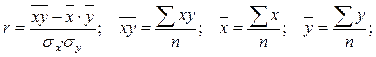
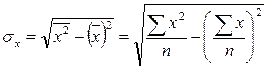 ;
;
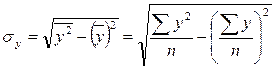 .
.
Для нахождения величин, входящих в данные уравнения и формулы составим следующую расчетную таблицу и заполним первые пять граф.
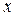
| 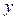
| 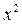
| 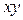
|  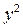
| 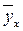
| 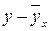
| 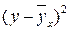
|
| 64,65 | -6,65 | 44,2 | |||||
| 73,30 | -9,30 | 86,5 | |||||
| 81,96 | 7,05 | 49,7 | |||||
| 90,60 | 7,40 | 54,76 | |||||
| 56,00 | 16,00 | 256,0 | |||||
| 47,35 | 1,65 | 2,72 | |||||
| 73,30 | -2,30 | 5,29 | |||||
| 64,65 | -5,65 | 31,9 | |||||
| 73,30 | -5,30 | 28,1 | |||||
| 64,65 | -2,65 | 7,0 | |||||
| ИТОГО | |||||||
| 689,75 | 566,2 |
В нашем примере система нормальных уравнений будет иметь следующий вид:
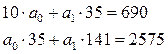
Решив данную систему, найдем параметры линейного корреляционного уравнения:
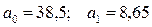
Для нашего примера линейное корреляционное уравнение имеет следующий вид:
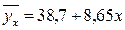
Это значит, что с повышением квалификации на один разряд, заработная плата возрастает в среднем на 8,65 тыс.рублей.
Для расчета линейного коэффициента корреляции определим:
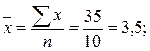
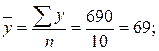
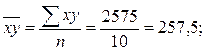
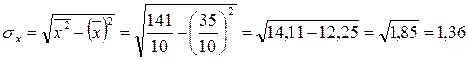
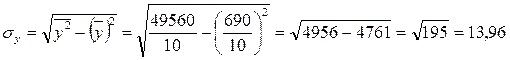
Тогда
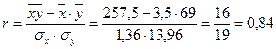
Это означает, что между размером заработной платы и уровнем квалификации рабочего существует тесная прямая связь.
Чтобы определить индекс корреляции, дополним расчетную таблицу тремя графами. Для заполнения графы 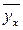 используем найденное выше уравнение регрессии:
используем найденное выше уравнение регрессии:
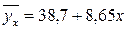
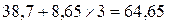
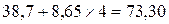
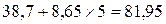
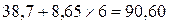
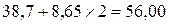
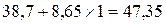
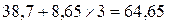
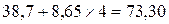
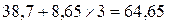
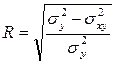
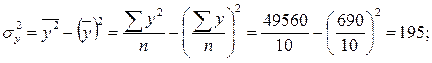
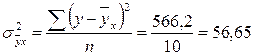 ;
;
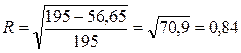 .
.
Индекс корреляции, равный 0,84, свидетельствует о тесной связи между заработной платой и уровнем квалификации рабочих.
Совпадение значений коэффициента корреляции и индекса корреляции свидетельствует о наличии прямой линейной зависимости заработной платы от уровня квалификации.
Дата добавления: 2020-10-25; просмотров: 511;











