Контрольное задание по теме 2.8. «Динамическое программирование».

Пусть расходы, связанные с приобретением и заменой оборудования по периодам, представлены в таблице, r – учетный процент в течение каждого периода. Определить срок замены оборудования без учета и с учетом коэффициента дисконтирования.

Таблица вариантов

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ

1. Эконометрическое моделирование функции спроса.

2. Эконометрическое моделирование функции предпочтения.

3. Эластичность спроса по цене: определение и использование в практике маркетинга.

4. Методы оценивания эластичности спроса по цене.

5. Свойства эластичности спроса по цене.

6. Предельные издержки и объем производства.

7. Перекрестные коэффициенты эластичности.

8. Уравнение Слуцкого.

9. Производственные функции затрат ресурсов.

10. Модели общего экономического равновесия.

11. Формальные требования к функции полезности лица, принимающего решения в условиях риска, и их экономические основания.

12. Представление рисков в экономико-математических моделях оптимального планирования.

13. Функция полезности Неймана-Моргенштерна: теоретические основы и практическое применение.

14. Понятие и математическая формализация потребительского выбора.

15. Использование моделей потребительского выбора для принятия управленческих решений.

16. Статистическая и динамическая модели межотраслевого баланса.

17. Модель равновесных цен.

18. Модель международной торговли.

19. Анализ и классификация основных математических моделей, применяемых при исследовании систем управления в экономике.

20. Этапы экономико-математического моделирования.

21. Задача линейного программирования и ее экономическая интерпретация.

22. Понятие устойчивости решения в задаче линейного программирования

23. Двойственная задача линейного программирования и объективно-обусловленные оценки.

24. Целочисленное линейное программирование.

25. Постановка транспортной задачи и математическая модель в общем виде.

26. Методы решения транспортной задачи.

27. Вырожденные случаи при решении транспортной задачи.

28. Область применения сетевых моделей.

29. Сетевая модель: основные элементы и правила построения топологии сети.

30. Временные параметры сетевой модели.

31. Алгоритм расчета временных параметров сетевой модели.

32. Методы оптимизации потребления ресурсов при управлении проектами.

33. Теоретические основы применения математических методов в логистике.

34. Формулировка и экономическая интерпретация классической задачи управления запасами.

35. Методика исследования классической задачи управления запасами.

36. Математические методы оптимизации стратегии пополнения запасов.

37. Математические методы регулирования товарных запасов в системах с фиксированным размером заказа.

38. Применение математических методов для регулирования товарных запасов в системах с фиксированной периодичностью заказа.

39. Оптимизация размеров заказа для создания товарных запасов.

40. Понятие и экономическая интерпретация системы массового обслуживания.

41. Использование теории очередей в управлении потоками товаров и услуг.

42. Расчёт средней длины очереди к системе массового обслуживания.

43. Расчёт вероятности превышения пороговой длины очереди к системе массового обслуживания.

44. Расчёт среднего времени ожидания в очереди к системе массового обслуживания.

45. Необходимое условие работоспособности системы массового обслуживания, его обоснование и экономическое значение.

46. Формулировка и экономическая интерпретация модели системы массового обслуживания.

47. Понятие и примеры матричных антагонистических игр с нулевой суммой.

48. Задача определения оптимальной смешанной стратегии в антагонистической матричной игре с нулевой суммой и её экономическая интерпретация.

49. Математические методы принятия управленческих решений в условиях конфликта.

50. Применение теории игр к проблемам антикризисного управления.

51. Компенсация рисков реализации инвестиционных проектов с использованием методов теории игр.

52. Понятие и экономическая интерпретация цены игры. Определение цены матричной антагонистической игры с нулевой суммой.

53. Оптимальные смешанные стратегии: понятие, причины использования, приёмы практической реализации.

54. Подготовка исходных данных для анализа матричной антагонистической игры с нулевой суммой в целях подготовки управленческого решения.

55. Принцип оптимальности Беллмана.

56. Классические примеры использования динамического программирования.

57. Понятие оптимума по Парето и его экономическая интерпретация.

58. Методы исследования многокритериальных математических моделей.

59. Методы отыскания частных оптимумов по Парето и условия их применимости.

ИТОГОВЫЕ ТЕСТЫ

1. Что выбирается в качестве показателя эффективности при возникновении форс-мажорных обстоятельств?

а) берется сама величина, которую хотелось бы минимизировать;

б) берется сама величина, которую хотелось бы максимизировать;

в) берется не сама величина, а ее среднее значение – математическое ожидание;

г) берется дисперсия самой величины;

д) все вышеназванное.

2. Какой показатель и критерий эффективности можно выбрать при снабжении предприятий сырьем?

а) суммарные расходы на перевозки сырья;

б) суммарные расходы на перевозки сырья за единицу времени;

в) минимальные расходы на перевозки;

г) максимальные расходы на сырье;

д) все вышеназванное.

3. Какой показатель и критерий эффективности можно выбрать при постройке участка магистрали?

а) время завершения стройки;

б) среднее ожидаемое время окончания стройки;

в) максимальное время окончания стройки;

г) минимальное время окончания стройки;

д) стоимость стройки.

4. Какой показатель и критерий эффективности можно выбрать при продаже сезонных товаров?

а) максимально ожидаемую прибыль;

б) среднюю ожидаемую прибыль от реализации товаров за сезон;

в) расходы при продаже;

г) максимальное время продажи;

д) все вышеназванное.

5. Какой показатель можно выбрать для характеристики эффективности работы городского транспорта?

а) среднюю скорость передвижения пассажиров по городу;

б) среднее число перевезенных пассажиров;

в) среднее количество километров, которое придется пройти пешком человеку, которого транспорт не может доставить в нужное место;

г) ни один из вышеназванных не подходит для этого;

д) все вышеназванные.

6. Из чего исходят в каждом конкретном случае при выборе модели экономических операций?

а) из вида операции;

б) из целевой направленности операций;

в) содержимое а и б;

г) из экономической ситуации;

д) все вышеперечисленное.

7. Какие разделы математики положены в основу исследования операций?

а) линейное, нелинейное, динамическое программирование;

б) теория игр;

в) теория статистических решений;

г) теория массового обслуживания;

д) все вышеперечисленное.

8. Почему при исследовании операций необходимы сведения по теории вероятности?

а) чтобы лучше соразмерять точность и подробность модели;

б) потому что большинство операций проводится в условиях неполной определенности, и их ход и исход зависят от случайных факторов;

в) потому что большинство операций проводится в условиях полной определенности, и их ход и исход не зависят от случайных факторов;

г) потому что большинство операций проводится в условиях неполной определенности, и их ход и исход не зависят от случайных факторов;

д) все вышеперечисленное.

9. Какие модели широко применяются в исследовании операций?

а) аналитические;

б) статистические;

в) имитационные;

г) пункты а и б;

д) пункты а, б и в.

10. В чем преимущества аналитических моделей при применении в исследованиях операций?

а) результаты расчета по ним легче обозримы;

б) отчетливее отражают присущие явлению основные закономерности;

в) больше приспособлены для поиска оптимальных решений;

г) содержимое п.а, б, в;

д) учитывают большее число факторов.

11. В чем преимущества статистических моделей при применении в исследованиях операций?

а) более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории – неограниченно большое) число факторов;

б) отчетливее отражают присущие явлению основные закономерности;

в) больше приспособлены для поиска оптимальных решений;

г) содержимое п.а, б, в;

д) учитывают большее число факторов.

12. В чем недостатки статистических моделей при применении в исследованиях операций?

а) громоздкость;

б) плохая обозримость;

в) большой расход машинного времени;

г) крайняя трудность поиска оптимальных решений, которые приходится искать “на ощупь”, путем догадок и проб;

д) все вышеперечисленное.

13. В чем недостатки аналитических моделей при применении в исследованиях операций?

а) более грубы;

б) учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений;

в) трудность поиска оптимальных решений;

г) содержимое п.а, б;

д) все вышеперечисленное.

14. В чем заключается особенность задач целочисленного программирования?

а) в том, что постановка задачи совпадает с постановкой задачи линейного программирования;

б) в том, что искомые значения переменных непременно должны быть целыми;

в) в том, что постановка задачи не совпадает с постановкой задачи линейного программирования;

г) в том, что постановка задачи совпадает с постановкой задачи динамического программирования;

д) в том, что искомые значения переменных непременно должны быть дробными.

15. В чем заключается задача распределения ресурсов по операциям?

а) в выборе такого распределения ресурсов по операциям, при котором достигается максимальная общая эффективность системы;

б) в выборе такого распределения ресурсов по операциям, при котором достигается минимальная общая эффективность системы;

в) в минимизации суммарных затрат или максимизации суммарной прибыли;

г) содержимое п.а, б;

д) содержимое п.б, в.

16. К чему сводится решение задач о назначении?

а) к выбору (назначению) по одному ресурсу для выполнения каждой операции;

б) к выбору (назначению) по множеству ресурсов для выполнения каждой операции;

в) к несовпадению числа операций и числа различных ресурсов;

г) к такому распределению (назначению) ресурсов, чтобы общая стоимость выполнения операций была минимальна или прибыль максимальна;

д) содержимое п.а, г.

17. Когда возникает задача массового обслуживания?

а) когда есть клиенты, пристраивающиеся к концу очереди;

б) когда есть клиенты, ожидающие в очереди момента;

в) когда есть клиенты, могущие пройти через средство обслуживания;

г) когда есть обслуженные клиенты, вышедшие из канала обслуживания (также указана скорость обслуживания);

д) содержание п. а-г.

18. В чем заключается “задача коммивояжера”?

а) выбрать некоторый маршрут, начинающийся в “родном” городе коммивояжера, проходящий через каждый из остальных городов только один раз и оканчивающийся в пункте отправления, который характеризуется минимальной длиной;

б) в выборе маршрута;

в) выбрать некоторые маршруты, начинающиеся в “родном” городе коммивояжера, проходящие через каждый из остальных городов несколько раз и оканчивающиеся в пункте отправления, которые характеризуются минимальной длиной;

г) выбрать некоторые маршруты;

д) выбор задач для такой широко распространенной фигуры, как коммивояжер, или агент по сбыту.

19. Для чего применяются методы исследования операций при многократных закупках оборудования?

а) для изучения вопроса о том, какое число запчастей следует хранить на складе и должны ли это быть отдельные части или собранные узлы;

б) для выбора типа и определения габаритов оборудования;

в) для определения сроков его замены и для принятия решений относительно того, чем именно его заменять;

г) для решения вопроса о целесообразности аренды или закупки оборудования и выяснения того, в каком случае использованное или модернизированное оборудование предпочтительнее нового;

д) для всего вышеперечисленного.

20. Какие вопросы охватывают исследование операций для распределения производственных заказов между предприятиями?

а) определение размера партий производимых изделий;

б) как определение технологий;

в) как определение последовательности операций и календарных графиков, состава и размещения запасов, выбора ассортимента продукции, которую можно производить из имеющегося сырья;

г) как определение целесообразности увеличения числа рабочих смен или применения сверхурочных работ;

д) все вышеназванные.

21. Для чего применяется исследование операций при сбыте продукции?

а) для определения пунктов размещения оптовых складов продукции, их емкости, количества и ассортимента запасов, хранимых на этих складах;

б) для определения круга потребителей, которым должна поставляться продукция с этих складов;

в) содержание п. а, б;

г) для стабилизации объема производства и уровня занятости, при определении затрат, обусловливаемых неустойчивостью, и влияния неустойчивости на общество;

д) для изучения вопроса о том, какое число запчастей следует хранить на складе и должны были это быть отдельные части или собранные узлы.

22. Для чего применяется исследование операций в научно-исследовательских и опытно-конструкторских работах?

а) для создания отчетов о работе;

б) для определения размеров ассигнований на научно-исследовательские разработки, распределения этих ассигнований между теоретическими и прикладными научными разработками и выбора отдельных программ, на которые целесообразно отпускать средства;

в) для определения того, какие силы (оборудование и персонал) должны выделяться для решения тех или иных задач и каковы оптимальные методы исследования этих сил;

г) для выбора областей, где целесообразно сосредоточить проведение научных и опытно-конструкторских работ, формирование критериев для оценки различных конструкций новых изделий, а также определение их надежности и сроков службы;

д) содержание п. б, в, г.

23. Чем отличаются методы исследования операций от методов других дисциплин?

а) объектом изучения;

б) методами самих исследований;

в) рассматриваемыми задачами;

г) набором симптомов;

д) инструментальными средствами.

24. Как найти оптимальное решение, если их число вариантов велико?

а) способом “простого перебора”;

б) методом “направленного перебора”;

в) содержание п. а, б;

г) логическими рассуждениями;

д) все вышеперечисленное.

25. Какие факторы, от которых зависит успех операции, Вы знаете?

а) заданные, заранее известные факторы (условия выполнения операции);

б) не зависящие от нас элементы решения, образующие в своей совокупности решение;

в) зависящие от нас элементы решения, образующие в своей совокупности решение;

г) содержание п. а, б;

д) содержание п. а, в;

26. Какой является задача о выборе решения при наличии неопределенных факторов?

а) детерминированной задачей;

б) задачей о выборе решения в условиях неопределенности;

в) нестохастической задачей;

г) задачей с нечетким множеством;

д) все вышеназванное.

27. Определите, к какому типу задач исследования операций относится следующий пример. Пусть организуется или реорганизуется работа столовой с целью повысить ее пропускную способность. Нам в точности неизвестно, какое количество посетителей придет в нее за рабочий день, когда именно они будут появляться, какие блюда заказывать и сколько времени будет продолжаться обслуживание каждого из них. Однако характеристики этих случайных величин, если сейчас еще не находятся в нашем распоряжении, могут быть получены статистическим путем.

а) детерминированной задачей;

б) задачей о выборе решения в условиях неопределенности;

в) стохастической задачей;

г) задачей с нечетким множеством;

д) все вышеназванное.

28. Определите, к какому типу задач исследования операций относится следующий пример:

Организуется система профилактического и аварийного ремонта технических устройств с целью уменьшить простои техники за счет неисправностей и ремонтов. Отказы техники, длительности ремонтов и профилактик носят случайный характер. Характеристики всех случайных факторов, входящих в задачу, могут быть получены, если собрать соответствующую статистику.

а) детерминированной задачей;

б) задачей о выборе решения в условиях неопределенности;

в) стохастической задачей;

г) задачей с нечетким множеством;

д) все вышеназванное.

29. В каких случаях неизвестные факторы не могут быть изучены и описаны статистическими методами?

а) распределение вероятностей для параметров в принципе существует, но к моменту принятия решения не может быть получено;

б) распределение вероятностей для параметров вообще не существует;

в) распределение вероятностей для параметров в принципе существует;

г) содержание п. а, б;

д) содержание п. а, в.

30. Какие задачи исследования операций принадлежат к сложным и трудным вычислительным задачам, при решении которых часто приходится прибегать к приближенным, так называемым “эвристическим” методам оптимизации?

а) задачи линейного программирования;

б) задачи целочисленного программирования;

в) задачи нелинейного программирования;

г) задачи стохастического программирования;

д) задачи п.п. б, в, г.

31. Если решение появляется в результате скрытой работы интеллекта человека, то оно называется:

а) формальным; б) стохастическим; в) творческим.

32. Неконтролируемые факторы, влияющие на критерий принятия решения, для каждого из которых известна только область, внутри которой находится закон распределения, называются:

а) стохастические; б) детерминированные; в) неопределённые.

33. Задачи принятия решения, где критерий оптимальности и ограничения не зависят от времени, называют:

а) динамические б) статические; в) функциональные.

34. Для ситуаций, в которых происходит выбор решений, характерны:

а)наличие цели; б)отсутствие ограничений; в)однокритериальность.

ГЛОССАРИЙ

Автономная модель – часть системы моделей, которую можно анализировать независимо от других частей. Этот подход применим всюду, где отдельные хозяйственные звенья обладают самостоятельностью в своих действиях. Однако в экономике все связано, поэтому автономность частичных моделей всегда относительна.

Авторегрессивная модель – статистическое описание связи значений одного и того же показателя в разные моменты времени.

Агрегирование – объединение, укрупнение показателей по какому-либо признаку. С математической точки зрения агрегирование рассматривается как преобразование модели в модель с меньшим числом переменных и ограничений (агрегированную модель), дающую приближенное (по сравнению с исходным) описание изучаемого процесса или объекта.

Адаптация – приспособление системы к реальным условиям. Различают адаптацию пассивную – реагирование системы на изменение среды и активную – воздействие системы на среду.

Адекватность модели – соответствие модели моделируемому объекту или процессу.

Агрегирование – преобразование модели в модель с меньшим числом переменных или ограничений – аг­регированную модель, дающую при­ближенное по сравнению с исход­ной описание изучаемого объекта.

Алгоритм – формализованная последовательность действий по решению задачи.

Алгоритм кратчайшего путипозволяет найти кратчайший путь в сети.

Алгоритм максимального пото­ка– позволяет определить путь с максимальной пропускной способ­ностью.

Аналитическая модель – формула, представляющая математические зависимости в экономике.

Антагонистические игры– игры, в которых интересы игроков строго противоположны, т. е. выигрыш одного игрока – проигрыш другого.

Аппроксимация – приближен­ное выражение математических объ­ектов через более простые объекты, например, сведение задачи выпук­лого программирования к кусочно-линейной задаче путем аппроксима­ции целевой функции и ограничений кусочно-линейными функциями.

Базисное решение – допусти­мое решение задачи линейного программирования, находящееся в вер­шине области допустимых решений.

Балансовая модель – 1. Система уравнений (балансовых уравнений), которые удовлетворяют требованию соответствия двух элементов: наличие ресурса и его использования. 2. При описании экономической системы в целом – система уравнений, каждое из которых выражает требование баланса между производимым отдельными экономическими объектами количеством продукции и совокупной потребность в этой продукции.

Бюджетное множество – множество наборов товаров (x₁, x₂, . . ., x_n), доступных индивиду при его доходе Q ценах (p₁, p₂, . . ., p_n).

Валовой выпуск – стоимость продуктов и услуг, являющихся результатом деятельности хозяйственных объектов страны в течение данного периода (года). Включает выпуск продуктов, рыночных и нерыночных услуг. При вычитании из валового выпуска промежуточного потребления получается валовой внутренний продукт – как конечный результат производственной деятельности.

Вальраса система уравнений – одна из первых экономико-математических моделей. В ней сформулирован процесс автоматического стремления рыночной экономики к стабильному равновесию в форме линейных уравнений, переменными в которых выступают количества товаров и ресурсов, а также цены на каждый из них, балансирующие спрос и предложение. Основное равенство (закон Вальраса) утверждает, что общая величина спроса должна быть при соответствующей системе цен равна общей величине предложения.

Вектор “затрат – выпуска” – вектор, содержащий компоненты двух видов: выпускаемые продукты (обычно положительные) и продукты, затрачиваемые в производстве (отрицательные).

Венгерский метод – метод ре­шения комбинаторных задач.

Вероятность – численная мера возможности события.

Взаимозаменяемость ресурсов – возможность альтернативного использования разных ресурсов: а) для сохранения или достижения заданного уровня производства, б) для достижения оптимума.

Геометрическая интерпретация задачи линейного программирования– интерпретация зависимостей, имеющих место в задаче линейного программирования в виде геометрических фигур (точек, прямых, полуплоскостей, многоугольников) в декартовой системе координат.

Гессе матрица – матрица вторых частных производных функций нескольких переменных. Характеристика матрицы Гессе (ее положительная или отрицательная определенность и полуопределенность) служит условием для определения вида стационарной точки: является ли она, соответственно, минимумом, максимумом или седловой точкой в задаче оптимизации функции.

Госсена законы – 1. Предельная полезность любого товара уменьшается по мере увеличения его потребления. 2. Индивиду невыгодно потреблять одно благо вместо другого и вообще как-то изменять структуру потребления, поскольку всякое такое изменение только ухудшает его благосостояние.

Градиент – вектор, направленный в сторону наискорейшего возрастания функции и равный по величине ее производной в этом направлении.

Граничные условия – предельно допустимые значения пере­менных.

Двойственные оценки опреде­ляют дефицитность используемых ресурсов и показывают, насколько возрастает максимальное значение целевой функции прямой задачи при увеличении количества соответствующего ресурса на еди­ницу.

Дерево – многоуровневая ие­рархическая система, в которой все вершины распределены по нескольким уровням.

Детерминированные величи­ны – исходные данные, заданные определенными величинами.

Динамические модели экономики – модели, описывающие экономику в развитии (в отличие от статических, характеризующих ее состояние в определенный момент).

Динамическое программирование – методы решения задач, в ко­торых процесс нахождения решения является многоэтапным.

Дисперсия характеризует раз­брос значений случайной величины.

Дисциплина очереди описыва­ет порядок обслуживания требова­ний в системе.

Допустимый план – решение, удовлетворяющее системе ограни­чений, но не обязательно опти­мальное.

Достоверное событие – собы­тие, которое непременно должно произойти.

Задача о диетезаключается в определении рациона, удовлетворяющего потребностям в питатель­ных веществах при минимальной стоимости.

Задача коммивояжера состоит в отыскании наилучшего маршрута для коммивояжера, который дол­жен объехать заданные города и вер­нуться назад за кратчайший срок или с наименьшими затратами.

Задача математического программирования.В общей постановке задачи этого раздела выглядят следующим образом. Имеются какие-то переменные и функция этих переменных f(x)=f(x₁,x₂,...,x_n), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции при условии, что переменные x принадлежат некоторой области G.

Задача о назначениях показы­вает, как распределить кандидатов по вакансиям наилучшим образом.

Задача о раскрое – как раскро­ить листы с минимальными затра­тами.

Задача о рюкзаке – задача о наилучшем использования ограни­ченного объема.

Задача оптимизации – задача, решение которой сводится к нахождению максимума или минимума целевой функции.

Золотое правило накопления– в условиях модели экономического роста фонд потребления на душу населения растет с максимальным темпом, если норма сбережения равна эластичности объема выпуска по капиталу.

Игра – формализованная мо­дель конфликтной ситуации.

Игра n лиц с постоянной суммой– игры, в которых принимает участие n игроков, существует n множеств стратегий и n действительных платежных функций от n переменных, каждая из которых является элементом соответствующего множества стратегий. Каждый игрок знает всю структуру игры и в своем поведении неизменно руководствуется желанием получить максимальный средний выигрыш.

Игра двух лиц с ненулевой суммой– игры, в которых сумма выирышей двух игроков после каждой партии не равна нулю.

Игра двух лиц с нулевой суммой– игры, в которых интересы двух игроков строго противоположны, т.е. выигрыш одного есть проигрыш другого.

Игра против природы– игры, где одним из определяющих факторов является внешняя среда или природа, которая может находиться в одном из состояний, которые неизвестны лицу, принимающему решение.

Игра с нулевой суммой– игры, в которых сумма выигрыша игроков после каждой партии составляет ноль.

Игрок – участник игровой мо­дели.

Изокванта – геометрическое место точек, в которых различные сочетания факторов производства дают одно и то же количество выпускаемой продукции.

Изоклиналь– линия наибольшего роста производственной функции. Изоклинали ортогональны изоквантам.

Имитационное моделирование – моделирование случайных величин.

Исследование операций– наука, занимающаяся разработкой и практическим применением методов оптимального управления организационными системами.

Итерация – этап реализации алгоритма, отличающийся от его других этапов (кроме начального и конечного) лишь значениями пере­менных величин, но не составом процедур обработки информации.

Канал обслуживания – устрой­ство для обслуживания требований в очереди.

Кейнсианская теория экономики – модели, описывающие экономику в развитии с использованием математических методов.

Коалиции игроков– объединение m игроков в игре n лиц (m меньше n) с целью получения максимального выигрыша и выработке соответствующих стратегий.

Кобба – Дугласа функция – производственная функция, примененная американскими исследователями Ч. Коббом и П. Дугласом при анализе развития экономики США в 20-30 гг. нашего века. Имеет следующую форму 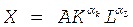, где X – национальный доход, A – коэффициент размерности, K , L – соответственно бъемы приложения капитала и труда, 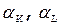– константы, коэффициенты эластичности по капиталу и по труду.

Конечный узел, сток – конечная вершина сети или состояние, которым завершается комплекс работ.

Коэффициенты линейных ог­раничений – нормы расхода ре­сурсов.

Коэффициенты прямых затрат – (технологические коэффициенты) в межотраслевом балансе – средние величины непосредственных затрат продукции одной отрасли (в качестве средств производства) на выпуск единицы продукции другой отрасли. Они могут быть выражены в натуральной форме и в ценностной.

Коэффициенты эластичности производства – показатели производственной функции, характеризующие относительное изменение результатов на единицу относительного изменения затрат i-го ресурса.

Кривая безразличия – геометрическое место точек пространства товаров, характеризующихся состоянием безразличия с точки зрения потребителя или производителя.

Критический путь – путь в сети наибольшей продолжительности.

Линейное программирование – методы решения задач математического программирования, в которых ограничения и целевая функция линейны.

Линейно-независимые уравне­ния – уравнения, которые не мо­гут быть получены умножением, делением, сложением, вычитанием исходных уравнений.

Линейные зависимости – зави­симости, в которые переменные входят в первой степени, и в кото­рых нет их произведения.

Линия уровня – линией уровня на поверхности Y= F(K,L) называется множество тех точек поверхности, для которых F(K,L)=const.

Магистраль – основное понятие математической теории равномерного пропорционального роста экономики, основы которой были заложены американским математиком Дж. Фон Нейманом. Это траектория (путь) развития, при которой теоретически, за длительное время, достигается максимальная скорость роста экономики.

Макроэкономическая модель – экономико-математическая модель, отражающая функционирование народного хозяйства как единого целого. Макромодели оперируют, как правило, стоимостными показателями – национальный доход, валовые капиталовложения и другие. Важным приложением является прогнозирование народнохозяйственных процессов. Для этого используются макроэкономические производственные функции.

Математическое ожидание ха­рактеризует среднее значение случайной величины.

Межотраслевой баланс отража­ет производство и распределение валового национального продукта в отраслевом разрезе, межотрасле­вые производственные связи, ис­пользование материальных и тру­довых ресурсов, создание и распределение национального дохода.

Межпродуктовый баланс исполь­зуется для обеспечения полной взаимоувязки планов производства группы взаимосвязанных предпри­ятий либо группы цехов одного предприятия.

Метод ветвей и границ – метод решения задачи о назначениях.

Метод критического пути – ме­тод решения сетевых задач, в ко­торых продолжительности работ – детерминированные величины.

Метод Монте-Карло – метод решения задач моделированием слу­чайных величин (метод статисти­ческих испытаний).

Метод потенциалов — метод ре­шения транспортной задачи.

Метод рекуррентных соотно­шений Беллмана – основной ме­тод динамического программиро­вания, в основе которого лежит следующий принцип оптималь­ности: если управление процесса оптимально, то оно будет опти­мальным и для процесса, остаю­щегося после осуществления очередного шага.

Метод северо-западного угла – метод решения транспортной за­дачи.

Микроэкономическая м<