РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Обыкновенное дифференциальное уравнение (ОДУ) порядка p относительно неизвестной функции y одного независимого переменного x записывается как

.

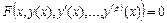Мы будем рассматривать уравнения первого порядка вида

y′ = f(x,y) (6.1)

или системы уравнений первого порядка, например:

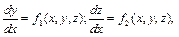(6.2)

где y = y(x), z = z(x).

Отметим, что уравнения высших порядков можно свести к системе уравнений первого порядка. Например, уравнение второго порядка 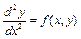заменой 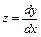сводится к системе из двух дифференциальных уравнений:

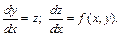
Из теории дифференциальных уравнений известно, что общее решение уравнения (6.1) содержит одну произвольную константу: y = y(x) + C, т.е. определяет семейство кривых, а общее решение (6.2) содержит две произвольные константы и имеет вид y = y(x) + C₁; z = z(x) + C₂.

Для однозначного нахождения решения уравнения (6.1) или системы (6.2) необходимо задать дополнительные условия. Если эти дополнительные условия задаются в одной точке интервала [a, b], например, y(a)=y_a для уравнения (6.1) или y(a)=y_a; z(a)=z_a для системы (6.2), то это задача Коши, если в нескольких (например, y(a)=y_a; z(b)=z_b для системы (6.2)), то это краевая задача.

Задачи для дифференциальных уравнений (Коши, краевые) делятся на два класса: линейные и нелинейные.

Линейная задача определяется линейными дифференциальными уравнениями и линейными дополнительными условиями.

Постановка нелинейной задачи содержит либо нелинейное дифференциальное уравнение, либо нелинейное условие, либо то и другое.

Методы решения ОДУ можно условно разбить на точные, приближенные и численные.

Точные методы рассматриваются в курсе дифференциальных уравнений.

Приближенные методы используют различные упрощения самих уравнений, специальный выбор класса искомых функций, разложение решения в ряд по малому параметру, асимптотические методы.

Нисколько не умаляя значения этих классических методов решения дифференциальных уравнений, следует отметить, что очень часто в практических задачах такие методы или вообще неприменимы, или приводят к таким сложным решениям, что затраты труда на их получение превосходят все разумные пределы.

Поэтому (и в связи с появлением быстродействующих ЭВМ) широкое распространение получили численные методы, в основе которых лежит замена исходного уравнения его дискретным аналогом – разностным уравнением.

При этом область непрерывного изменения аргумента заменяется дискретным множеством точек (узлами): x®x_k. Узлы составляют разностную сетку.

Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке: y®y_k. Эта функция называется сеточной функцией. Она определена только в узлах разностной сетки.

Исходное дифференциальное уравнение приближенно заменяется разностным уравнением относительно сеточной функции: Ly=f(x,y)®L_ky_k=f(x_k,y_k), где L – дифференциальный оператор, L_k – разностный оператор. При этом производные заменяются по известным нам формулам численного дифференцирования. Такая замена дифференциального уравнения на разностное называется аппроксимацией. Граничные условия также заменяются их разностными аналогами.

Совокупность разностных уравнений, аппроксимирующих исходное дифференциальное уравнение или систему дифференциальных уравнений и дополнительные условия на границах, называется разностной схемой.

Решение разностной задачи, в результате которого находятся значения сеточной функции y_k в узлах x_k , приближенно заменяет решение y(x) исходной дифференциальной задачи. Однако не всякая разностная схема дает удовлетворительное решение (например, с точки зрения точности). К разностной схеме предъявляются определенные требования, касающиеся устойчивости, аппроксимации и сходимости разностной схемы. Об этих понятиях упоминалось во введении.

Разностная схема называется устойчивой, если на каждом шаге счета любая ошибка (погрешность аппроксимации, погрешность округления и т.п.) не возрастает при переходе от одного шага к другому.

Если решение существует, единственно и если схема устойчива, то разностная схема называется корректной.

Разностное уравнение аппроксимирует дифференциальное уравнение, если погрешность аппроксимации стремится к нулю при измельчении сетки. Погрешность аппроксимации – это разность между дифференциальным уравнением и его разностным аналогом.

Пусть d_k – разница между значениями сеточной функции и искомой функции в узле сетки x_k, т.е. d_k = y_k(x_k) – y(x_k).

Тогда y_k(x_k) = y(x_k) + d_k .

Подставляем в разностное уравнение:

L_ky(x_k) + L_kd_k = f_k (x_k, y_k),

Здесь L_kd_k = R_k – погрешность аппроксимации.

Если R_k = O(h^p), то разностная схема имеет p-тый порядок аппроксимации.

Если 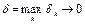при h®0, то говорят, что разностная схема сходится (т.е. решение разностной задачи сходится к решению дифференциальной задачи). Сходимость считается одним из важных критериев качества разностной схемы. Сходимость трудно установить прямым путем. Для некоторого класса линейных задач справедливо утверждение (теорема Лакса):

если имеется корректно поставленная линейная задача с начальными условиями и конечно разностное уравнение аппроксимирует исходное дифференциальное уравнение, то устойчивость является необходимым и достаточным условием сходимости,

или кратко:

аппроксимация + устойчивость = сходимость.

Для нелинейных же задач эта теорема не всегда строго применима, так что в этом случае правильнее говорить только о необходимых условиях сходимости.

Многолетняя практика использования численных методов для решения практических задач на ЭВМ показывает, что применение той или иной разностной схемы, даже если она исследована теоретически, требует её тщательной апробации при решении конкретной задачи. Для этого проводятся методические вычислительные эксперименты (расчеты с разными шагами при разных исходных данных), или проводятся расчеты тестовых задач, для которых либо найдено аналитическое решение, либо имеется численное решение, полученное другим численным методом.