Решение уравнений 4 степени
Рассмотрим способ решения, предложенный Феррари, одним из учеников Кардано.
Уравнение
x4+ax3+bx2+cx+d=0, (1)
где a,b,c,dÎC, будем называть уравнением 4-ой степени общего вида. Выполним некоторые преобразования:
x4+ax3+bx2+cx+d=0Ûx4+ax3=-bx2-cx-d. (2)
К обеим частям уравнения прибавим 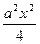 , получим
, получим
x4+ 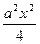 +ax3=-bx2 +
+ax3=-bx2 + 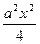 -cx-d Û (x2+
-cx-d Û (x2+ 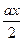 )2=(
)2=( 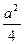 -b) x2-cx-d. (3)
-b) x2-cx-d. (3)
Введем вспомогательную переменную, для этого к обеим частям прибавим
(x2+ 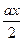 )y+
)y+ 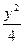 , получим
, получим
(x2+ 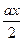 )2+(x2+
)2+(x2+ 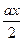 )y+
)y+ 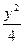 =(
=( 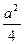 -b) x2-cx-d+(x2+
-b) x2-cx-d+(x2+ 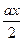 )y+
)y+ 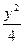 Û
Û
Û(x2+ 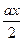 +
+ 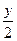 )2=(
)2=( 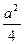 -b+y) x2+(
-b+y) x2+( 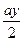 -c)x+(
-c)x+( 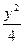 -d). (4)
-d). (4)
Теперь подбираем y так, чтобы в левой части равенства получить полный квадрат, для этого решим систему четырех уравнений с четырьмя неизвестными
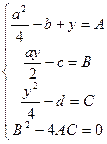 . (5)
. (5)
Решив эту систему уравнений, найдем значение y. При решении системы получается уравнение третьей степени, которое можно решать по формулам Кардано.
Замечание. Так как нам достаточно найти одно значение y, то иногда удобнее решать уравнение другими методами, в частности подбором.
Пусть y0 – одно из найденных значений переменной y, тогда уравнение (4) примет вид
(x2+ 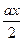 +
+ 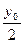 )2=(ax+b)2, а это равносильно совокупности двух квадратных уравнений
)2=(ax+b)2, а это равносильно совокупности двух квадратных уравнений
x2+ 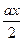 +
+ 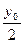 =ax+b или
=ax+b или
x2+ 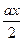 +
+ 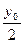 =-ax-b. (6)
=-ax-b. (6)
Решив уравнения (6), получим четыре корня уравнения (1).
Пример. Решить уравнение x4+2x3+5x2+6x+9=0 Û x4+2x3=-5x2-6x-9Û
x4+2x3 +x2=-5x2-6x-9+ x2Û( x2+x)2=-4x2-6x-9. Введем вспомогательную переменную, получим
( x2+x)2 +( x2+x)y + 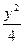 =-4x2-6x-9+( x2+x)y +
=-4x2-6x-9+( x2+x)y + 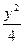 Û
Û
( x2+x+ 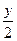 )2=(y-4) x2-(y-6)x+(
)2=(y-4) x2-(y-6)x+( 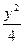 -9).
-9).
Составим и решим систему уравнений
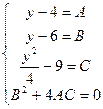 .
.
B2-4AC=(y-6)2-4(y-4) ( 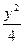 -9)=y2-12y+36-y3+36y+4y2-144=0Û
-9)=y2-12y+36-y3+36y+4y2-144=0Û
-y3 +5y2+24y-108=0 Û (y-6)(-y2-3y+18)=0, y1=6, получим
( x2+x+3)2=2 x2 Û x2+x+3= 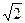 х Ú x2+x+3=-
х Ú x2+x+3=- 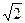 хÛ
хÛ
x2+(1- 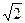 )х+3=0 Ú x2+ (1+
)х+3=0 Ú x2+ (1+ 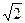 )х+3=0,
)х+3=0,
x1,2= 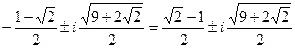 ,
,
x3,4= 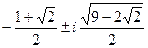 .
.
Замечание. Недостаток формулы Кардано состоит в том, что она часто представляет рациональные корни в иррациональном виде. Например, легко видеть, что число 2 является корнем уравнения x3-x-6=0, а формула Кардано дает y= 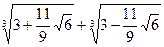 . Других действительных корней данное уравнение не имеет, так как его дискриминант положителен, а это выражение дает только приближенное значение корня. Из-за этого недостатка рекомендуется рациональные корни кубического уравнения с целыми коэффициентами искать не по формулам Кардано, а другими способами, о которых будем говорить позднее.
. Других действительных корней данное уравнение не имеет, так как его дискриминант положителен, а это выражение дает только приближенное значение корня. Из-за этого недостатка рекомендуется рациональные корни кубического уравнения с целыми коэффициентами искать не по формулам Кардано, а другими способами, о которых будем говорить позднее.
СПИСОК ЛИТЕРАТУРЫ.
1. Каргополов М.И., Мерзляков Ю.И. Основы теории групп. М.: Наука, 1982.
2. Кострикин А.И. Введение в алгебру. М.: Наука, 1977.
3. Курош А.Г. Теория групп. М.: Наука, 1977.
4. Ляпин Е.С., Айзенштат А.Я., Лесохин М.М. Упражнения по теории групп. М., 1967.
5. Фаддеев Д.К. Лекции по алгебре. М.: Наука, 1984.
6. Холл М. Теория групп. М. 1962.
7. Курош А.Г. Лекции по общей алгебре. М., 1962.
8. Мендельсон Э. Введение в математическую логику. М.: Наука, 1984
9. Лесохин М.М., Лукъяненков К.Ф., Пиотровский Р.Г. Введение в математическую лингвистику. Минск: Наука и техника.
Дата добавления: 2020-10-25; просмотров: 206;










