Корни n-ой степени из единицы
Так как 1ÎС и 1¹0, то по только что доказанному существует ровно n значений корня n-ой степени из 1. Поскольку 1=1+0i=cos0+isin0, тогда 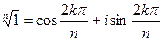 , где k=0, 1, 2, …, n-1
, где k=0, 1, 2, …, n-1
Обозначим все множество корней n-ой степени из 1 через En={e0,e1,e2,…,en-1}, где em=cos 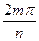 +isin
+isin 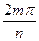 .
.
Теорема. Множество корней n-ой степени из 1 образует группу относительно операции умножения.
Доказательство
Так как EnÌС и 0Ï En, то En является подмножеством мультипликативной группы поля С, и можно воспользоваться теоремой о подгруппе. Проверим выполнимость двух условий:
1) "ek,emÎEn(ekemÎEn);
2) "ekÎEn(ek-1ÎEn).
Пусть ek,emÎEn Û ek=cos 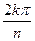 +isin
+isin 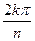 , em=cos
, em=cos 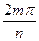 +isin
+isin 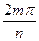 , где 0£k£n-1, 0£m£n-1, тогда
, где 0£k£n-1, 0£m£n-1, тогда
ekem=(cos 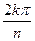 +isin
+isin 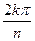 )(cos
)(cos 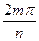 +isin
+isin 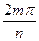 )=cos(
)=cos( 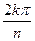 +
+ 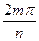 )+isin(
)+isin( 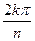 +
+ 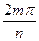 )=cos
)=cos 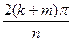 + isin
+ isin 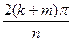 . По теореме о делении с остатком в кольце целых чисел, мы можем записать k+m=nq+r, где 0£r£n-1, тогда
. По теореме о делении с остатком в кольце целых чисел, мы можем записать k+m=nq+r, где 0£r£n-1, тогда
ekem= cos 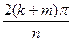 + isin
+ isin 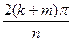 =cos
=cos 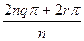 +isin
+isin 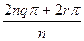 =
=
=cos(2qπ+ 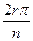 )+isin(2qπ+
)+isin(2qπ+ 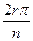 )= cos
)= cos 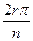 +isin
+isin 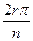 ÎEn, так как 0£r£n-1. Первое условие теоремы о подгруппе выполняется.
ÎEn, так как 0£r£n-1. Первое условие теоремы о подгруппе выполняется.
Единица 1=e0=cos0+isin0ÎEn. Пусть ekÎEn Û ek=cos 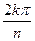 +isin
+isin 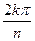 , где 0<k£n-1Þ 1-n£-k<0Þ 1£n-k<nÞ 0<n-k£n-1Þen-kÎEn. Самостоятельно доказать, что en-k=ek-1. Оба условия теоремы о подгруппе выполнены, следовательно, En – подгруппа мультипликативной группы комплексных чисел, и теорема доказана.
, где 0<k£n-1Þ 1-n£-k<0Þ 1£n-k<nÞ 0<n-k£n-1Þen-kÎEn. Самостоятельно доказать, что en-k=ek-1. Оба условия теоремы о подгруппе выполнены, следовательно, En – подгруппа мультипликативной группы комплексных чисел, и теорема доказана.
Теорема. Все корни n-ой степени из произвольного комплексного числа можно получить, умножив один из них на все корни n-ой степени из 1.
Доказательство.
Пусть aÎС, 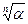 Î{b0,b1,…,bn-1},
Î{b0,b1,…,bn-1}, 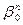 =aÙ"k (
=aÙ"k ( 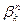 =a), следовательно,
=a), следовательно,
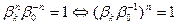 , а это означает, что
, а это означает, что 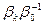 =e - корень n-ой степени из единицы, тогда bk=b0e. Так как k было взято произвольно, то полученный результат справедлив для любого bk. Обратно, если b0 – корень n-ой степени из a, e- корень n-ой степени из единицы и b=b0e, тогда
=e - корень n-ой степени из единицы, тогда bk=b0e. Так как k было взято произвольно, то полученный результат справедлив для любого bk. Обратно, если b0 – корень n-ой степени из a, e- корень n-ой степени из единицы и b=b0e, тогда
bn =(b0e)n=b0nen=a1=a.
Замечание. Эта теорема показывает, что корни n-ой степени из единицы при извлечении корня играют ту же роль, что знаки ± при извлечении квадратного корня.
Примеры
1) 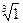 =соs
=соs 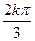 +isin
+isin 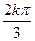 , где k=0, 1, 2
, где k=0, 1, 2
e0=cos0+isin0=1,
e1=cos 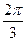 +isin
+isin 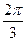 =cos(π-
=cos(π- 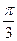 )+isin(π-
)+isin(π- 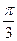 )=-cos
)=-cos 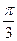 +isin
+isin 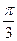 =-
=- 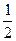 +i
+i 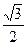 ,
,
e2=cos 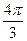 +isin
+isin 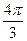 =cos(π+
=cos(π+ 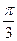 )+isin(π+
)+isin(π+ 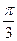 )=-cos
)=-cos 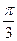 -isin
-isin 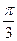 =-
=- 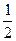 -i
-i 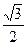 ;
;
2) 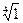 =соs
=соs 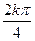 +isin
+isin 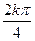 = соs
= соs 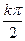 +isin
+isin 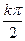 , где k=0, 1, 2, 3
, где k=0, 1, 2, 3
e0=cos0+isin0=1,
e1= соs 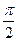 +isin
+isin 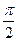 =0+i=i,
=0+i=i,
e2= соs 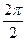 +isin
+isin 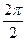 =cos π+isin π=-1,
=cos π+isin π=-1,
e3= соs 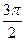 +isin
+isin 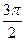 =0-i=-i.
=0-i=-i.
Геометрическое представление корней n-ой степени из единицы
Мы уже рассматривали геометрический смысл корней n-ой степени из произвольного комплексного числа. На основании всех известных нам результатов можно сделать вывод, что все корни n-ой степени из 1 лежат на окружности единичного радиуса с центром в начале координат и делят эту окружность на n равных частей, начиная от оси ОХ.
Первообразные корни n-ой степени из единицы
Пусть nÎN и e некоторый корень n-ой степени из единицы. Будем называть этот корень первообразным корнем n-ой степени из единицы, если en=1, а ek¹1 "k<n.
Замечание. Очевидно, что 1 входит в число корней любой степени из единицы, но она не является первообразным корнем никакой степени n³2 из единицы.
Примеры
1) n = 2 , √1=±1
-1 – первообразный корень 2 степени из 1, так как (-1)1¹1, (-1)2=1;
2) n=3, 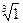 Î{1, -
Î{1, - 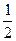 +i
+i 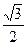 , -
, - 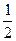 -i
-i 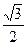 }
}
e1=- 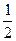 +i
+i 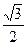 - первообразный корень 3 степени из единицы, действительно, e11¹1, e12=-
- первообразный корень 3 степени из единицы, действительно, e11¹1, e12=- 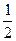 -i
-i 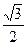 ¹1, e13=1.
¹1, e13=1.
Аналогично показать самостоятельно, что e2=- 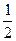 -i
-i 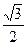 - первообразный корень 3 степени из единицы.
- первообразный корень 3 степени из единицы.
3) n=4, 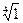 Î{1, -1, i, -i}
Î{1, -1, i, -i}
Очевидно, что -1 не является первообразным корнем 4 степени из единицы, так как (-1)2=1
i1=i ; i2=-1; i3=-i; i4=1; (-i)1=-i; (-i)2=-1; (-i)3=i; (-i)4=1, следовательно, ± i - первообразные корни 4 степени из единицы.
Теорема. Существуют первообразные корни любой степени n³2 из единицы.
Доказательство. Самостоятельно.
Указание! Методом от противного можно доказать, что e1 будет первообразным корнем любой степени n³2 из единицы.
Теорема. Пусть e - первообразный корень n-ой степени из единицы, тогда все элементы множества Е={e0, e1, e2,…, en-1} различны.
Доказательство
Предположим противное, пусть ek=em, где n>k>m³0. Разделив обе части равенства на em, получим ek-m=1, где n>k-m>0, что противоречит определению первообразного корня. Теорема доказана.
Следствие 1. Множество корней n-ой степени из единицы исчерпывается числами множества Е.
Доказательство. Так как все элементы множества Е различны и их число совпадает с числом корней n-ой степени из единицы, то достаточно показать, что любой элемент множества Е будет корнем n-ой степени из единицы. Пусть ekÎЕ, тогда (ek)n=(e n) k=1 k=1, что и требовалось доказать.
Следствие 2. Все корни n-ой степени из произвольного комплексного числа могут быть получены умножением одного из них на все степени первообразного корня той же степени из единицы.
Доказательство самостоятельно.
Дата добавления: 2020-10-25; просмотров: 1387;










