Метод простой итерации

В этом методе матрица С выбирается единичной: СºЕ. Тогда

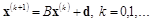
В координатной форме:

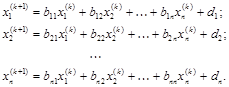
Для сходимости метода простой итерации достаточно , чтобы

||B||<1. (4.13)

Доказательство можно найти, например, в книге Ю.П. Боглаева [9].

Условие сходимости в разных нормах будет выглядеть следующим образом:

в евклидовой норме ;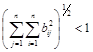

в норме Чебышева .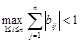

Гарантией сходимости итерационного процесса может служить выполнение хотя бы одного из достаточных условий в разных нормах.

Отсюда вывод: преобразование исходной системы Ах=b к итерационному виду x^(k+1)=Bx^(k)+d нужно осуществить таким образом, чтобы коэффициенты при неизвестных в правых частях стали существенно меньше единицы.

Отметим, что существует необходимое и достаточное условие сходимости метода простой итерации, формулируемое следующей теоремой.

Если Ах=b имеет единственное решение, то последовательные приближения x^(k+1)=Bx^(k)+d сходятся к решению исходной системы при любом начальном приближении х⁽⁰⁾ тогда и только тогда, когда все собственные значения матрицы В по модулю меньше единицы.

Однако этой теоремой непросто воспользоваться, так как требуется знание границ собственных значений матрицы В, что является самостоятельной достаточно сложной задачей (см. п. 4.7).

Можно указать некоторые приемы преобразования исходной системы уравнений к итерационной системе.

Например, получение системы с диагональным доминированием, то есть такой системы, у которой абсолютные величины диагональных коэффициентов больше суммы абсолютных величин недиагональных элементов этой строки (см. п. 4.4). Если теперь разделить все уравнения на соответствующие диагональные элементы и выразить из каждого уравнения неизвестное с коэффициентом, равным единице, то будет получена система с коэффициентами |b_ij|<1. Затем необходимо проверить условие сходимости. Если оно не выполняется ни в одной норме, то нужно вернуться к исходной системе и попытаться выполнить преобразование так, чтобы добиться лучшего результата[1].

Пример 3. Решить систему уравнений.

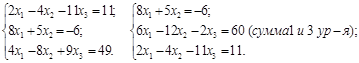
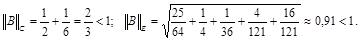Следовательно, итерационный процесс сходится – как в чебышевской, так и в евклидовой норме.

Используя достаточное условие сходимости, можно получить апостериорную оценку точности метода простой итерации.

Запишем исходное уравнение метода простой итерации и его итерационную схему:

,

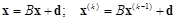или, вычитая,

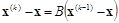. (4.14)

Нормируя получившееся выражение, имеем

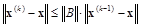. (4.15)

Преобразуем разность (4.14), прибавив к левой и правой части x^(k–1):

,

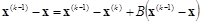или, нормируя и преобразовывая

,

.

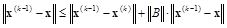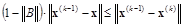Используя (4.15) и то, что (1–||B||)>0, окончательно получаем оценку

.

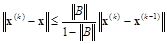Таким образом, для остановки итерационного процесса при заданной погрешности e можно использовать оценку

,

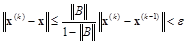или 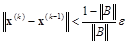. (4.16)

Если ||B||»0,5, то тогда можно использовать оценку .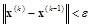

Существует и априорная оценка точности метода, с помощью которой можно определить необходимое число итераций для достижения заданной погрешности e [5].

.

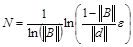Однако эта погрешность фактически оказывается весьма завышенной, поэтому малоупотребительна.

Метод Зейделя

Отличие метода Зейделя от метода простой итерации состоит лишь в том, что при вычислении (k+1)-ого приближения ранее полученные приближения сразу же используются в вычислениях. В координатной форме итерационный процесс Зейделя имеет вид:

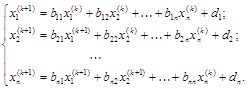(4.17)

Достаточное условие сходимости метода Зейделя можно получить, записав матричную форму итерационного процесса:

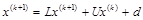
и проведя некоторые преобразования:

Рассматривая последнее выражение как запись итерационной схемы метода простой итерации для системы уравнений 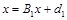, можно записать достаточное условие сходимости метода Зейделя в виде

, или .

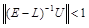Здесь –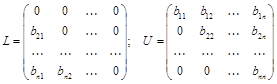

нижняя и верхняя треугольные части матрицы В, соответственно,

В формулах априорной и апостериорной оценки точности этого метода B заменяется на B₁.

Сразу виден недостаток этого способа оценки – его громоздкость (необходимо искать вспомогательные матрицы, обратную матрицу, проводить перемножение матриц – и все это для получения только достаточного условия сходимости).

Укажем один практический прием преобразования исходной системы Ах=bв систему вида x=Bx+d с гарантией сходимости итерационного процесса метода Зейделя.

Умножим левую и правую части исходной системы на транспонированную матрицу А^Т. Получим систему вида Сx=d, где C=A^TA; d=A^Tb. Эта система называется нормальной.

Ее свойства:

1) матрица С является симметрической (с_ij = c_ji);

2) все элементы главной диагонали матрицы С положительны: с_ii >0.

После этого проведем уже знакомое нам преобразование: делим каждое уравнение нормальной системы на соответствующий диагональный элемент.

Получаем так называемую приведенную систему

, где ,

и уже для приведенной системы записываем итерационный процесс Зейделя

.

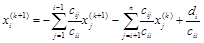x⁽⁰⁾ = d

Целесообразность осуществления описанных преобразований вытекает из того, что имеет место теорема:

Итерационный процесс Зейделя для приведенной системы, эквивалентной нормальной системе, всегда сходится к единственному решению этой системы при любом выборе начального приближения [1].

Пример 4.

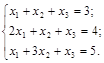
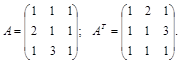
Тогда

,

.

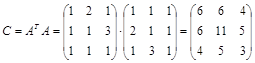Нормальная система: Приведенная система:

.

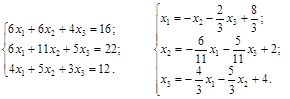Итерационная схема Зейделя:

.

Метод релаксации

Преобразуем исходную систему уравнений следующим образом: перенесем свободные члены в левую часть и разделим первое уравнение на – а₁₁, второе – на – а₂₂ и так далее, то есть на диагональные элементы, взятые с противоположными знаками.

Получим систему, приготовленную к релаксации:

.

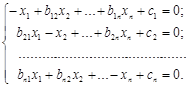Здесь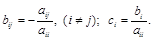

Выберем начальное приближение к решению – вектор 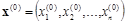и подставим его в преобразованную систему. Естественно, левые части будут отличаться от нуля. Вычислим так называемые невязки:

.

Замечаем, что если одной из неизвестных 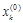дать приращение 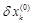, то соответствующая невязка 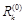уменьшится на величину 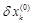, а все остальные невязки 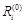(i ¹ k) увеличатся на величину 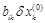. Таким образом, чтобы обратить очередную невязку 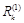в нуль, достаточно величине 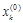дать приращение 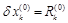и тогда будем иметь 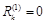. Остальные невязки (при i ¹ k ) получат значения .

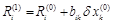Метод релаксации (или ослабления) заключается в том, что на каждом шаге обращают в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки последней преобразованной системы будут равны нулю с заданной точностью.

Пример 5.

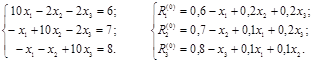
Задаем 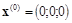. Тогда . Максимальная невязка равна 0,8. Тогда, согласно методу релаксации, полагаем 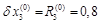и получаем первые невязки:

.

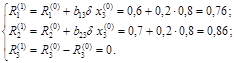Максимальная невязка равна 0,86. Полагаем 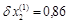и получаем вторые невязки и так далее. Значение корней получаются суммированием всех приращений 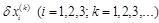. В рассматриваемом примере решение точное и сложится из следующих поправок:

х₁ = 0+0,93+0,07=1,0;

x₂ = 0+0,86+0,13+ 0,01=1,0;

x₃ = 0,80+0,18+0,02 = 1,0.