ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ И ОБРАТНОЙ

МАТРИЦЫ

Представим матрицу А в виде LU-разложения. Тогда

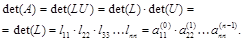
Таким образом, определитель матрицы можно найти как произведение диагональных элементов нижней треугольной матрицы в LU-разложении или как произведение ведущих элементов в схеме Гаусса. Следует только иметь в виду: если в процессе реализации схемы Гаусса производились перестановки строк или столбцов, то при нечетном числе перестановок det(A) = – det(L).

Пусть А^–1 ={a _ij }– матрица, обратная матрице А = {a _ij }, то есть А×А^–1 = 1, или ,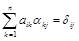

где 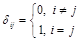i,j = 1… n. (4.7)

Пусть j = 1. Тогда a_i1 и d_i1 – векторы-столбцы и вид уравнения (4.7) ничем не отличается от координатного вида (4.1) уравнения Ах=b.

Следовательно, если мы каким-либо способом решим уравнение

,

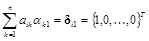то найдем первый вектор-столбец обратной матрицы {a_i1}.

Аналогично, полагая j = 2 и решая уравнение

,

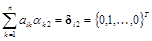получим второй столбец обратной матрицы {a _i2}.

Вывод: чтобы получить n столбцов обратной матрицы, необходимо n раз решить систему уравнений (4.7) с постоянной матрицей А и переменной правой частью, представляющей собой столбец с последовательно сдвигаемой единичкой. В этом поможет схема Халецкого.

Посмотрим на эту процедуру с точки зрения LU-разложения.

Этап 1. Находим элементы матриц L и U.

Этап 2. Решаем систему уравнений .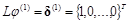

Этап 3. Решаем систему уравнений 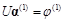и находим первый столбец обратной матрицы.

Этап 4. Повторяем этапы 2 и 3 n раз, сдвигая единицу в правой части.

Отметим, что, зная обратную матрицу, легко получить решение СЛАУ в виде .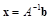

МЕТОД ПРОГОНКИ

Рассмотренные методы решения линейных систем уравнений, ориентированные на матрицы самого общего вида, оказываются крайне неэффективными, если использовать их для решения систем с трехдиагональными матрицами. Большую часть времени компьютер занимается обработкой нулевых элементов.

Трехдиагональные матрицы уже нам встречались – когда рассматривали задачу поиска коэффициентов кубического сплайна. Также они появляются при решении различных задач математической физики, например, при записи разностных уравнений линейных краевых задач (см. гл. 6).

Для решения систем с трехдиагональными матрицами используется вариант исключения Гаусса, в котором принимают участие лишь ненулевые элементы матрицы А. Это метод прогонки.

Пусть дана система линейных алгебраических уравнений вида

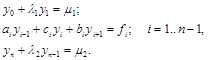(4.8)

Это обычный вид таких систем, которые появляются при решении практических задач. Здесь l , m , a, b, c – константы.

Запишем ее в развернутом виде.

.

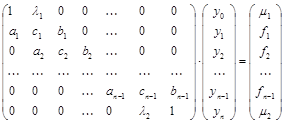Будем искать решение этой системы в виде рекуррентной формулы, связывающей y_i и y_i+1 :

, (4.9)

где a₁ и b₁ – известные константы (a₁º -l₁; b₁º m₁), а a₂, …, a_n и b₂,…, b_n – пока неизвестные константы.

Понизим в (4.9) индекс на 1:

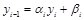. (4.10)

Теперь, подставляя (4.10) во второе уравнение системы (4.8):

,

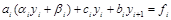где i=1, …, n–1, приходим к уравнению вида

.

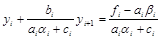Сравнивая полученное равенство с (4.9), находим

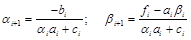. (4.11)

Эти рекуррентные соотношения называются формулами прямой прогонки. Они позволяют по заданным значениям a₁ и b₁ последовательно определить все пары прогоночных коэффициентов (a₂,b₂), (a₃,b₃),…, (a_n,b_n).

Затем начинается второй этап метода прогонки – обратная прогонка.

Запишем уравнение (4.9) для i=n–1 и добавим еще не использованное третье уравнение системы (4.8). Получаем систему из двух уравнений с двумя неизвестными y_n и y_n–1:

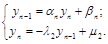
Ее решение: 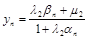. (4.12)

Все остальные значения y_i (i = n–1, n–2,…,0) находим по рекуррентной формуле (4.9). Формулы (4.12) и (4.9) называются формулами обратной прогонки.

Всегда ли работает этот метод? Ответ на этот вопрос дает теорема о достаточных условиях работы метода прогонки [7].

Теорема. Прогонка осуществима и устойчива, если выполнены неравенства a_i¹0; b_i¹0; ½c_i½³½a_i½+½b_i½, i=1, 2,…, n–1; ½l₁½£1; ½l₂½£1(условия диагонального доминирования), причем одно из последних неравенств – строгое.

Отметим, что для осуществимости прогонки необходимо показать, что из этих условий вытекает неравенство нулю знаменателей в формулах прогонки, а для устойчивости – что ½a_i+1½£1. В этом случае в формуле (4.9) ошибки, возникающие в ходе вычислений, не накапливаются, то есть не зависят от i.

Доказательство. Для i=1 ½a₁½=½l₁½£1. Пусть ½a_i½£1. Докажем, что .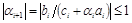

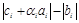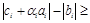
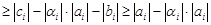
Рассмотрим разность . Так как 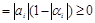, то

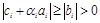. Откуда следует, что 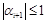и знаменатель в формулах прямой прогонки (4.11) в нуль не обращается.

Далее, пусть 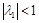, , 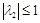тогда 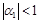, а значит, 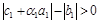, т.е. 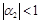. Проводя подобные рассуждения далее, получим, что 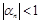, тогда 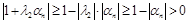. Теперь, пусть 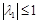, , 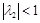тогда 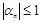и 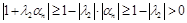. В обоих случаях знаменатель в формуле (4.12) не обращается в нуль.