Простейшие свойства кольца

Для любых элементов а, b, с кольца К=(К,+,×) имеет место:

1) если a+b=a, то b=0;

2) если a+b=0, то b=-a;

3) -(-а)=а;

4) 0×а=а×0=0;

5) (-а). b =а.(- b)=-(а b);

6) (-а)(-b)=аb;

7) (а- b)×с=а×с- b×с и с×(а- b)=с×а - с× b;

8) (a₁+a₂+…+a_n)(b₁+b₂+…+b_m)= ;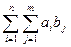

9) если К – коммутативное кольцо, тогда

"a,bÎK"nÎN((a+b)ⁿ= 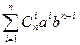, где .

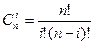Доказательство

1. Если a+b=a, то b=0+b=(-a+a)+b=-a+(a+b)==-a+a=0.

2. Если a+b=0, то b=0+b=(-a+a)+b=-a+(a+b)==-a+0=-a.

3. В группе кольца К по сложению (-а)+(-(-а))= -а+а. Отсюда следует равенство -(-а)=а.

4. В силу дистрибутивности умножения относительно сложения 0×а+0×а=(0+0)×а=0×а, то есть 0×а+0×а=0×а. В силу аксиомы А2 из последнего равенства следует 0×а=0.

5. В силу свойства 4 и дистрибутивности умножения относительно сложения а×b+(-а)× b=(а+(-а))× b =0× b=0, то есть а× b+(-а)× b=0. Отсюда в силу аксиомы М2 следует (-а)× b =-(а b ).

Аналогично доказывается, что a×(- b)= -(a b).

6. Из свойств 5 и 3 следует (-a)(-b)=-((-a)b)=-(-ab)=ab.

7. В силу свойства 5 и дистрибутивности умножения относительно сложения (а- b)×с=(а+(- b))×с=а×с+(- b)×с=а×с- b×с. Аналогично доказывается, что с(а- b)=с×а-с× b.

Свойства 8 и 9 доказать самостоятельно.

Определение. Пусть К=(К,+,×,1) и К'=(К',Å,Ä,1') - кольца. Говорят, что отображение j множества К в К' сохраняет операции кольца К, если выполнены условия:

1) "а,bÎK (j(a+b)=j(a)Åj(b));

2) "a,bÎK (j(a×b)=j(a)Äj(b));

Определение. Гомоморфизмом кольца К в (на) кольцо К' называется отображение множества К в (на) К', сохраняющее все операции кольца.

Гомоморфизм кольца к на кольцо к' называется эпиморфизмом.

Гомоморфизм j кольца к на кольцо к' называется изoморфизмом, если j является инъективным отображением множества К на К', то есть если отображение - биекция.

Кольца K и K' называются изоморфными (К@К'), если существует изоморфизм кольца к на кольцо к'.

Гомоморфизм j кольца к в кольцо к' называется мономорфизмом или вложением, если j является инъективным отображением множества к в к'. Гомоморфизм кольца К в себя называется эндоморфизмом кольца К. Изоморфизм кольца К на себя называется автоморфизмом кольца К. Так, например, автоморфизмом кольца является тождественное отображение кольца на себя.

Гомоморфизм колец обладает следующими свойствами:

1) если j гомоморфизм кольца к в кольцо к' , тогда образом нуля кольца к будет нуль кольца к';

2) если j гомоморфизм кольца к в кольцо к' , тогда образом элемента -аÎ к будет элемент -j(а)Î к';

3) если j гомоморфизм кольца с единицей к в кольцо к' , тогда образом единицы кольца к будет единица кольца к'.

Доказательство

1. Пусть j(0)Î к' – образ нулевого элемента кольца К. Возьмем произвольный элемент кольца aÎК и найдем его образ j(а)Î к'. Из определения кольца следует, что a+0=0+a=a, тогда так как j - отображение, j(a+0)=j(0+a)=j(a)Ûj(a)+j(0)=j(0)+j(a)=j(a). Последнее равенство означает, что элемент j(0) является нулевым для элемента j(а), а следовательно, и нулем кольца к'.

2,3. Доказать самостоятельно.

Определение. Множество L=(L,Å,Ä,1_L) называется подкольцом кольца K=(К,+,*,1_К), если LÌK и тождественное отображение множества L в К является мономорфизмом кольца L в К.

Легко показать, что любое подкольцо кольца само является кольцом. При этом нуль и единица кольца являются нулем и единицей любого его подкольца. Действительно, пусть L=(L,Å,Ä,1_L) – подкольцо кольца K=(К,+,*,1_К) и 0 – нуль кольца К. В силу условия 1 определения и свойств 1,2, L=(L,Å) – коммутативная группа и 0 – ее нулевой элемент. Умножение в L ассоциативно. Действительно, в силу условия 2 имеем aÄ(bÄc)=a*(b*c)=(a*b)*c=(aÄb) Äc для любых элементов a,b,c из L. Умножение в L дистрибутивно относительно сложения. В самом деле, по определению гомоморфизма получаем

"a,b,cÎL((aÅb)Äc=(a+b)*c=a*c+b*c=aÄcÅbÄc

Ù cÄ(aÅb)=c*(a+b)=c*a+c*b=cÄaÅcÄb.

Следовательно, L – кольцо.

Теорема. Для того, чтобы подмножество L кольца К было подкольцом кольца К, необходимо и достаточно, чтобы выполнялись следующие условия:

1) "a,bÎL (аÅbÎL);

2) "a,bÎL (а-bÎL);

3) "a,bÎL (аÄbÎL);

Доказать самостоятельно.

ИДЕАЛЫ КОЛЕЦ

Пусть к=(к,+,×) - кольцо и J - подмножество множества К. Множество J называется замкнутым в К относительно вычитания, если a-bÎJ для любых элементов а и b из J.

Множество J называется устойчивым относительно умножения справа на элементы кольца К, если akÎJ для любого aÎJ и любого kÎК, то есть если множество J вместе с каждым своим элементом а содержит все его правые кратные ak, где kÎК.

Аналогично определяется множество, устойчивое относительно умножения слева на элементы кольца к.

Множество J называется устойчивым относительно умножения на элементы кольца К, если оно устойчиво относительно умножения справа и слева на элементы кольца К.

Определение. Правым (левым) идеалом кольца К называется любое непустое подмножество множества К, замкнутое в К относительно вычитания и устойчивое относительно умножения справа (слева) на элементы кольца К.

Определение. Двусторонним идеалом кольца К, или просто идеалом кольца К, называется любое непустое подмножество множества К, если оно является одновременно правым и левым идеалом кольца к.

Из определения следует, что любой идеал J кольца К содержит нуль кольца и замкнут относительно главных операций кольца.

Множество {О_К} есть идеал кольца к, называемый нулевым идеалом.

Множество К также есть идеал кольца к. Он состоит из кратных единицы кольца, и поэтому называется единичным идеалом кольца к. Нулевой и единичный идеалы называются тривиальными идеалами кольца.

Идеалы кольца, отличные от тривиальных, называются собственными идеалами кольца к.

Примеры: Пусть z - кольцо целых чисел, K - произвольное кольцо, n фиксированное целое число. Тогда множество nZ={nx½xÎZ} является идеалом кольца Z, множество nK={nx½xÎK} является идеалом кольца к.