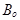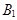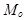Общее уравнение плоскости
1.Напомним, что вектор 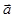 называется параллельным плоскости
называется параллельным плоскости 
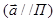 , если
, если 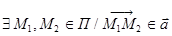 .
.
Лемма. Пусть в аффинной системе координат 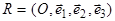 задана плоскость
задана плоскость  уравнением
уравнением
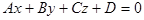 ,
, 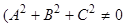 )
)
и вектор 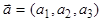 . Для того чтобы вектор
. Для того чтобы вектор 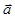 был параллелен плоскости
был параллелен плоскости  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
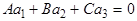 (1)
(1)
От некоторой точки 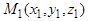 плоскости
плоскости  отложим вектор
отложим вектор 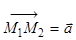 и обозначим через
и обозначим через 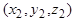 координаты точки
координаты точки 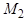 . Тогда
. Тогда
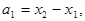
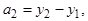
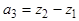 (2)
(2)
Так как 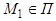 , то
, то 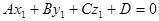 (3).
(3).
Пусть вектор 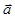 параллелен плоскости
параллелен плоскости  . Тогда точка
. Тогда точка 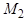 лежит в этой плоскости, поэтому
лежит в этой плоскости, поэтому
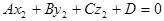 (4).
(4).
Из равенств (3) и (4) следует, что
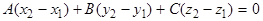 (5)
(5)
или учитывая равенства (2), получим равенство (1).
Обратно, пусть выполняется равенство (1). Подставив сюда значения 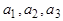 из равенства (2), получим равенство (5). Сложив равенства (3) и (5) , приходим к равенству (4). Таким образом,
из равенства (2), получим равенство (5). Сложив равенства (3) и (5) , приходим к равенству (4). Таким образом,  , то есть вектор
, то есть вектор 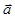 параллелен плоскости
параллелен плоскости  .‚
.‚
2.Выясним какие имеются особенности в расположении плоскости  относительно системы координат
относительно системы координат 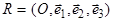 , если равны нулю некоторые из чисел
, если равны нулю некоторые из чисел 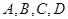 в общем уравнении плоскости
в общем уравнении плоскости
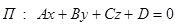 (6).
(6).
Возможны следующие случаи:
1) . 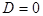 . В этом случае плоскость
. В этом случае плоскость  проходит через начало координат, так как координаты точки
проходит через начало координат, так как координаты точки 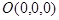 удовлетворяют уравнению (6). Обратно, если начало координат принадлежит плоскости
удовлетворяют уравнению (6). Обратно, если начало координат принадлежит плоскости  , то
, то 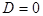
2) 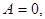
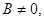
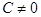 . По лемме о параллельности вектора и плоскости вектор
. По лемме о параллельности вектора и плоскости вектор 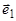 параллелен плоскости
параллелен плоскости  , поэтому плоскость
, поэтому плоскость  параллельна оси
параллельна оси 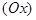 , если
, если 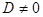 , и проходит через эту ось, если
, и проходит через эту ось, если 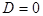
3) 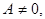
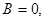
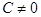 . В этом случае вектор
. В этом случае вектор 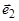 параллелен плоскости
параллелен плоскости  , поэтому плоскость
, поэтому плоскость  параллельна оси
параллельна оси 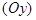 , если
, если 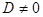 , и проходит через эту ось, если
, и проходит через эту ось, если 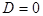
4) 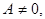
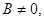
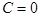 . В этом случае вектор
. В этом случае вектор 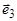 параллелен плоскости
параллелен плоскости  , поэтому плоскость
, поэтому плоскость  параллельна оси
параллельна оси 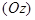 , если
, если 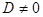 , и проходит через эту ось, если
, и проходит через эту ось, если 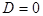
5) 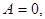
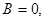
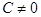 . По лемме о параллельности вектора и плоскости векторы
. По лемме о параллельности вектора и плоскости векторы 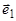 и
и 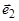 параллельны плоскости
параллельны плоскости  , поэтому плоскость
, поэтому плоскость  параллельна координатной плоскости
параллельна координатной плоскости 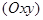 , если
, если 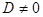 , и совпадает с этой плоскостью, если
, и совпадает с этой плоскостью, если 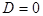 . Если
. Если 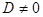 , то уравнение плоскости
, то уравнение плоскости  имеет вид:
имеет вид: 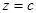 , где
, где 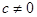 . Уравнение плоскости
. Уравнение плоскости 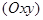 :
: 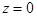 .
.
6) 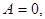
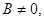
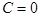 . Аналогично предыдущему плоскость
. Аналогично предыдущему плоскость  параллельна координатной плоскости
параллельна координатной плоскости 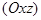 , если
, если 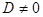 , и совпадает с этой плоскостью, если
, и совпадает с этой плоскостью, если 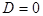 . Если
. Если 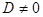 , то уравнение плоскости
, то уравнение плоскости  имеет вид:
имеет вид: 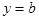 , где
, где 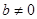 . Уравнение плоскости
. Уравнение плоскости 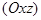 :
: 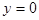 .
.
7) 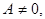
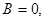
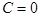 . Аналогично предыдущим двум случаям плоскость
. Аналогично предыдущим двум случаям плоскость  параллельна координатной плоскости
параллельна координатной плоскости 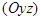 , если
, если 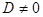 , и совпадает с этой плоскостью, если
, и совпадает с этой плоскостью, если 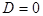 . Если
. Если 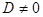 , то уравнение плоскости
, то уравнение плоскости 
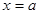 , где
, где 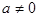 . Уравнение плоскости
. Уравнение плоскости 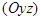 :
: 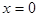 .
.
§ 10. Геометрический смысл знака трехчлена 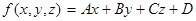
Пусть в пространстве задана аффинная система координат 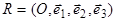 . Рассмотрим многочлен первой степени
. Рассмотрим многочлен первой степени
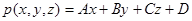 .
.
Тогда фигура 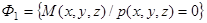 есть плоскость
есть плоскость  .
.

 Плоскость
Плоскость  разделяет множество не принадлежащих ей точек пространства на две части, каждая из которых вместе с плоскостью
разделяет множество не принадлежащих ей точек пространства на две части, каждая из которых вместе с плоскостью 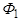 образует полупространство, ограниченное этой плоскостью.
образует полупространство, ограниченное этой плоскостью.
| Пусть 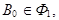
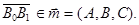 Так как Так как 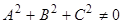 , то вектор , то вектор 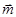 не параллелен плоскости не параллелен плоскости 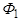 и и 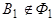 и , следовательно, точка и , следовательно, точка 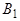 принадлежит только одному из указанных полупространств. принадлежит только одному из указанных полупространств.
|
Через точку 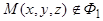 проведем прямую параллельно
проведем прямую параллельно 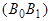 и обозначим через
и обозначим через 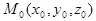 точку пересечения этой прямой с плоскостью
точку пересечения этой прямой с плоскостью 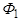 . Так как векторы
. Так как векторы 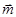 и
и 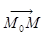 коллинеарны , то по теореме о коллинеарных векторах существует такое число
коллинеарны , то по теореме о коллинеарных векторах существует такое число 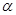 , что
, что 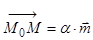 , или в координатах:
, или в координатах:
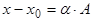 ,
, 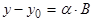 ,
, 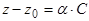 (1)
(1)
Направленные отрезки 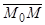 и
и 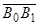 одинаково направлены (точки
одинаково направлены (точки 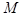 и
и 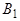 - в одном полупространстве, ограниченном плоскостью
- в одном полупространстве, ограниченном плоскостью 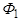 ) тогда и только тогда, когда
) тогда и только тогда, когда 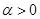 . Эти отрезки противоположно направленны (точки
. Эти отрезки противоположно направленны (точки 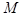 и
и 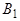 - в разных полупространствах, ограниченном плоскостью
- в разных полупространствах, ограниченном плоскостью 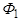 ) тогда и только тогда, когда
) тогда и только тогда, когда 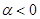 .
.
Рассмотрим многочлен 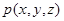 и подставим вместо
и подставим вместо 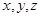 их значения из равенств (1):
их значения из равенств (1):
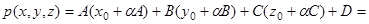
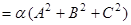 так как
так как 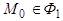 .
.
Так как 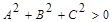 , то знак
, то знак 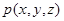 совпадает со знаком
совпадает со знаком 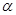 . Следовательно,
. Следовательно, 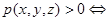
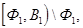 где
где 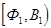 - полупространство, ограниченное плоскостью
- полупространство, ограниченное плоскостью 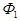 и содержащее точку
и содержащее точку 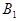 .
.
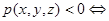
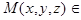
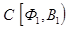 .
.
Таким образом, получаем:
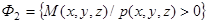 =
= 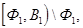
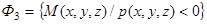 =
= 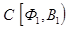 .
.
Дата добавления: 2020-10-25; просмотров: 196;