Отделение кратных множителей
Пусть многочлен f(x)=anxn+an-1xn-1+…+a1x+a0 – задан над полем Р нулевой характеристики. Многочлен f’(x)= nanxn-1+ (n-1)an-1xn-2+…+2a2x+a1 будем называть первой производной многочлена f(x). Производная многочлена f’(x) называется второй производной многочлена f(x). Легко показать, что данное определение приводит к тому же результату, что и нахождение производной функции f(x) по правилам дифференцирования.
Теорема 14. k-кратный неприводимый множитель многочлена f(x) является неприводимым множителем его производной кратности k-1.
Доказательство. Пусть р(х) - k-кратный неприводимый множитель многочлена f(x), то есть рk(х)çf(x), а рk+1(х) не делит f(x). По определению делимости многочленов можем записать f(x)= рk(х) g(x) и (р(х), g(x))=1. Найдем производную по правилам дифференцирования:
f’(x)= (рk(х) g(x))’=(рk(х)))’g(x)+ рk(х)(g(x))’=kрk-1(х)р’(х)g(x)+ рk(х)g’(x)=
=рk-1(х)(kр’(х)g(x)+ р(х)g’(x)). Так как deg p(x)>deg p’(x), то p(x) не делит p’(x), следовательно, по теореме 10 (p(x), p’(x))=1 и по условию (р(х), g(x))=1, тогда по теореме 8 имеем (p(x),g(x)p’(x))=1. Таким образом, p(x) делит второе слагаемое и не делит первое, следовательно, не делит сумму, но тогда, по определению делимости многочленов, рk-1(х) çf’(x), а рk(х) не делит f’(x), что и требовалось доказать.
Замечание. Если р(х) неприводимый множитель многочлена f(x) кратности 1, то р(х) не является делителем его производной. Из теорем 12, 13, 14 получаем, что если f(x)= p1k1(x)p2k2(x)… psks(x), то f’(x)=p1k1-1(x)p2k2-1(x)… psks-1(x)g(x), причем ни одно pi(x) не делит многочлен g(x), тогда
(f(x),f’(x))=p1k1-1(x)p2k2-1(x)… psks-1(x).
Отсюда получаем алгоритм отделения k-кратных неприводимых множителей многочлена f(x):
1) найти f’(x);
2) найти (f(x),f’(x))=d(x);
3) построить вспомогательный многочлен v(x)= 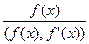 ;
;
4) многочлен v(x), если возможно, разложить на произведение неприводимых множителей;
5) определить кратность каждого из полученных множителей в разложении f(x).
Пример. Разложить многочлен f(x)=x6-6x4-4x3+9x2+12x+4 на неприводимые множители над полем рациональных чисел.
Решаем по предложенному алгоритму:
f’(x)=6x5-24x3-12x2+18x+12.
 НОД найдем по алгоритму Евклида.
НОД найдем по алгоритму Евклида.
6x5-24x3-12x2+18x+12
x6-6x4-4x3+9x2+12x+4 x5-4x3-2x2+3x+2
x6-4x4-2x3+3x2+2x x
-2x4-2x3+6x2+10x+4
x5-4x3-2x2+3x+2 x4+x3-3x2-5x-2
x5+x4-3x3-5x2-2x x-1
-x4-x3+3x2+5x+2
-x4-x3+3x2+5x+2
d(x) = (f(x),f’(x))= x4+x3-3x2-5x-2. Строим вспомогательный многочлен v(x)
 x6-6x4-4x3+9x2+12x+4 x4+x3-3x2-5x-2
x6-6x4-4x3+9x2+12x+4 x4+x3-3x2-5x-2
x6+x5-3x4-5x3-2x2 x2-x-2
-x5-3x4+x3+11x2+12x+4
-x5-x4+3x3+5x2+2x
-2x4-2x3+6x2+10x+4
-2x4-2x3+6x2+10x+4
v(x)= x2-x-2=(x-2)(x+1)
Чтобы определить кратность каждого множителя, разделим f(x) на двучлены (x-2) и (x+1) по схеме Горнера.
| -6 | -4 | ||||||
| х=-1 | -1 | -5 | |||||
| х=-1 | -2 | -3 | |||||
| х=-1 | -3 | ||||||
| х=-1 | -4 | ||||||
| | | | | ||||
| х=2 | -2 | ||||||
| х=2 |
Получили следующий результат f(x)= (x+1)4(x-2)2 .
Замечание. При решении данной задачи мы не только разложили многочлен на неприводимые множители. Из полученного разложения легко находим корни многочлена х=-1 и х=2. Следует обратить внимание, что f(x) делится на (х+1) четыре раза, говорят, что х=-1 – корень кратности четыре, аналогично, х=2 - корень кратности два. И в общем случае:
aÎР называется k-кратным корнем многочлена f(x)ÎР[x], если (х-a)kçf(x), а (х-a)k-1 не делит f(x).
Очевидно, для нахождения кратных корней можно использовать тот же алгоритм.
Дата добавления: 2020-10-25; просмотров: 1815;











