Метод простой итерации для решения систем линейных уравнений

Приведем систему (1) к равносильной ей системе вида:

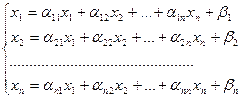(7)

или в сокращенной записи , 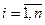(8)

О системе (7) говорят, что она «приведена к нормальному виду».

Правая часть системы (7) определяет отображение

F: , , 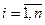(9)

преобразующее точку 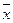(x₁, x₂, … , x_n) п-мерного векторного пространства в точку (у₁, у₂, … ,у_n) того же пространства. Используя отображение (9) и выбрав начальную точку , можно построить итерационную последовательность точек п-мерного пространства (аналогично методу простой итерации для уравнения x = f(x)):

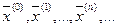(10)

Если отображение F является сжимающим, то эта последовательность сходится и ее предел является решением системы (7), и тем самым исходной системы.

Рассмотрим условия, при которых отображение (9) является сжимающим. Решение этого вопроса зависит от способа метризации пространства.

Пусть 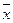(x₁, x₂, … , x_n) и (у₁, у₂, … ,у_n) – две точки п-мерного пространства. Для применения метода итераций систему линейных уравнений удобно «погрузить» в пространство с одной из следующих метрик:

1) ρ₁( , ) =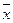

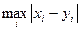
2) ρ₂( , ) =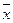

3) ρ₃( , ) =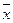

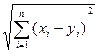
Отображение (9) будет сжимающим, если выполняется хотя бы одно из условий:

а) в пространстве с метрикой ρ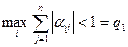₁: (11)

б)в пространстве с метрикой ρ₂: (12)

в) в пространстве с метрикой ρ₃: (13)