Кинематическая и расчетная схема механической части электропривода

Непосредственное представление о движущихся массах электромеханической системы и механических связях между ними дает кинематическая схема, примеры которой для различных механизмов приведены на рис. 5.1.

Каждый i-ый вращательно движущийся элемент характеризуется моментом инерции J_i и связан с (i+1)-м элементом механической связью, обладающей в общем случае жесткостью с_i. Соответственно каждый j-ый поступательно движущийся элемент имеет массу m_j и связан со следующим механической связью с жесткостью c_j. Из рис. 5.1 видно, что наряду с механической жесткостью каждого из элементов кинематическая схема не отражает того, что: в общем случае инерционные массы системы движутся с различными скоростями, а также в элементах механической части могут иметься зазоры.

Поэтому для анализа условий движения механической части электромеханических систем пользуются расчетными механическими схемами, составленными на основе кинематических схем. На рис. 5.2 приведена расчетная схема механической части электропривода подъема, соответствующая кинематической схеме, изображенной на рис. 5.1, г.

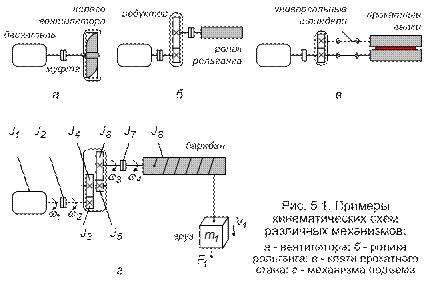
Рис. 5.2. Расчетная схема механической части механизма подъема

При составлении расчетных механических схем учитывается, что различные элементы системы могут двигаться с различными скоростями, поэтому непосредственно сопоставлять их моменты инерции J_i и массы m_j, жесткости связей

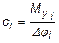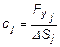и (5.1)

невозможно. В выражениях (5.1) 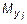, 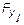– нагрузка (момент и сила) упругой механической связи; 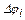, – деформация упругого элемента при вращательном и поступательном движениях. В связи с этим выполняют приведение всех параметров элементов кинематической цепи к одной расчетной скорости (обычно к скорости вращения электродвигателя):

- для момента инерции (вращающейся массы)

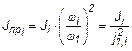; (5.2)

- для поступательно движущейся массы

; (5.3)

- для жесткостей упругих механических связей

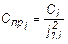и ; (5.4)

- для моментов и сил нагрузк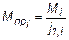и

и 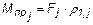; (5.5)

- для вращательных и поступательных перемещени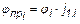й

и 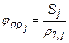. (5.6)

В выражениях (5.2)-(5.6) – угловая скорость вала элемента кинематической цепи, к которой осуществляется приведение параметров (например, вала двигателя); – передаточное число от вала приведения к i-му валу кинематической схемы; 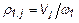– радиус приведения j-го поступательно движущегося элемента к скорости звена приведения ; 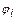, 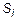– вращательное (угол поворота вала) и поступательное перемещения. Причем условием соответствия приведенной расчетной схемы к реальной электромеханической системе является выполнение закона сохранения энергии.

Суммарные, приведенные к валу двигателя момент инерции и момент сопротивлений можно подсчитать по зависимостям

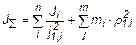, (5.7)

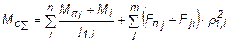, (5.8)

где n, m – число элементов соответственно вращающихся и движущихся поступательно; , – моменты и силы потерь в i-ом вращающемся или j-ом поступательно движущемся элементе.

Следует отметить, что все многообразие совершенно разнотипных механизмов могут быть приведены к 3-м типичным расчетным схемам (см. рис. 5.3): трех- и двухмассовой упругим системам или одномассовой абсолютно жесткой системе.

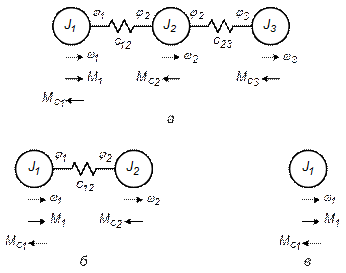
Рис. 5.3. Типовые расчетные механические схемы:

а – трехмассовая упругая; б – двухмассовая упругая;

в - одномассовая абсолютно жесткая

При рассмотрении электромеханических систем трехмассовая упругая система используется в редких случаях, когда возникает необходимость детального анализа условий движения. Двухмассовая упругая система – наиболее часто встречающееся представление промышленных электромеханических систем. Для простых механизмов, не имеющих в своей кинематике длинных валов при расчетах можно пользоваться одномассовым представлением механической части.