Пассивные эксперименты

Особенностью пассивного эксперимента являться то, что экспериментатор не может активно воздействовать на исследуемый объект, а сам эксперимент сводится к сбору измерительной информации и ее оптимальной обработке.

Задачей пассивного эксперимента чаще всего является построение математической модели объекта. В зависимости от того, как зависят друг от друга факторы и отклики, модель может быть представлена в виде функциональной зависимости (детерминированная модель) или в виде некоторой диффузной модели, параметры которой могут быть только оценены, т.к. вычисляются на основе статистического материала.

В результате пассивного эксперимента экспериментатор получает пары чисел x_i® y_i ( 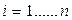), которым на плоскости 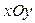соответствуют точки (рис.2.10). Совокупность всех экспериментальных точек образует поле корреляции.

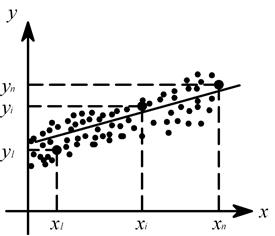
Рис. 2.10. Графическое изображение уравнения регрессии y=f(x)

Учитывая вероятностный характер полученных данных, предполагаемую зависимость 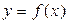можно рассматривать только как зависимость математического ожидания 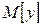от .

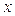При исследовании статистически связанных зависимостей сталкиваются с двумя случаями.

В первом случае экспериментатор задает (или просто фиксирует) вполне определенным, детерминированные значения независимой переменной 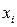, для которых наблюдается соответствующие случайные значения 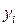, определяемые своими статистическими характеристиками: оценкой математического ожидание и СКО. В этом случае модель называется регрессионной.

Во втором случае наблюдаемые значения 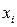и 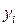представляют собой элементы выборки, т. е. независимая переменная х сама является случайной величиной и может быть охарактеризована соответствующими оценками. Модель такого вида связи называется корреляционной.

Пусть случайная величина y зависит от одной или нескольких неслучайных величин .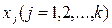

Уравнением регрессии называют функциональную зависимость математического ожидания М[y] от 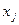, т. е.

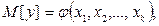
а регрессивным анализом - процедуру построения уравнения регрессии и анализ его с помощью аппарата математической статистики. Он включает операции оценивания независимых параметров модели, проверки их статистической значимости, проверки адекватности полученной модели исходному статистическому материалу и т. п.

Видом (структурой) уравнения задаются заранее, исходя из физической сущности изучаемого явления, анализа накопленного статистического материала, на основании априорной информации. Поэтому непосредственной задачей регрессионного анализа является статистическое оценивание неизвестных параметров постулированной модели.

Структура модели определяется видом функции 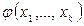. Если эта функция линейна относительно параметров, то говорят о линейной модели регрессии, если - нет, то модель называется нелинейной.

Простая регрессия предполагает наличие одной независимой и одной зависимой переменной т. е.

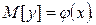
Если число независимых переменных несколько, то регрессия называется множественной.

Методами регрессионного анализа можно решать следующие задачи:

· описание и установление возможной причинной связи между переменными;

· предсказание (экстраполяцию) зависимой переменной по значениям независимой переменной;

Рассмотрим простую регрессионную связь.

Пусть в результате однофакторного эксперимента получен статистический материал, т. е. выполнено n пар измерений единственного входного сигнала 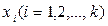и соответствующих значений .

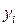Будем искать математическую модель регрессионной связи в виде степенного полинома

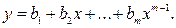(2.43)

где 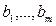–искомые параметры модели.

Известно [2.8], что при правильном выборе степени полинома m такая модель позволяет достаточно точно аппроксимировать истинную зависимость.

В соответствии с (2.43) для i-го результата (точки) можно записать

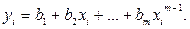(2.44)

Поскольку измерение 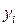выполнены с погрешностями, то результат i-го измерения можно записать в виде

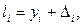
или

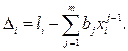
Используя МНК, т. е. выполняя условие

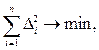
получим систему уравнений, линейную относительно искомых параметров j

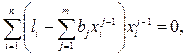(2.45)

решая которую, получим оценки параметров 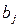постулированной регрессионной модели.

Очевидно, что полученная модель

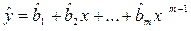(2.46)

может лишь с той или иной точностью соответствовать экспериментальной совокупности 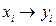, т. к. МНК не гарантирует точного совпадения отклика, вычисленного по (2.46) и полученного экспериментально, а только утверждает, что 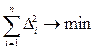. Поэтому заключительным этапом анализа является установление адекватности полученной регрессионной модели экспериментальным данным.

В качестве меры адекватности может быть использован коэффициент корреляции [2.3].

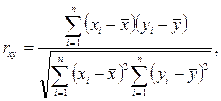(2.47)

чем ближе 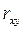к единице, тем ближе экспериментальные точки к (2.46). Другой мерой адекватности модели является оценка дисперсии ошибки, F – критерий и др. Более подробно анализ качества полученной модели будет рассмотрен в теме «Активные эксперименты».