Совместные и совокупные измерения

Эти измерения характеризуются тем, что значения искомых величин находят из решения системы уравнений, которые связывают искомые величины с некоторыми другими, получаемыми в результате эксперимента посредством прямых или косвенных измерений.

Если измеряемые величины - одноименные, измерения называются совокупными, если неодноименные – совместными.

Целью таких измерений обычно является установление функциональной зависимости между измеряемыми величинами. Это возможно путем замены экспериментальных данных значениями некоторой теоретической функции. Если замена справедлива для всех значений аргумента в заданном интервале, то заменяющую функцию называют аппроксимирующей. Если замена справедлива только для некоторых, дискретных значений аргумента –функцию называют интерполирующей.

Очевидно, что подобные задачи должны решаться в два этапа:

· выбор структуры предполагаемой зависимости, т. е. выбор вида математической модели (линейная, полиномиальная, экспоненциальная и т. п.);

· вычисление параметров (коэффициентов) этой модели.

В связи с этим, при выполнении совместных измерений, во-первых, возникает задача выбора аппроксимирующее зависимости 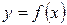так, чтобы она наилучшим образом описывала истинную зависимость, во-вторых, необходимо ответить на вопрос – действительно ли выбранная функция наилучшим образом приближается к искомой зависимости и какой мерой можно оценить близость экспериментальной зависимости к истинной.

Одним из возможных вариантов решения подобных задач это применение метода наименьших квадратов (МНК).

В этом методе оценки параметров выбранной модели определяют из условия, что сумма квадратов отклонений расчетных значений аппроксимирующей функции от экспериментальных значений должна быть минимальна. При этом полагают, что результаты измерений удовлетворяет условиям:

· значения аргументов известны точно;

· систематические погрешности из 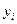исключены, а результаты измерений 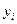содержат только случайные составляющие погрешности, которые независимы, имеют одинаковые дисперсии и распределены по нормальному закону.

При выполнении этих условий МНК дает несмещенные оценки параметров модели, имеющие минимальные дисперсии.

Пусть искомые значения величин 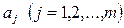находятся из решения системы линейных уравнений:

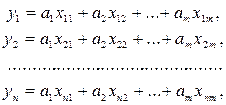(2.35)

здесь 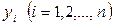–измеряемые значения величины 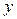, 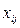–известные значения аргумента.

Систему уравнений (2.35) перепишем в виде

(2.36)

Так как измерены с некоторой погрешностью 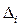то действительный результат измерения 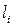будет иметь вид

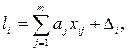(2.37)

или

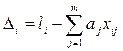
В соответствии с МНК наилучшие оценки для 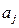должны соответствовать условию

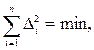
или

. (2.38)

Это условие выполняется, если все частные производные от (2.38) по искомым параметрам 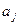будут равны нулю, т. е.

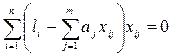. (2.39)

Система уравнений (2.39) линейна относительно 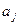, решая ее известными методами определяем искомые параметры постулируемой модели (2.35). Оценки параметров 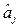является состоятельными, несмещенными и эффективными.

Оценка дисперсии случайной погрешности согласно [2.8] будет равна

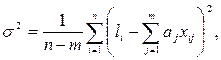(2.40)

здесь 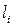– измеренные величины, соответствующие ; 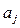–коэффициенты, найденные по (2.39).

При обработке экспериментального материала с целью определения функции преобразования в качестве математической модели часто выбирают полином вида:

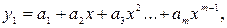
а задачей самого измерения является определение коэффициентов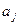

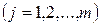
Пусть в результате эксперимента получено n пар чисел 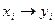, тогда результат измерений можно представить в виде

(2.41)

Тогда в соответствии с МНК и учетом (2.39) получим:

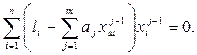(2.42)

Решение этой системы, линейной относительно 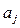, дает значение оценок этих коэффициентов.

Пример. В процессе измерения получены данные 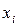и .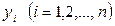

В качестве модели, описывающей взаимосвязь 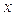и 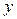, выберем зависимость

.

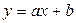Необходимо найти оценки коэффициентов а и b, наилучшим образом соответствующие экспериментальные данным.

Погрешность интерполяции для i–ой точки

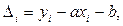
а условие выполнения МНК

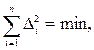
т.е.

.

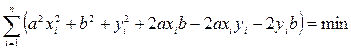Условие минимума выполняется, если

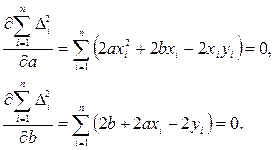
или

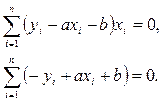
Решая эту систему можно определить оценки искомых коэффициентов а и b. Эти оценки будут наилучшими в смысле минимума отклонений предполагаемой функциональной зависимости от экспериментальных данных.