Релейные схемы. Связь их физической структуры и функций проводимости с алгеброй логики
Анализ и синтез релейных управляющих схем
Релейные схемы (РС) являются одними из наиболее простых и распространенных в технике устройств управления. Отличительно особенностью РС является дискретный логический принцип срабатывания их элементов, реагирующих на внешние воздействия по принципу ”включен - выключен”. Это позволяет при анализе существующих схем и проектировании новых использовать методы алгебры логики.
Релейные схемы. Связь их физической структуры и функций проводимости с алгеброй логики
Со структурной точки зрения в РС можно выделить входы` а =(а1, ... аn ), задающие внешние воздействия на схему, выходы`f = (f1, ..., fm ), а также само релейное устройство (РУ):
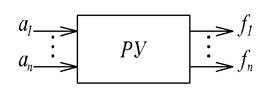
Рис.1.7
Значения компонент аi,¦j векторов`а и`¦ изменяются скачкообразно, принимая два состояния, которые можно без ограничения общности закодировать с помощью 0 и 1. Обычно при отсутствии тока состояние кодируют нулем, а после достижения порогового значения - единицей.
РУ состоят из дискретно срабатывающих релейных элементов (РЭ), реагирующих на внешние воздействия, и соединений между ними, а также с входами и выходами РС. Будем рассматривать РС наиболее простого типа с одним входом и одним выходом. Обычно их назначение заключается в подаче питания на исполнительный электродвигатель.
Релейные элементы по принципу действия делят на контактные и бесконтактные. В первых набор контактов замыкается либо размыкается при механическом нажатии на некоторый переключатель. В бесконтактных РЭ положение контактов изменяется при наличии электрических, магнитных, тепловых и других воздействий заданного уровня.
Поскольку с точки зрения анализа и синтеза РС конструктивное исполнение РЭ несущественно, будем обозначать последние в виде механических реле, содержащих две группы контактов – нормально замкнутых и нормально разомкнутых.
На рис.1.8 схематически показан РЭ, обозначенный Х и имеющий оба вида контактов: х1 – нормально разомкнутый (в свободном состоянии проводимость отсутствует, при нажатии на кнопку - появляется) и х2 – нормально замкнутый (в свободном состоянии проводимость есть, в нажатом - отсутствует). С точки зрения булевой алгебры контакту х1 соответствует тождественная функция х, поскольку в нем проводимость совпадает с наличием внешнего воздействия. Контакт х2 реализует функцию отрицания`x, так как при отсутствии воздействия проводимость у него есть, а при нажатии на переключатель цепь разрывается.
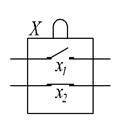
Рис.1.8
Функционирование РУ полностью определяется состоянием РЭ, входящих в них, и способом их соединения между собой. Пусть РС содержит n РЭ. Обозначим их Х1, … , Хn. Нормально разомкнутым контактам каждого реле Хi (1£ i £ n) ставим в соответствие переменную хi, нормально замкнутым контактам Хi - отрицание`хi. Различные контакты одного реле, принадлежащие к одной группе (замкнутые или разомкнутые), входят в разные цепи и если по одним проводимость есть, то по другим ее может не быть. Обозначим проводимость в общей цепи от входа к выходу РС через ¦. Если общая цепь замкнута, то ¦ = 1, иначе ¦ = 0.
При таком способе кодирования текущего состояния контактов РЭ и общей проводимости в РС ¦ последняя является булевой функцией переменных х1, ... , хn и их отрицаний. Поскольку РС в большинстве своем представляют электрические схемы, то данное отображение ¦(х1, ... , хn) обычно называют функцией проводимости.
Таким образом, функциональные свойства РС с одним входом и одним выходом однозначно описываются её булевой функцией проводимости ¦(х1, ... , хn).
Рассмотрим, каким образом характер соединений между контактами РЭ определяет функцию проводимости. На рис.1.9 показано последовательное соединение двух контактов Х и Y. Каждый из них может быть как замкнутым, так и разомкнутым. Схема реализует логическую операцию умножения &, так как функция проводимости равна единице тогда и только тогда, когда одновременно есть проводимость в обоих контактах Х и Y.
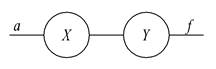
Рис.1.9
В случае параллельного соединения (рис.1.10) контактов схема реализует логическое сложение «ИЛИ», поскольку для выполнения условия ¦ = 1 достаточно выполнения хотя бы одного из условий Х =1 либо Y =1.
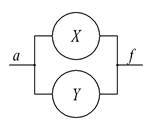
Рис.1.10
Физическая структура РС, в которой используются только параллельные и последовательные соединения, изоморфна некоторой формуле алгебры логики, отражающей наличие контактов РЭ в схеме, вид и порядок их соединения. Изоморфный характер отображения означает, что каждому нормально разомкнутому или замкнутому контакту РС взаимно однозначно соответствует своя переменная формулы либо ее отрицание, а для каждого соединения между контактами РС в формуле есть своя элементарная функция, стоящая между соответствующими выражениями формулы. На рис.1.11 приведена принципиальная схема РС, изоморфная формуле алгебры логики F(х, у) =`х & у Ú x.
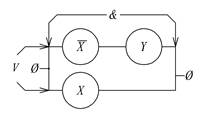
Рис.1.11
Как и в алгебре логики, где одна и та же функция может быть реализована множеством различных формул, у РС для обеспечения заданной функции проводимости могут быть использованы различные физические структуры. Поэтому все вопросы анализа, синтеза и оптимизации РС можно свести к изучению соответствующих им функций и формул в алгебре логики.
Замечание. Структура формул алгебры логики позволяет изоморфно отобразить только системы с параллельными и последовательными соединениями элементов (в данном случае – контактов РЭ). Схемы со смешанным порядком соединения элементов, которые нельзя эквивалентно преобразовать только к параллельным и последовательным соединениям, нельзя изоморфно отобразить формулами алгебры логики. Например, для схемы с 6 контактами РЭ, показанной на рис.1.12, не существует изоморфной формулы алгебры логики, содержащей 6 обозначений переменных и их отрицаний. Наиболее короткая формула для функции проводимости данной схемы, например, ¦ = x(y z Ú`y`z) Ú`x `z содержит 7 таких символов.
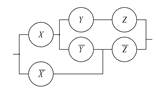
Рис.1.12
Проектирование РС
Рассмотрим проектирование физической структуры РС по заданной функции проводимости. Наиболее употребительным критерием оптимальности РС является минимальность общего числа контактов РЭ, входящих в схему, поскольку при этом повышается надежность схемы, снижается вес, габариты, себестоимость, энергопотребление.
Аналогичный критерий оптимальности был ранее рассмотрен для нормальных форм. Оптимальные по нему формы называют минимальными. Однако, если отказаться от обязательного представления формул в нормальной форме, то можно получить и более оптимальные их варианты с точки зрения уменьшения в них числа переменных. Для этого в МДНФ и МКНФ необходимо дополнительно использовать дистрибутивные законы алгебры логики, которые являются аналогами правил вынесения за скобки:
x & y Ú x & z = x &(y Ú z);
( x Ú y ) & ( x Ú z) = x Ú y & z.
Также при оптимизации схем также часто применяют правила поглощения:
x ( х Ú y ) = x ;
x Ú x y = x .
В данных законах вместо x , y , z могут быть подставлены любые формулы. При наличии нескольких вариантов использования данных законов следует выбирать те, которые обеспечивают сокращение наибольшего числа переменных в формуле.
Определение. Оптимальными в классе нормальных форм будем называть РС, соответствующие МДНФ либо МКНФ, построенным по заданной функции проводимости. Абсолютно оптимальными будем называть РС, полученные при максимальном сокращении числа переменных в соответствующих формулах.
Пример. Построить 1) оптимальную в классе нормальных форм и 2) абсолютно оптимальную РС, реализующие функцию проводимости ¦ = (01001100).
Решение.Обозначим РЭ схемы через Х, Y, Z. СДНФ функции имеет следующий вид :
¦ =`x`y z Ú x`y `z Ú x`y z .
МДНФ имеет вид: ¦ =`x`y z Ú х`y. Она содержит 5 символов переменных. Принципиальная схема РС, реализующей данную формулу будет следующей:
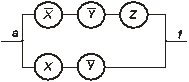
Рис.1.13
Соответствующая ей физическая схема имеет вид:
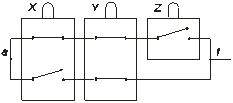
Рис.1.14
Полученная схема будет оптимальной в классе нормальных форм. Применение дистрибутивного закона к найденной выше МДНФ позволяет сократить её и даёт формулу: ¦=`y & (`x z Ú х ), которая содержит только 4 символа переменных. Следовательно, приведенная выше РС не является абсолютно оптимальной. Принципиальная и физическая схемы абсолютно оптимальной РС даны на рис.1.15 а) и б).
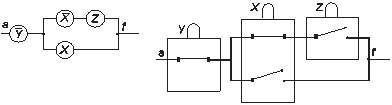
а) б)
Рис.1.15
При оптимизации физической структуры существующей РС вначале по ней строится соответствующая формула алгебры логики. Затем с использованием формульных преобразований или таблицы истинности определяется МДНФ либо МКНФ. Если необходимо, далее формула сокращается с использованием дистрибутивных и других законов алгебры логики.
Для построения оптимальных РС при частичном задании их функций проводимости вначале ЧОФ необходимо доопределить оптимальным образом.
ЗАДАЧИ
1. Построить оптимальные РС, реализующие функции:
а) х у Ú y z Ú x z ;б) х½ (у ® z) ;в) (х® у)&( y® z) ;г) х у Å xz ;д) (10011101);е) (01101110);ж) (0110100010010111) .
2. Найти функции проводимости, оптимизировать РС, схемы которых указаны на: а) рис. 1.16 ; б) рис. 1.17.
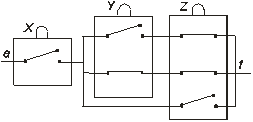
Рис.1.16
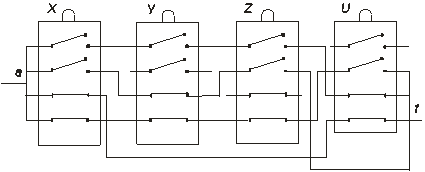
Рис.1.17
3. Построить оптимальные РС для частично определенных функций а) (0??011??) ; б) (?0?0?111) ; в) (1?0101??).
4. Обозначить РЭ, их контакты и построить РС, блокирующую главный привод аппарата в следующих случаях: а) открыт загрузочный или разгрузочный люк, б) давления в рабочей ёмкости или в рубашке отклоняются от допустимых пределов, в) рабочая ёмкость загружена менее чем на 1/4 полезного объёма.
5. Система управления приводами П1 и П2 содержит два датчика Д1 и Д2. При включенном Д1 и отключенном Д2 оба привода включаются, при включенном Д2 и отключенном Д1 включен только П1. В остальных случаях оба привода отключены. Построить управляющую РС.
6. Освещение в помещении должно включаться ровно одним из трех переключателей. Построить функцию проводимости и соответствующую РС.
Дата добавления: 2020-10-14; просмотров: 556;











