Радикальный признак Коши.
Если для ряда с положительными членами 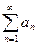
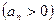 величина
величина 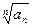 имеет конечный предел p при
имеет конечный предел p при 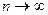 , т.е.
, т.е. 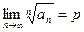 , то в случае:
, то в случае:
1) p<1, то ряд 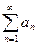 сходится;
сходится;
2) p>1, то ряд 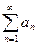 расходится;
расходится;
3) p=1 – вопрос о сходимости ряда 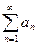 остается открытым.
остается открытым.
Доказательство:
Пусть p<1, рассмотрим число q, удовлетворяющее соотношению p<q<1.
Начиная с некоторого номера n = N ,будет иметь месть соотношение
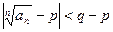
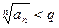 ,
, 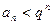
При q<1 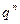 - убывающая геометрическая прогрессия. Если, начиная с номера N
- убывающая геометрическая прогрессия. Если, начиная с номера N 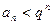 , то из условия сходимости ряда
, то из условия сходимости ряда 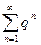 следует сходимость ряда
следует сходимость ряда 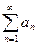 .
.
Пример. Исследовать сходимость ряда 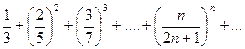 .
.
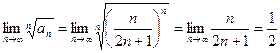 .
.
Интегральный признак Коши.
Пусть 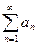 - ряд с положительными членами, для которого существует положительная, непрерывная и монотонно убывающая функция на
- ряд с положительными членами, для которого существует положительная, непрерывная и монотонно убывающая функция на 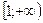 , такая, что
, такая, что 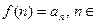 . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:
1) если несобственный интеграл 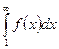 сходится, то и ряд
сходится, то и ряд 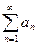 тоже сходится;
тоже сходится;
2) если несобственный интеграл 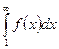 расходится, то и ряд
расходится, то и ряд 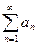 тоже расходится.
тоже расходится.
Пример. Исследовать на сходимость ряд 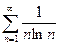
Решение.
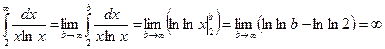 , т.к. несобственный интеграл расходится, то и расходится соответствующий ему ряд
, т.к. несобственный интеграл расходится, то и расходится соответствующий ему ряд 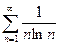 .
.
Дата добавления: 2020-10-14; просмотров: 471;











