Электрическая цепь и ее элементы

Электрической цепью называется совокупность устройств, предназначенных для передачи, распределения и взаимного преобразования электромагнитной, тепловой, световой и других видов энергии, если процессы, протекающие в устройствах, могут быть описаны при помощи таких понятий, как ЭДС, напряжение и ток.

Основными элементами электрической цепи являются источники и приемники электрической энергии, которые соединяются между собой проводниками. В источниках электрической энергии (аккумуляторы, гальванические элементы, генераторы и т.п.) химическая, механическая, тепловая и другие виды энергии преобразуются в электрическую энергию. В приемниках энергии (нагреватели, электрические машины, осветительные приборы и т.п.) электрическая энергия преобразуется в иные виды энергии.

Электрические цепи, в которых получение, передача и преобразование электрической энергии происходит при постоянных во времени токах и напряжениях, называются цепями постоянного тока, а при переменных во времени токах и напряжениях – цепями переменного тока.

Для расчета и исследования процессов, протекающих в электрической цепи, ее заменяют расчетной схемой замещения, т.е. идеализированной цепью, которая служит расчетной моделью реальной цепи. При получении такой схемы каждый реальный элемент цепи заменяется расчетной моделью – элементом схемы. Математическое описание каждого элемента должно отражать основные протекающие в нем физические процессы.

Одним из приемников электрической цепи является резистивный элемент – резистор. В резистивном элементе с сопротивлением R электрическая энергия необратимо преобразуется в другие виды (тепловую, механическую, энергию излучения и т.п.), чаще всего в тепло. Величина активного сопротивления измеряется в Омах (Ом). Мгновенная мощность, с которой происходит преобразование энергии, определяется соотношением: p = i²R. Резистивные (или активные) сопротивления вводятся в схемы замещения других элементов цепи для учета необратимого преобразования электромагнитной энергии в другие виды.

Для расчета токов и напряжений в цепи задаются положительные направления токов и напряжений. Положительным направлением тока и напряжения полагается их направление от узла с большим потенциалом к узлу с меньшим потенциалом.

На рис. 1.1 φ₁(t) ≥ φ₂(t), поэтому направление тока и напряжения (падения напряжения) задано от узла с потенциалом φ₁(t) к узлу с потенциалом φ₂(t). В резистивном элементе напряжение связано с током законом Ома:

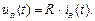(1.1)

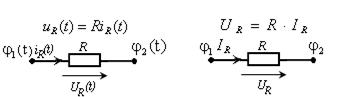
а б

Рис. 1.1. Токи и напряжения на участке цепи

Для цепи постоянного тока (рис. 1.1, б) или для действующих значений резистивной цепи с гармоническими источниками U_R = R · I_R. Если значение сопротивления резистора не зависит от тока, протекающего через него, то такой резистор называется линейным, а электрическая цепь, состоящая только из таких резисторов, – линейной резистивной.

В первой лабораторной работе рассматриваются цепи, содержащие только линейные элементы (резисторы и источники ЭДС и тока).

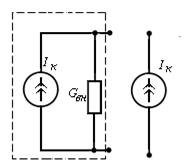
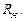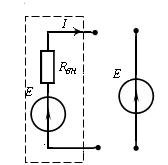
Источником напряжения (ЭДС, тока) называют источник, напряжение (ЭДС, ток) которого не зависит от сопротивления внешней цепи Схемы замещения реальных источников приведены на рис. 1.2: источник ЭДС (напряжения) – на рис. 1.2, а, источник тока – на рис. 1.2, б. Величина ЭДС источника (Е) измеряется в режиме холостого хода (т.е. при токе в источнике I_k = 0) и равна напряжению на его зажимах. В схемах замещения источников резистор R_вн = 1/G_вн учитывает тепловые потери энергии, выделяемые внутри источника. Если внутреннее сопротивление источника ЭДС (напряжения) равно нулю, а источника тока – бесконечности, то такие источники называют идеальными (рис. 1.2, б, г).

а б	в г
Рис. 1.2. Идеальные и реальные источники энергии

В реальных источниках внутреннее сопротивление R_вн имеет конечное значение, поэтому на практике за источник ЭДС (напряжения) принимают источник, для которого выполняется условие 10R_вн ≤ R_н ≤ ∞, а при условии 0 ≤ R_н ≤ 0,1R_вн – за источник тока, где R_н – сопротивление нагрузки, к которому подключен источник.

Источники напряжения, ЭДС и тока характеризуются внешними вольт-амперными характеристиками (ВАХ): для источников напряжения и ЭДС – зависимостями напряжения или ЭДС от тока, протекающего через источник, а для источника тока – зависимостями тока от напряжения на его зажимах. На рис. 1.3, а, в показаны внешние характеристики реальных источников ЭДС и тока, где имеются линейный (рабочий, с небольшим наклоном) и нелинейный (с резким изменением) участки характеристик, на которых источник может выйти из строя. На рис. 1.3, б, г изображены внешние характеристики идеальных источников ЭДС и тока. В данной работе рассматриваются источники, которые работают на линейном участке характеристики.

а б в г

Рис. 1.3. Вольт-амперные характеристики источников энергии

Законы Кирхгофа

Для любой электрической цепи справедливы законы Кирхгофа для токов и напряжений.

Узлом в электрической цепи называется место соединения трех и более ветвей. Место соединения двух ветвей называется устранимым узлом.

Первый закон Кирхгофа: алгебраическая сумма токов в проводниках, соединенных в узел, равна нулю:

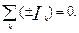(1.2)

В (1.2) ток берется со знаком плюс, если он втекает в узел, и со знаком минус, если вытекает.

Ветвью называется участок цепи между двумя узлами, состоящий только из последовательно соединенных элементов. Замкнутым контуром цепи называется путь по ветвям цепи, который начинается и заканчивается в одном и том же узле, при прохождении которого ни один из элементов не проходится дважды. Контура называются взаимно независимыми, если в каждом из них есть хотя бы одна ветвь, которой нет в других контурах.

Второй закон Кирхгофа: алгебраическая сумма ЭДС всех источников в любом замкнутом контуре цепи равна алгебраической сумме напряжений на остальных элементах того же контура:

 

(1.3)

Для составления уравнения необходимо задать направление обхода контура (по направлению часовой стрелки либо против). В (1.3) ЭДС и напряжения берутся со знаком плюс, если их направления совпадают с направлением обхода контура, если не совпадают, то со знаком минус. Падения напряжения в (1.3) могут быть по закону Ома выражены через токи и сопротивления.

Система независимых контуров выбирается так, что в контур включаются только ветви с неизвестными токами, а в каждый последующий контур должна входить хотя бы одна ветвь с неизвестным током, не вошедшая в предыдущие контуры.

 

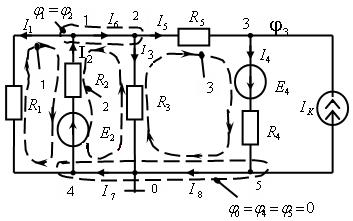
Рис. 1.4. Разветвленная электрическая цепь

 

Для нахождения токов в электрической цепи методом уравнений Кирхгофа составляется система уравнений из 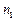уравнений по первому закону Кирхгофа и 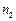уравнений по второму закону Кирхгофа.

 

 

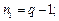
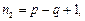
где q – число узлов в схеме;

р – число ветвей в схеме, не содержащих источники тока.

Так, для схемы рис. 1.4 точки 1 и 2 представляют собой один узел, а точки 4, 0 и 5 – другой.

q = 3; p = 5; n₁ = 2; n₂ = 3.

 

Составлены системы уравнений:

- по первому закону Кирхгофа для двух верхних узлов:

 

 

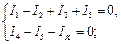
- по второму закону Кирхгофа для контуров 1–3:

 

 

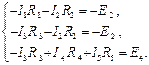
Решая систему уравнений, можно определить токи в ветвях.

 

<1234567>

---

Дата добавления: 2020-10-14; просмотров: 337;

---