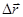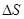Эти уравнения движения эквивалентны векторному уравнению
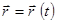 . (2)
. (2)
Модуль радиус – вектора 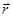 в данный момент времени определяется из выражения:
в данный момент времени определяется из выражения:
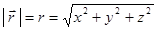 (3)
(3)
Исключая t в уравнении (1) получим уравнение траектории движения.
Пример: Пусть кинематические уравнение движения точки заданы в форме:

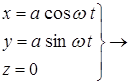
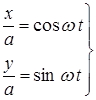 +
+ 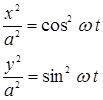
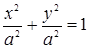
где w = const.
Т.о. уравнение траектории имеет вид:
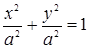 - это уравнение окружности радиусом
- это уравнение окружности радиусом 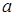 .
.
Т.е. точка движется в плоскости z = 0 по окружности.
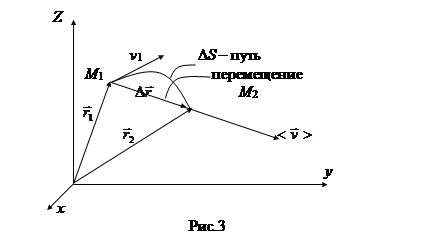
Рассмотрим движение м.т. вдоль произвольной траектории (рис.3).
 |
Пусть в момент времени 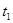 м.т. находится в положении
м.т. находится в положении 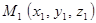 , характеризуемом радиус – вектором
, характеризуемом радиус – вектором 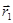 ; в момент времени
; в момент времени 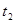 - в положении
- в положении 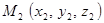 , характеризуемом радиус – вектором
, характеризуемом радиус – вектором 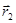 . Т.о., за промежуток времени
. Т.о., за промежуток времени 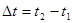 м.т. прошла криволинейный отрезок Ds.
м.т. прошла криволинейный отрезок Ds.
Расстояние между двумя геометрическими точками, отсчитанное вдоль траектории движущейся м.т. называется путём.
Путь s является скалярной функцией времени, измеряется в метрах (м).
Вектор
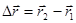 (4)
(4)
проведённый из положения которой занимала движущаяся м.т. в начальный момент некоторого промежутка времени, к положению, которой она занимает в конечный момент этого промежутка, называется перемещением. Перемещение является приращением радиус – вектора Dr.
При прямолинейном движении вектор перемещения совпадает с соответствующем участком траектории движения м.т. и модуль перемещения 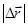 равен пройденному пути Ds,
равен пройденному пути Ds, 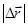 = Ds.
= Ds.
СКОРОСТЬ.
Движения очевидным образом различаются друг от друга тем, что тела могут проходить за одинаковые промежутки времени разные пути, или (говоря другими словами) тем, что одинаковые пути могут быть пройдены за различные промежутки времени. Эти различия в движении мы характеризуем, вводя понятие скорости.
Отношение вектора перемещения ко времени называется вектором средней скорости.
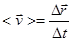 . (5)
. (5)
Направление вектора средней скорости совпадает с направлением вектора перемещения (рис. 3).
| |
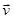
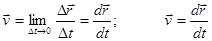 . (6)
. (6)
|

 Мгновенная скорость есть векторная величина, равная первой производной радиус – вектора движущейся материальной точки по времени. Так как секущая
Мгновенная скорость есть векторная величина, равная первой производной радиус – вектора движущейся материальной точки по времени. Так как секущая 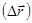 в пределе совпадает с касательной, то вектор мгновенной скорости
в пределе совпадает с касательной, то вектор мгновенной скорости 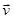 направлен по касательной к траектории в сторону движения (рис. 3). При Dt ® 0 путь Ds все больше приближается к
направлен по касательной к траектории в сторону движения (рис. 3). При Dt ® 0 путь Ds все больше приближается к 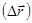 , поэтому величина мгновенной скорости
, поэтому величина мгновенной скорости
|
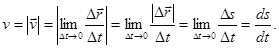
Т.о. величина (численное значение) мгновенной скорости равна первой производной пути во времени:
| |
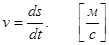 (7)
(7)
Т. о. численное значение скорости определяется как производная от пути по времени.
Проекции радиус – вектора 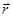 на оси координат x, y, z, поэтому проекции мгновенной скорости на эти оси равны первым производным от соответствующих координат движущейся м.т.:
на оси координат x, y, z, поэтому проекции мгновенной скорости на эти оси равны первым производным от соответствующих координат движущейся м.т.:
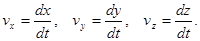
Величина полной мгновенной скорости
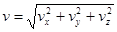 .
.
Вывод:скорость – физическая векторная величина, определяющая быстроту и направление движения.
Из формулы (7) получим выражение для пути, пройденного движущейся м.т. за отрезок времени 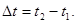
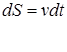 проинтегрируем данное выражение в интервале времени от t1 до t2
проинтегрируем данное выражение в интервале времени от t1 до t2
получим формулу позволяющую вычислить путь, пройденный телом за время 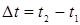 ,
,
если известна зависимость скорости от времени v(t):
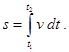 (8)
(8)
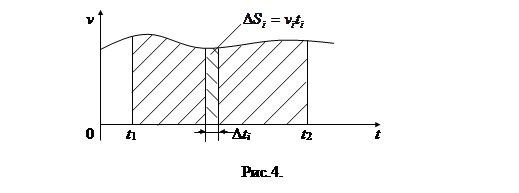
Геометрически смысл этой формулы ясен из рис. 4. По определению интеграла пройденный путь представляет собой площадь, ограниченную кривой v=v(t) в интервале от t1 до t2
 |
Движение называется равномерным, если величина скорости не меняется 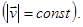
В случае равномерного движения уравнение (8) примет вид:
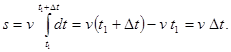
Обычно начальный момент времени 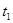 принимают за 0, тогда Dt = t - 0 = t, тогда
принимают за 0, тогда Dt = t - 0 = t, тогда
 s = v t путь пройденный телом при равномерном движении.
s = v t путь пройденный телом при равномерном движении.
УСКОРЕНИЕ.
В случае неравномерного прямолинейного движения изменяется величина скорости (v = v (t) ¹ const). А в случае криволинейного равномерного движения изменяется направление вектора скорости. Для характеристики того, насколько быстро со временем меняется скорость, вводится физическая величина, называемая ускорением.
Ускорение – физическая векторная величина, характеризующая быстроту изменения вектора скорости движения м.т. по числовому значению и по направлению.
Пусть скорость точки М1 в момент времени 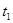 равна
равна 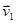 . За время Dt движущаяся м.т. перешла в положение М2 и приобрела скорость, отличную от
. За время Dt движущаяся м.т. перешла в положение М2 и приобрела скорость, отличную от 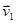 как по модулю так и по направлению, равную (рис. 5)
как по модулю так и по направлению, равную (рис. 5)
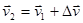 .
.
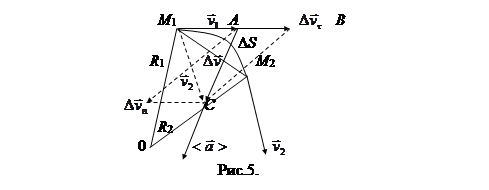
Для того, чтобы выразить изменение вектора скорости за интервал времени Dt, необходимо перенести вектор 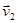 в точку М1 (параллельно самому себе) и найти разность векторов
в точку М1 (параллельно самому себе) и найти разность векторов
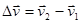 .
.
Средним ускорениемнеравномерного движения называется векторная величина, равная отношению изменения вектора скорости 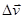 к интервалу времени Dt за которое произошло это изменение.
к интервалу времени Dt за которое произошло это изменение.
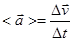 (9)
(9)
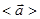 совпадает с направлением изменения быстроты скорости
совпадает с направлением изменения быстроты скорости 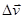 .
.
Мгновенным ускорением 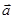 (ускорением) м.т. в момент времени t будет предел среднего ускорения
(ускорением) м.т. в момент времени t будет предел среднего ускорения
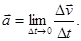
Таким образом, ускорение 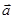 есть векторная величина равная первой производной скорости по времени или вторая производная радиус – вектор по времени
есть векторная величина равная первой производной скорости по времени или вторая производная радиус – вектор по времени
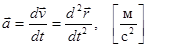
Разложим вектор 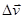 на две составляющие. Для этого из точки М1 по направлению
на две составляющие. Для этого из точки М1 по направлению 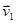 отложим вектор М1В по модулю равный
отложим вектор М1В по модулю равный 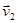 . Очевидно, что вектор АВ, равный
. Очевидно, что вектор АВ, равный 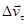 , представляет собой изменение скорости по модулю (числовому значению) за время Dt:
, представляет собой изменение скорости по модулю (числовому значению) за время Dt: 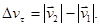 Вторая составляющая вектора
Вторая составляющая вектора 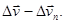 Она характеризует изменение скорости за время Dt по направлению.
Она характеризует изменение скорости за время Dt по направлению.
Ускорение (полное) при этом равно
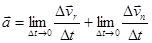
Таким образом, полное ускорение равно сумме двух слагаемых. Рассмотрим каждое из них в отдельности.
Предел отношения 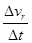 определяет быстроту изменения модуля скорости в данный момент времени t и называется касательным ( тангенциальным) ускорением ar.
определяет быстроту изменения модуля скорости в данный момент времени t и называется касательным ( тангенциальным) ускорением ar.
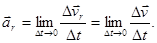
Касательное (тангенциальное) ускорение – составляющая полного ускорения движущейся м.т., направленная по касательной к её траектории и определяющее изменение величины скорости в единицу времени.
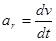 (11)
(11)
Вторая составляющая ускорения, равная 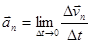 , называется нормальным(или центростремительным) ускорением и определяет быстроту изменения направления скорости.
, называется нормальным(или центростремительным) ускорением и определяет быстроту изменения направления скорости.
 Можно показать, что модуль нормального ускорения определяется выражением:
Можно показать, что модуль нормального ускорения определяется выражением:
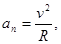 (12)
(12)
где R – радиус кривизны траектории.
При 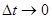 векторы
векторы 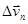 и
и 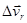 будут взаимно перпендикулярны и, следовательно, вектор
будут взаимно перпендикулярны и, следовательно, вектор 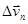 направлен по радиусу к центру кривизны траектории, а следовательно и
направлен по радиусу к центру кривизны траектории, а следовательно и 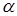 n .
n .
Полное ускорение тела – есть геометрическая сумма касательного и нормального ускорений (Рис.6).
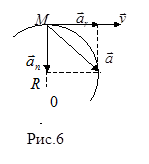
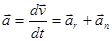
Модуль полного ускорения
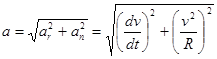
Рассмотрим частный случай.
1. 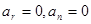 - прямолинейное равномерное движение.
- прямолинейное равномерное движение.
2. 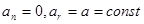 - прямолинейное равнопеременное движение. Скорость за равные промежутки времени меняется на равные величины. Тогда можно записать
- прямолинейное равнопеременное движение. Скорость за равные промежутки времени меняется на равные величины. Тогда можно записать
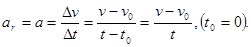
если начальный момент времени t0 = 0 и начальная скорость v0. Откуда конечная скорость.

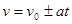 (13)
(13)
а > 0, если v > v0 - равноускоренное движение.
a < 0, если v < v0 – равнозамедленное движение.
Найдём формулу пути для равнопеременного движения. Из формул (8) и (13).
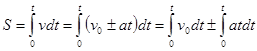

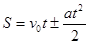 (14)
(14)
Можно показать:
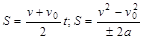
3. 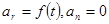 - прямолинейное движение с переменным ускорением.
- прямолинейное движение с переменным ускорением.
4. 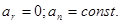 Из формулы
Из формулы 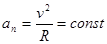 следует, что радиус кривизны должен быть постоянным (т.к. при
следует, что радиус кривизны должен быть постоянным (т.к. при 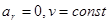 ). Следовательно, движение равномерное по окружности.
). Следовательно, движение равномерное по окружности.
5. 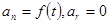 - равномерное криволинейное движение.
- равномерное криволинейное движение.
6. 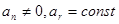 - криволинейное равнопеременное движение.
- криволинейное равнопеременное движение.
7. 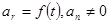 - криволинейное движение с переменным ускорением.
- криволинейное движение с переменным ускорением.

Еще одним примером равнопеременного движения может служить свободное падение тел у поверхности Земли с ускорением свободного падения g. В Севастополе g=9,807м/с2, оно зависит от широты, высоты над поверхностью планеты и на разных планетах принимает различные значения.
v=v0 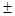 gt
gt
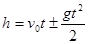 ;
; 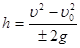 ;
; 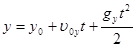 - уравнение движения.
- уравнение движения.
Дата добавления: 2020-10-01; просмотров: 223;