Горизонты энзимологии

В литературе появляются работы, в которых делаются попытки прогнозирования дальнейшего развития энзимологии на ближайшее десятилетие. Перечислим основные направления исследований энзимологии будущего. Во-первых, это исследования более тонких деталей молекулярного механизма и принципов действия ферментов в соответствии с законами классической органической химии и квантовой механики, а также разработка на этой основе теории ферментативного катализа. Во-вторых, это изучение ферментов на более высоких уровнях (надмолекулярном и клеточном) структурной организации живых систем, причем не столько отдельных ферментов, сколько ферментных комплексов в сложных системах. В-третьих, исследование механизмов регуляции активности и синтеза ферментов и вклада химической модификации в действие ферментов. В-четвертых, будут развиваться исследования в области создания искусственных низкомолекулярных ферментов – синзимов (синтетические аналоги ферментов), наделенных аналогично нативным ферментам высокой специфичностью действия и каталитической активностью, но лишенных побочных антигенных свойств. В-пятых, исследования в области инженерной энзимологии (белковая инженерия), создание «гибридных» катализаторов, сочетающих свойства ферментов, антител и рецепторов, а также создание биотехнологических реакторов с участием индивидуальных ферментов или полиферментных комплексов, обеспечивающих получение и производство наиболее ценных материалов и средств для народного хозяйства и медицины. Наконец, исследования в области медицинской энзимологии, основной целью которых является выяснение молекулярных основ наследственных и соматических болезней человека, в основе развития которых лежат дефекты синтеза ферментов или нарушения регуляции активности ферментов.

В природе существуют как простые, так и сложные ферменты. Первые целиком представлены полипептидными цепями и при гидролизе распадаются исключительно на аминокислоты. Такими ферментами (простые белки) являются гидролитические ферменты, в частности пепсин, трипсин, папаин, уреаза, лизоцим, рибонуклеаза, фосфатаза и др. Большинство природных ферментов относится к классу сложных белков, содержащих, помимо полипептидных цепей, какой-либо небелковый компонент (кофактор), присутствие которого является абсолютно необходимым для каталитической активности. Кофакторы могут иметь различную химическую природу и различаться по прочности связи с полипептидной цепью. Если константа диссоциации сложного фермента настолько мала, что в растворе все полипептидные цепи оказываются связанными со своими кофакторами и не разделяются при выделении и очистке, то такой фермент получает название холофермента (холоэнзим), а кофактор – простетической группы, рассматривающейся как интегральная часть молекулы фермента. Полипептидную часть фермента принято называть апоферментом.

В литературе до сих пор употребляются и другие наименования компонентов сложных ферментов, в частности «фермент-протеид», «белковый компонент» (апофермент), «кофермент» (коэнзим) и «простетическая группа». Под коферментом часто подразумевают дополнительную группу, легко отделяемую от апофермента при диссоциации. Предполагают, что простетическая группа может быть связана с белком ковалентными и нековалентными связями. Так, в молекуле ацетилкоэнзим-А-карбоксилазы кофактор биотин ковалентно связан с апоферментом посредством амидной связи. С другой стороны, химические связи между кофакторами и пептидными цепями могут быть относительно слабыми (например, водородные связи, электростатические взаимодействия и др.). В таких случаях при выделении ферментов наблюдается полная диссоциация обеих частей, и изолированый белковый компонент оказывается лишенным ферментативной активности, пока не будет добавлен извне недостающий кофактор. Именно к подобным изолированным низкомолекулярным органическим веществам применим термин «кофермент», типичными представителями которых являются витамины В₁, В₂, В₆, РР, содержащие кофер-менты. Известно также, что и простетические группы, и коферменты активно включаются в химические реакции, выполняя функции промежу-тоных переносчиков электронов, атомов водорода или различных функциональных групп (например, аминных, ацетильных, карбоксильных). В подобных случаях кофермент рассматривают в качестве второго субстрата, или косубстрата.

Субстрат подвергается окислению, отдавая электроны и протоны, а КоЕ – восстановлению, принимая электроны и протоны. В следующей полуреакции восстановленный КоЕН может отдавать электроны и протоны на какой-либо другой промежуточный переносчик электронов и протонов или на конечный акцептор.

Роль кофермента (Ко) в качестве переносчика, например, атомов водорода может быть представлена в виде схемы:

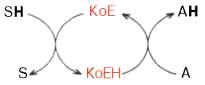
где SH – субстрат; КоЕ – холофермент; А – акцептор протона.

Рисунок 33 - Перенос атомов водорода

Коэнзим, кофактор, простетическая группа – двусмысленный биохимический жаргон. До сих пор продолжается терминологический спор, поскольку часто определения «коэнзим», «кофактор» и «простетическая группа» рассматриваются через призму их роли в реакциях энзиматического (ферментативного) катализа. Следует, однако, считаться с тем неоспоримым фактом, что во многих случаях небелковые органические молекулы, как и ионы металлов, абсолютно необходимы белковому компоненту при выполнении определенной биологической функции, не имеющей отношения к биокатализу. Несомненно, имеют значение также тип и характер связи небелкового компонента с молекулой белка. Поэтому очевидно, что кофактором может служить любой фактор, абсолютно необходимый для выполнения белком его каталитической или любой другой биологической роли. С другой стороны, коферментом может быть любой небелковый фактор, который непосредственно вовлечен в реакцию энзиматического катализа. Кофактор, который непосредственно не участвует в акте катализа, не является коэнзимом. В то же время простетическую группу (ковалентно связанный небелковый компонент, необходимый для определенной функции) можно назвать коферментом, если она непосредственно участвует в энзиматической реакции. Простетическая группа, которая не вовлечена в акт катализа, но функционально является существенным как для фермента, так и для некаталитического белка, может быть названа кофактором. И наконец, кофактор и кофермент, непрочно связанные (или слабо связанные) с ферментом или белком, тем не менее не классифицируются в качестве простетических групп.

Многие двухвалентные металлы (Mg²⁺, Мn²⁺, Са²⁺), как будет показано далее, также выполняют роль кофакторов, хотя они не относятся ни к коферментам, ни к простетическим группам. Известны примеры, когда ионы металлов прочно связаны с белковой молекулой, выполняя функции простетической группы. В частности, очищенный фермент, катализирующий окисление аскорбиновой кислоты (витамин С) в дезоксиаскорбиновую кислоту, содержит 8 атомов меди на одну молекулу; все они настолько прочно связаны с белковой молекулой, что даже не обмениваются с ионообменными смолами и не отделяются методом диализа. Более того, с помощью метода электронного парамагнитного резонанса показано участие ионов меди в промежуточном переносе электронов. Интересно отметить, что свободные ионы меди также наделены каталитической активностью при окислении аскорбиновой кислоты, однако эта активность повышается во многие тысячи раз, если ионы меди соединяются с апоферментом в единый комплекс – холофермент.

Получены доказательства кофакторной функции в ферментативных реакциях и ряда других биологически активных соединений, не относящихся к витаминам: HS-глутатиона, АТФ, липоевой кислоты, производных ну-клеозидов (уридинфосфат, цитидинфосфат, фосфоаденозинфосфосульфат), порфиринсодержащих веществ и др. Сюда же могут быть отнесены тРНК, которые в составе ферментов аминоацил-тРНК-синтетаз принимают активное участие в транспорте аминокислот в рибосоме, где осуществляется синтез белка.

Следует отметить одну отличительную особенность двухкомпонентных ферментов: ни кофактор отдельно (включая большинство коферментов), ни сам по себе апофермент каталитической активностью не наделены, и только их объединение в одно целое, протекающее не хаотично, а в соответствии с программой их структурной организации, обеспечивает быстрое протекание химической реакции.

При изучении механизма химической реакции, катализируемой ферментами, исследователя всегда интересует не только определение промежуточных и конечных продуктов и выяснение отдельных стадий реакции, но и природа тех функциональных групп в молекуле фермента, которые обеспечивают специфичность действия фермента на данный субстрат (субстраты) и высокую каталитическую активность. Речь идет, следовательно, о точном знании геометрии и третичной структуры фермента, а также химической природы того участка (участков) молекулы фермента, который обеспечивает высокую скорость каталитической реакции. Участвующие в ферментативных реакциях молекулы субстратов часто имеют небольшие размеры по сравнению с молекулами ферментов, поэтому было высказано предположение, что при образовании фермент-субстратных комплексов в непосредственный контакт с молекулой субстрата, очевидно, вступает ограниченная часть аминокислот пептидной цепи. Отсюда возникло представление об активном центре фермента. Под активным центром подразумевают уникальную комбинацию аминокислотных остатков в молекуле фермента, обеспечивающую непосредственное связывание ее с молекулой субстрата и прямое участие в акте катализа. Установлено, что у сложных ферментов в состав активного центра входят также простетические группы.

В активном центре условно различают так называемый каталитический центр, непосредственно вступающий в химическое взаимодействие с субстратом, и связывающий центр, или контактную («якорную») площадку, которая обеспечивает специфическое сродство к субстрату и формирование его комплекса с ферментом (см. рисунок 34, 35). В свою очередь молекула субстрата также содержит функционально различные участки: например, субстраты эстераз или протеиназ – одну специфическую связь (или группу атомов), подвергающуюся атаке со стороны фермента, и один или несколько участков, избирательно связываемых ферментом.

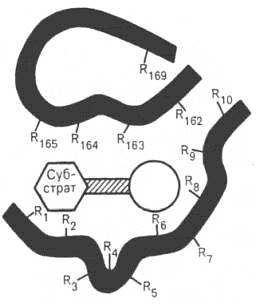
Темные полосы - участки полипептидной цепи фермента; R - аминокислотные остатки и их порядковые номера (с N-конца).

Рисунок 34 - Активный центр фермента в структурной модели

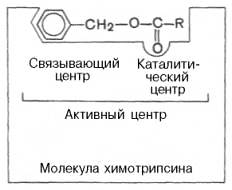
Рисунок 35 - Активный центр фермента (схема) (по Малеру и Кордесу)

Получены экспериментальные доказательства наличия в активном центре химотрипсина двух остатков гистидина и остатка серина, схематически представленных в трехмерной структурной модели предшественника этого фермента (см. рисунок 36). Выявление химической природы и вероятной топографии групп активного центра – проблема первостепенной важности. Она сводится к определению природы аминокислот, их последовательности и взаиморасположения в активном центре. Для идентификации так называемых существенных аминокислотных остатков используют специфические ингибиторы ферментов (часто это субстрат подобные вещества или аналоги коферментов), методы «мягкого» (ограниченного) гидролиза в сочетании с химической модификацией, включающей избирательное окисление, связывание, замещение остатков аминокислот и др.

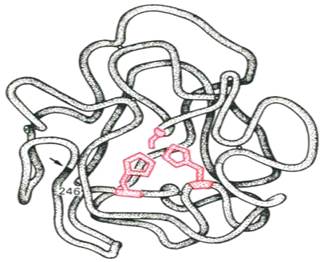
Рисунок 36 - Гипотетическая модель третичной структуры молекулы предшественника химотрипсина (по Нейрату). Цветом выделены остатки серина и гистидина; стрелкой обозначено место отщепления N-концевого участка полипептидной цепи

При помощи методов ингибиторного анализа были предприняты попытки установить закономерности состава и структуры активных центров у ферментов, относящихся к разным группам. В частности, при использовании диизопропилфторфосфата (ДФФ), принадлежащего к так называемым нервным ядам, наблюдается полное выключение активного центра холинэстеразы – фермента, катализирующего гидролиз ацетилхолина на холин и уксусную кислоту. Оказалось, что этот ингибитор имеет близкое структурное сходство с ацетилхолином и подобно ему взаимодействует с ОН-группой остатка серина в активном центре. Вызывая фосфорилирование серина в активном центре ряда других ферментов, ДФФ также инактивирует их действие (см. рисунок 37):

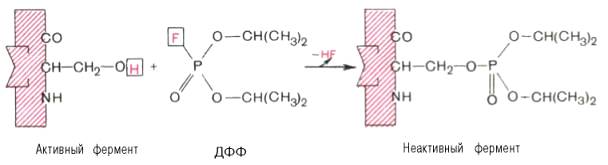
Рисунок 37 - Инактивация фермента диизопропилфторфосфатом (схема)

Показано, что ДФФ избирательно фосфорилирует в каждом чувствительном к нему ферменте только один остаток серина, наделенный функциональной активностью. Учитывая этот механизм действия ДФФ, сделаны попытки определения природы аминокислот в окружении «каталитического» остатка серина у ряда ферментов.

Существенное значение ОН-группы серина для акта катализа было доказано, химическим ее блокированием или удалением, когда эстеразы полностью лишались ферментативной активности.

Предполагают, что формирование активного центра фермента начинается уже на ранних этапах синтеза белка-фермента на рибосоме, когда линейная одномерная структура пептидной цепи превращается в трехмерное тело строго определенной конфигурации. Образовавшийся белок приобретает информацию совершенно нового типа, а именно функциональную (в частности, каталитическую). Любые воздействия, приводящие к денатурации, т.е. нарушению третичной структуры, приводят к искажению или разрушению структуры активного центра и соответственно потере ферментом каталитических свойств. Если при подходящих внешних условиях удается восстановить нативную трехмерную структуру белка-фермента (ренатурировать его), то восстанавливается и его каталитическая активность. Это было показано впервые на примере рибонуклеазы поджелудочной железы.

Помимо активного центра, в молекуле фермента может присутствовать также аллостерический центр (или центры) (от греч. allos – другой, иной и steros – пространственный, структурный), представляющий собой участок молекулы фермента, с которым связываются определенные, обычно низкомолекулярные, вещества (эффекторы, или модификаторы), молекулы которых отличаются по структуре от субстратов. Присоединение эффектора к аллостерическому центру изменяет третичную и часто также четвертичную структуру молекулы фермента и соответственно конфигурацию активного центра, вызывая снижение или повышение энзиматической активности. Ферменты, активность каталитического центра которых подвергается изменению под влиянием аллостерических эффекторов, связывающихся с аллостерическим центром, получили название аллостерических ферментов (см. рисунок 18):

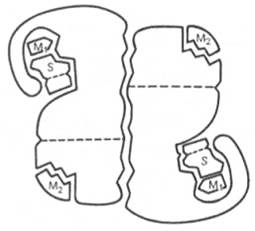
S – субстрат; М₁ – модификатор, связывающийся в активном центре; М₂ – модификатор, связывающийся в аллостерическом центре (эффектор).

Рисунок 38 -Схематическое изображение аллостерического фермента, состоящего из двух протомеров, соединенных по типу гетерологической («голова»-«хвост») ассоциации (по Кошленду)

Отличительной особенностью ряда аллостерических ферментов является наличие в молекуле олигомерного фермента нескольких активных центров и нескольких аллостерических регуляторных центров, пространственно удаленных друг от друга. В аллостерическом ферменте каждый из двух симметрично построенных протомеров содержит один активный центр, связывающий субстрат S, и один аллостерический центр, связывающий эффектор М₂, т.е. 2 центра в одной молекуле фермента. Получены доказательства, что для субстрата аллостерические ферменты, помимо активного центра, содержат и так называемые эффекторные центры; при связывании с эффекторным центром субстрат не подвергается каталитическому превращению, однако он влияет на каталитическую эффективность активного центра. Подобные взаимодействия между центрами, связывающими лиганды одного типа, принято называть гомотропными взаимодействиями, а взаимодействия между центрами, связывающими лиганды разных типов, – гетеротропными взаимодействиями.

Таким образом, приведенные сведения о химической природе активного центра и аллостерических участках свидетельствуют о том, что в энзиматическом катализе, как и в реакции связывания субстрата, участвует не ограниченная и небольшая часть фермента, как предполагалось ранее, а значительно большая часть молекулы белка-фермента. Этими обстоятельствами, вероятнее всего, можно объяснить большие размеры и объемность трехмерной структуры молекулы фермента; эти же обстоятельства следует учитывать в программах создания искусственных низкомолекулярных аналогов ферментов (синзимов), обладающих свойствами нативных ферментов.

Структура и функции ферментов, а также механизм их действия почти ежегодно подробно обсуждаются на многих международных симпозиумах и конгрессах. Важное место отводится рассмотрению структуры всей молекулы фермента и ее активных центров, молекулярному механизму действия различных типов ферментов, общей теории энзиматического катализа. Тем не менее до сих пор нет полной ясности по двум кардинальным проблемам энзимологии: чем вызваны специфичность действия и высокая каталитическая эффективность ферментов?

До установления химической природы ферментов гипотезы о механизме их действия опирались на исследования кинетики и модельные опыты химического гомогенного катализа. Повышение скорости химических реакций под действием ферментов объясняли следующим: а) активированием субстрата в результате образования адсорбционных или молекулярных, обратимо диссоциирующих фермент-субстратных комплексов; б) цепным механизмом реакций с участием радикалов или возбужденных молекул. Оказалось, что цепные механизмы реакции не играют существенной роли в биологическом катализе. После установления химической природы ферментов подтвердилось представление, выдвинутое более 80 лет назад В. Анри, Л. Михаэлисом и М. Ментен, о том, что при энзиматическом катализе фермент Е соединяется (в принципе обратимо) со своим субстратом S, образуя нестойкий промежуточный фермент-субстратный комплекс ES, который в конце реакции распадается с освобождением фермента и продуктов реакции Р. Благодаря высокому сродству связывания и образованию ES-комплекса резко возрастает число молекул субстрата, вступающих в реакции. Эти представления легли в основу теории «ключа-замка» Э. Фишера, которую иногда называют теорией «жесткой матрицы». Таким образом, жесткая структура активного центра оказывается комплементарной молекулярной структуре субстрата, обеспечивая тем самым высокую специфичность фермента.

Л. Михаэлис не только постулировал образование промежуточного фермент-субстратного ES-комплекса, но и рассчитал влияние концентрации субстрата на скорость реакции. В процессе реакции различают несколько стадий: присоединение молекулы субстрата к ферменту, преобразование первичного промежуточного соединения в один или несколько последовательных (переходных) комплексов и протекающее в одну или несколько стадий отделение конечных продуктов реакции от фермента. Это можно схематически проиллюстрировать следующими примерами (5):

E+S↔ES→…→E+P (5)

В реакциях анаболизма, например, А + В —> АВ, фермент может соединяться как с одним, так и с другим субстратом или обоими субстратами (см. рисунок 39)

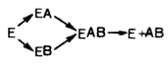
Рисунок 39 – Реакции анаболизма (схема)

В реакциях катаболизма (см. рисунок 40), например АВ —> А + В:

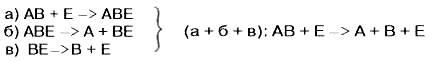
Рисунок 40 – Реакции катаболизма

Фермент вступает во взаимодействие с субстратом на очень короткий период, поэтому долгое время не удавалось показать образование такого комплекса. Прямые доказательства существования фермент-субстратного комплекса были получены в лабораториях Д. Кейлина и Б. Чанса. В настоящее время экспериментальные и математические методы кинетики, термодинамики и статической механики химических реакций позволяют (см. рисунок 41):

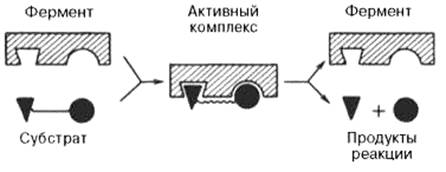
Рисунок 41 -Образование нестойкого фермент-субстратного комплекса согласно теории Э. Фишера «ключ-замок»

Определить для ряда ферментативных реакций кинетические и термодинамические показатели, в частности константы диссоциации промежуточных фермент-субстратных комплексов, константы скорости и равновесия их образования (см. рисунок 42).

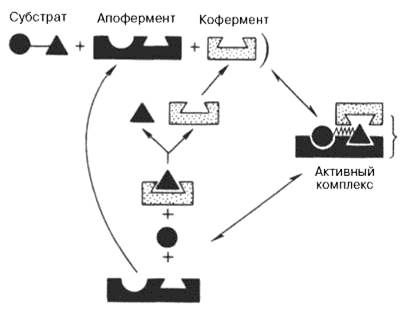
Рисунок 42 -Функция кофермента (по А. Кантарову и Б. Шепартцу)

В образовании фермент-субстратных комплексов участвуют водородные связи, электростатические и гидрофобные взаимодействия, а в ряде случаев также ковалентные, координационные связи. Информация о природе связей между субстратом и связывающим участком активного центра фермента может быть получена методами ЭПР и ЯМР, а также методами УФ- и ИК-спектроскопии (см. рисунок 43):

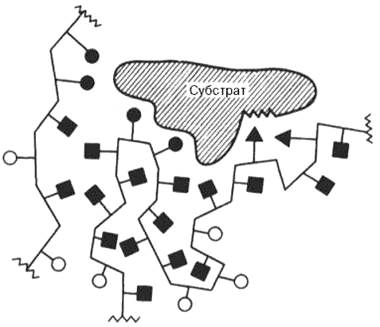
Рисунок 43 -Образование нековалентных связей между ферментом и субстратом (схема)

Для каталитической активности фермента существенное значение имеет пространственная структура, в которой жесткие участки α-спиралей чередуются с гибкими, эластичными линейными отрезками, обеспечивающими динамические изменения белковой молекулы фермента. Этим изменениям придается большое значение в некоторых теориях ферментативного катализа. Так, в противоположность модели Э. Фишера «ключ-замок» Д. Кошлендом была разработана теория «индуцированного соответствия», допускающая высокую конформационную лабильность молекулы белка-фермента и гибкость и подвижность активного центра. Эта теория была основана на весьма убедительных экспериментах, свидетельствующих о том, что субстрат индуцирует конформационные изменения молекулы фермента таким образом, что активный центр принимает необходимую для связывания субстрата пространственную ориентацию. Иными словами, фермент только в присутствии (точнее, в момент присоединения) субстрата будет находиться в активной (напряженной) Т-форме в отличие от неактивной R-формы (см. рисунок 44). На рисунке 44 видно, что присоединение субстрата S к ферменту Е, вызывая соответствующие изменения конформации активного центра, в одних случаях приводит к образованию активного комплекса, в других – неактивного комплекса вследствие нарушения пространственного расположения функциональных групп активного центра в промежуточном комплексе.

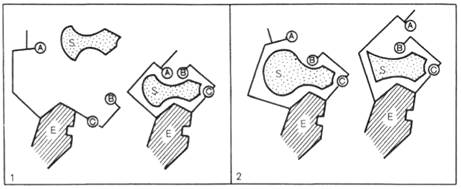
А, В, С - функциональные группы активного центра; 1 - активный комплекс; 2 - неактивный комплекс.

Рисунок 44 -Изменения структуры активного центра фермента, вызванные субстратом, согласно модели «индуцированного соответствия» Д. Кошленда

Получены экспериментальные доказательства нового положения о том, что постулированное Д. Кошлендом «индуцированное соответствие» субстрата и фермента создается не обязательно изменениями конформации белковой молекулы, но также геометрической и электронно-топографической перестройкой молекулы субстрата.

В каталитическом процессе существенное значение имеют точное соответствие между ферментом и субстратом, а также термодинамические и каталитические преимущества подобного соответствия. Гипотеза «индуцированного соответствия» предполагает существование между ферментом и субстратом не только пространственной или геометрической компле-ментарности, но и электростатического соответствия, обусловленного спариванием противоположно заряженных групп субстрата и активного центра фермента. Точное соответствие обеспечивает образование эффективного комплекса между субстратом и ферментом.

Подобно другим катализаторам, ферменты, с термодинамической точки зрения, ускоряют химические реакции за счет снижения энергии активации. Энергией активации называется энергия, необходимая для перевода всех молекул моля вещества в активированное состояние при данной температуре. Другими словами, это энергия, необходимая для запуска химической реакции, без которой реакция не начинается несмотря на ее термодинамическую вероятность. Фермент снижает энергию активации путем увеличения числа активированных молекул, которые становятся реакционно-способными на более низком энергетическом уровне (см. рисунок 45)

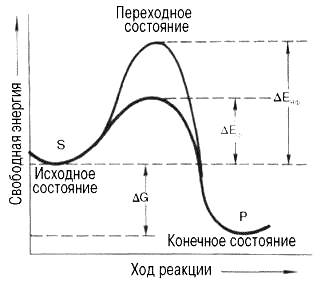
S – исходный субстрат; Р - продукт; ΔЕ_НФ -энергия активации неферментативной реакции; ΔЕ_Ф - энергия активации ферментативной реакции; ΔG - стандартное изменение свободной энергии.

Рисунок 45 -Энергетический механизм ферментативной и неферментативной химических реакций

На рисунке 45 видно, что ферментативная реакция имеет более низкую энергию активации. Следует отметить, что как катализируемая ферментом, так и не катализируемая им реакция независимо от ее пути имеет одинаковую величину стандартного изменения свободной энергии (ΔG). Действуя на скорость реакции, ферменты не изменяют равновесия между прямой и обратной реакциями, как и не влияют на величину свободной энергии реакции; они лишь ускоряют наступление равновесия химической реакции.

Зависимость между константой равновесия и изменением свободной энергии реагирующих веществ математически принято выражать уравнением (6):

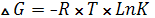, (6)

где R – газовая постоянная;

Т – абсолютная температура в Кельвинах;

lnК – натуральный логарифм константы равновесия;

ΔG – стандартное изменение свободной энергии, Дж/моль.

Из представленного уравнения вытекает, что при высоком значении К величина ΔG оказывается отрицательной. Подобные реакции сопровождаются уменьшением свободной энергии. При низком значении К величина ΔG оказывается положительной. Если константа равновесия равна единице, то изменение свободной энергии будет равно нулю и реакция легко обратима.

Для измерения константы равновесия и величины свободной энергии какой-либо химической реакции, например реакции взаимопревращения глюкозо-1-фосфата в глюкозо-6-фосфат, катализируемой ферментом фосфоглюкомутазой, определяют количество глюкозо-6- и глюкозо-1-фосфата при достижении химического равновесия. В состоянии равновесия содержание глюкозо-6-фосфата оказывается в 19 раз больше количества глюкозо-1-фосфата. Отсюда константа равновесия К равна 19. Подставляя эту цифру в уравнение, получаем ΔG = –7329 Дж/моль. Это означает, что при превращении 1 моля глюкозо-1-фосфата в 1 моль глюкозо-6-фосфата при температуре 25 °С происходит уменьшение свободной энергии системы на 7329 Дж.

Таким образом, в механизме ферментативного катализа ведущую роль играют промежуточные фермент-субстратные комплексы, образование которых определяется как тонкой трехмерной структурой активного центра, так и уникальной структурной организацией всей молекулы фермента, обеспечивающими высокую каталитическую активность и специфичность действия биокатализатора.

Одним из характерных проявлений жизни является удивительная способность живых организмов кинетически регулировать химические реакции, подавляя стремление к достижению термодинамического равновесия. Ферментативная кинетика занимается исследованием закономерностей влияния химической природы реагирующих веществ (ферментов, субстратов) и условий их взаимодействия (концентрация, рН среды, температуры, присутствие активаторов или ингибиторов) на скорость ферментативной реакции. Главной целью изучения кинетики ферментативных реакций является получение информации, которая может способствовать выяснению молекулярного механизма действия фермента.

Общие принципы кинетики химических реакций применимы и к ферментативным реакциям. Известно, что любая химическая реакция характеризуется константой термодинамического равновесия предсатвленной системой (7). Она выражает состояние химического равновесия, достигаемого системой, и обозначается К_р:

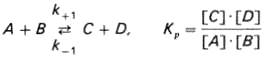(7)

Константа равновесия равна произведению концентраций образующихся веществ, деленному на произведение концентрации исходных веществ. Значение константы равновесия обычно находят из соотношения констант скоростей прямой (k₊₁) и обратной (k _–1) реакций, т.е. К_p = k₊₁/k_–1.

В состоянии равновесия скорость прямой реакции: v₊₁ = k _{+ 1}[ А ] • [ B ] равна скорости обратной реакции: v_–1=k_–1[С] • [D], т. е. v₊₁= v_–1 соответственно k₊₁[А]•[B] = k_–1[С]•[D], или (см. рисунок 46)

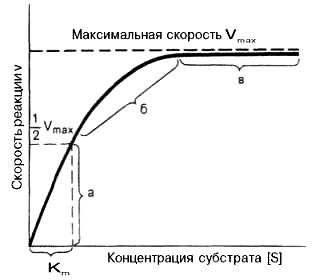
а - реакция первого порядка (при [S]<К_m скорость реакции пропорциональна концентрации субстрата); б - реакция смешанного порядка; в – реакция нулевого порядка, когда v = V_maxи скорость реакции не зависит от концентрации субстрата.

Рисунок 46 -Теоретический график зависимости скорости ферментативной реакции от концентрации субстрата при постоянной концентрации фермента

Таким образом, константа равновесия равна отношению констант скоростей прямой и обратной реакций (8). Величину, обратную константе равновесия, принято называть субстратной константой, или, в случае ферментативной реакции, константой диссоциации фермент–субстратного комплекса, и обозначать символом K_S:

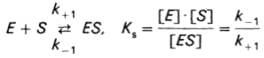(8)

т.е. K_S равна отношению произведения концентрации фермента и субстрата к концентрации фермент-субстратного комплекса или отношению констант скоростей обратной и прямой реакций. Следует отметить, что константа K_S зависит от химической природы субстрата и фермента и определяет степень их сродства. Чем ниже значение K_S, тем выше сродство фермента к субстрату.

При изучении кинетики ферментативных реакций следует учитывать одну важную особенность этих реакций (не свойственную обычным химическим реакциям), связанную с явлением насыщения фермента субстратом. При низкой концентрации субстрата зависимость скорости реакции от концентрации субстрата является почти линейной и подчиняется кинетике первого порядка. Это означает, что скорость реакции S —> Р прямо пропорциональна концентрации субстрата S и в любой момент времени t определяется следующим кинетическим уравнением 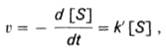(9):

(9)

где [S] – молярная концентрация субстрата S;

d[S]/dt – скорость убыли субстрата;

k' – константа скорости реакции, которая в данном случае имеет размерность, обратную единице времени (мин^–1 или с^–1).

При высокой концентрации субстрата скорость реакции максимальна, становится постоянной и не зависящей от концентрации субстрата [S] . В этом случае реакция подчиняется кинетике нулевого порядка v = k" (при полном насыщении фермента субстратом) и целиком определяется концентрацией фермента. Различают, кроме того, реакции второго порядка, скорость которых пропорциональна произведению концентраций двух реагирующих веществ. В определенных условиях при нарушении пропорциональности говорят иногда о реакциях смешанного порядка.

Изучая явление насыщения, Л. Михаэлис и М. Ментен разработали общую теорию ферментативной кинетики. Они исходили из предположения, что ферментативный процесс протекает в виде следующей химической реакции 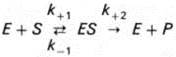(10):

(10)

т.е. фермент Е вступает во взаимодействие с субстратом S с образованием промежуточного комплекса ES, который далее распадается на свободный фермент и продукт реакции Р. Математическая обработка на основе закона действующих масс дала возможность вывести уравнение, названное в честь авторов уравнением Михаэлиса–Ментен (11), выражающее количественное соотношение между концентрацией субстрата и скоростью ферментативной реакции:

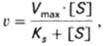(11)

где v – наблюдаемая скорость реакции при данной концентрации субстрата [S];

K_S– константа диссоциации фермент-субстратного комплекса, моль/л;

V_max– максимальная скорость реакции при полном насыщении фермента субстратом.

Из уравнения Михаэлиса–Ментен следует, что при высокой концентрации субстрата и низком значении K_S скорость реакции является максимальной, т.е. v = V_max(реакция нулевого порядка). При низкой концентрации субстрата, напротив, скорость реакции оказывается пропорциональной концентрации субстрата в каждый данный момент (реакция первого порядка).

Следует указать, что уравнение Михаэлиса–Ментен в его классическом виде не учитывает влияние на скорость ферментативного процесса продуктов реакции, и носит несколько ограниченный характер. Поэтому были предприняты попытки усовершенствовать его. Так, было предложено уравнение Бриггса-Холдейна 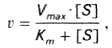(12):

(12)

где К_m представляет собой константу Михаэлиса, являющуюся экспериментально определяемой величиной. Она может быть представлена следующим уравнением 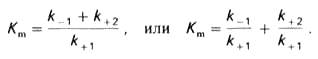(13):

(13)

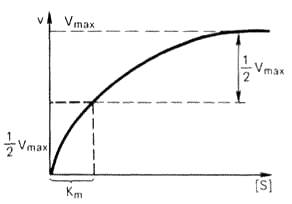
Рисунок 47 -Кривая уравнения Михаэлиса-Ментен: гиперболическая зависимость начальных скоростей катализируемой ферментом реакции от концентрации субстрата

В числителе представлены константы скоростей распада комплекса ES в двух направлениях (в сторону исходных Е и S и в сторону конечных продуктов реакции Е и Р). Отношение k_–1/k₊₁представляет собой константу диссоциации фермент субстратного комплекса K_S, тогда 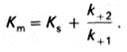(14):

(14)

Отсюда вытекает важное следствие: константа Михаэлиса всегда больше константы диссоциации фермент-субстратного комплекса K_S на величину (15):

k₊₂/k₊₁ (15)

Для определения численного значения К_m обычно находят ту концентрацию субстрата, при которой скорость ферментативной реакции v составляет половину от максимальной V_max, т.е. если v = ^½ V_maх. Подставляя значение v в уравнение Бриггса–Холдейна, получаем 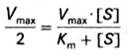(16):

(16)

разделив обе части уравнения на V_mах, получим 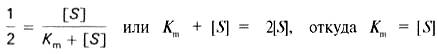(17)

(17)

Таким образом, константа Михаэлиса численно равна концентрации субстрата (моль/л), при которой скорость данной ферментативной реакции составляет половину от максимальной.

Определение величины К_m имеет важное значение при выяснении механизма действия эффекторов на активность ферментов и т.д. Константу Михаэлиса можно вычислить по графику. Отрезок на абсциссе, соответствующий скорости, равной половине максимальной, будет представлять собой К_m.

Пользоваться графиком, построенным в прямых координатах зависимости начальной скорости реакции v₀ от начальной концентрации субстрата [S₀], неудобно, поскольку максимальная скорость V_max является в данном случае асимптотической величиной и определяется недостаточно точно.

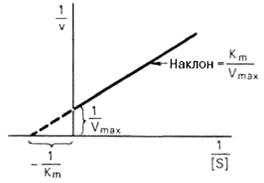
Рисунок 45 -График Лайнуивера-Бэрка

Для более удобного графического представления экспериментальных данных Г. Лайнуивер и Д. Бэрк преобразовали уравнение Бриггса–Хол-дейна по методу двойных обратных величин исходя из того принципа, что если существует равенство между двумя какими-либо величинами, то и обратные величины также будут равны 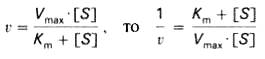(18):

(18)

Или 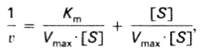(19)

(19)

то после преобразования получаем уравнение 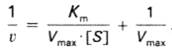(20):

(20)

которое получило назва<