Простейшие виды нагружения и простейшие конструктивные элементы
Для отдельно взятого элемента конструкции взаимоуравновешенные активная сила и сила реакции опоры являются внешними силами.
Рассмотрим, каким образом конструкция оказывает сопротивление внешней нагрузке, за счет чего происходит изменение формы и размеров конструкции -деформирование(от лат. deformatio - искажение).
Растяжение
Не обращая внимание на то, каким образом, с точки зрения конструктивного решения, приложены внешние силы Р, рассмотрим растяжение элемента конструкции, схема нагружения которого показана на рис. 10.3,а. На рис. 10.3 показана также упрощенная
|
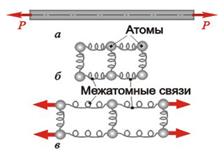
| Рис. 10.3. Упрощенная модель деформации при растяжении |
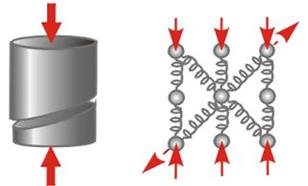
модель межатомных связей в твердом теле. Жесткие и прочные межатомные связи, соединяющие атомы недеформированного тела (рис. 10.3,б), при растяжении (рис. 10.3,в) создают большие внутренние силы противодействия внешней нагрузке, стремящиеся сохранить тело как единое целое.
Под действием внешних сил частицы (атомы) материала, из которого сделана конструкция, будут перемещаться, и перемещение частиц под нагрузкой будет продолжаться, пока между внешними и внутренними силами не установится равновесие.
Такое состояние называется деформированным состоянием тела.
Мерой воздействия внешних сил на атомы вещества, которые удаляются друг от друга (при растяжении) или сближаются (при сжатии), т. е. мерой противодействия материала конструкции внешнему силовому воздействию, мерой внутренних сил в материале является напряжение. Напряжением называется внутренняя сила (возникающая при воздействии внешней нагрузки), приходящаяся на единицу площади в окрестности данной точки рассматриваемого сечения тела:
σ = Р/F,
| где | σ | - | напряжение, Па (1Па=1Н/м2); | |
| P | - | суммарная сила, Н; | ||
| F | - | площадь поперечного сечения, перпендикулярного направлению действующей силы P,м2. |
В инженерной практике иногда измеряют напряжения в даН/мм2 (1даН=10Н).
Напряжение, таким образом, показывает интенсивность противодействия внутренних сил воздействию внешней нагрузки на межатомные связи материала конструкции, или, что то же самое, интенсивность воздействия внешней нагрузки на межатомные связи.
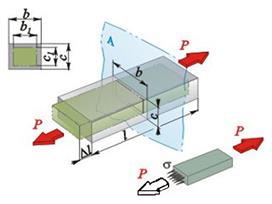
Если рассмотреть деформированное состояние стержня (бруса) (рис. 10.4) при растяжении внешними силами Р (показаны на рисунке черными стрелками), то в любом произвольно взятом поперечном сечении (например, плоскостью А) распределение нормальных напряжений σ = Р/F будет равномерным.
|
| Рис. 10.4. Деформированное состояние бруса |
Равнодействующая сила напряжений σ - внутренняя сила Р = σF (на рис. 10.4 - белая стрелка) - проходит через центр тяжести поперечного сечения вдоль линии действия внешней силы и равна ей.
Под действием растягивающих сил Р длина стержня l увеличивается на величину Δl, называемуюабсолютным удлинением. Растяжение сопровождается также уменьшением поперечных размеров сечения. Это явление носит название "эффект Пуассона" (по имени французского ученого и механика С. Пуассона). Абсолютное поперечное сужение стержня при растяжении Δb = b - b1; Δc = c - c1.
Именно за счет изменения формы и размеров любая конструкция сопротивляется (создает силы противодействия) внешним нагрузкам.
В инженерной практике деформированное состояние принято оценивать не только абсолютными величинами изменений формы ("перемещениями"), но и относительными безразмерными величинами - "деформациями":
ε = Δl/l; 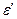 = Δb/b = Δc/c,
= Δb/b = Δc/c,
| где | ε | - | относительное удлинение при растяжении; | |
| ε' | - | относительные поперечные деформации. |
При достаточно больших внешних нагрузках (и, как следствие, больших внутренних напряжениях) межатомные связи материала могут быть разорваны, что приведет к разрушению конструкции.
Конструкция должна быть спроектирована так, чтобы она не разрушилась под нагрузкой. Деформации (перемещения), которые неизбежно возникают в конструкции под нагрузкой, должны быть вполне определенными и достаточно малыми, поскольку выбранные размеры и форма элементов конструкции обеспечивают определенное качество ее функционирования.
Так, изменение под нагрузкой размеров и формы элементов конструкции самолета, обтекаемых потоком воздуха, существенным образом влияет на аэродинамические характеристики и, как следствие, - на летно-технические характеристики самолета.
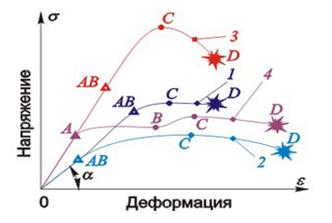
Характер работы конструкции под нагрузкой во многом определяется выбором конструкционных материалов. Одной из основных характеристик материала конструкции являетсядиаграмма растяжения (кривая деформирования) - взаимозависимость напряжений и деформаций удлинения, получаемая в результате испытаний образцов материалов на растяжение. На рис. 10.5 показан типичный характер диаграмм растяжения для некоторых конструкционных материалов, применяемых в самолетостроении.
|
| Рис. 10.5. Диаграмма растяжения: 1 - высокопрочные алюминиевые сплавы; 2 - пластичные алюминиевые сплавы; 3 - высокопрочные легированные стали; 4 - малоуглеродистые стали |
Прямолинейные на некотором протяжении диаграммы участки (0-А, 0-АВ) характеризуют такую стадию деформирования образца, когда при увеличении нагрузки деформации пропорциональны напряжениям и при снятии нагрузки исчезают, т. е. образец за счет межатомных связей (сил упругости) возвращается в исходное (недеформированное) состояние. На этом участке материал "подчиняется" закону Гука (по имени английского естествоиспытателя Р. Гука):
σ = Еε,
| где | σ | - | напряжение, Па; | |
| E | - | модуль упругости материала, или модуль Юнга (по имени английского ученого Т.Юнга), Па; | ||
| ε | - | относительное удлинение. |
Модуль упругости Е (наклон кривой деформирования в зоне упругости 0-А (0-АВ) диаграммы: Е = tgα) является мерой упругости ("жесткости") и характеризует податливость (способность к деформированию) под нагрузкой. Отметим, что сталь - более жесткий, менее податливый материал, чем алюминиевый сплав.
Точка А (АВ) на диаграммах характеризует наибольшую нагрузку Рпц и, соответственно, напряженияпредела пропорциональности σпц, при которых еще соблюдается линейная зависимость σ - ε.
Дальше, за точкой А (АВ), линейная зависимость σ - ε нарушается, материал деформируется ("течет") под нагрузкой и при снятии нагрузки не возвращается к исходному состоянию, в нем возникают остаточные пластические деформации за счет того, что часть межатомных связей разрушается. Точка В на диаграммах характеризует нагрузку Рт и, соответственно,напряженияпредела текучести σт, при которых материал "течет" без увеличения нагрузки. Некоторые материалы (например, 4, см. рис. 10.5) имеют явно выраженную площадку текучести А-В, где деформации существенно увеличиваются без увеличения внешней нагрузки. Для других материалов (1, 2, 3) площадки текучести отсутствуют, в этом случае точки А и В на диаграмме практически совпадают.
Зона В-С диаграммы называется зоной упрочнения. Здесь после стадии текучести материал снова приобретает способность увеличивать сопротивление дальнейшей деформации, однако для удлинения образца в этой зоне требуется в сотни раз более медленное нарастание нагрузки, чем в зоне упругих деформаций.
Точка С диаграммы характеризует максимальную (предельную) нагрузку Рmax и, соответственно, напряжения предела прочности или напряжения временного сопротивления σв, при которых еще сохраняется целостность элемента конструкции, нагруженного растяжением.
Дальше, за точкой С диаграммы, без увеличения внешней нагрузки идет лавинообразное разрушение межатомных связей материала.
Напряжение σв, таким образом, характеризует прочность материала на разрыв.
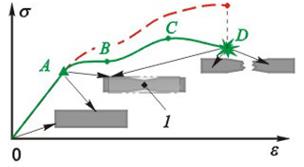
Точка D диаграммы характеризует разрушение (разрыв) образца. Нисходящая ветвь диаграммы С-D имеет условный характер, поскольку напряжения рассчитываются для площади поперечного сечения исходного образца. Реально напряжения растут, что
|
| Рис. 10.6. Диаграмма истинных напряжений |
показывает диаграмма истинных напряжений (рис. 10.6 - пунктирная линия), в которой напряжения рассчитываются для истинной площади поперечного сечения образца. В интервале О-А рост напряжения идет без разрушения межатомных связей, после снятия нагрузки образец возвращается к исходному состоянию. В интервале А-D рост напряжения происходит за счет разрушения межатомных связей и значительного местного утонения образца (образования шейки 1). В момент разрушения (точка D диаграммы) площадь поперечного сечения пластически деформированного образца меньше исходной.
Прочность конструкции, естественно, зависит от прочности материала, из которого она изготовлена.
Прочность (несущая способность) конструкции - это способность конструкции в определенных условиях воспринимать (выдерживать) без разрушения внешние нагрузки. Нагрузка, при которой происходит разрушение конструкции, называется разрушающей.
|
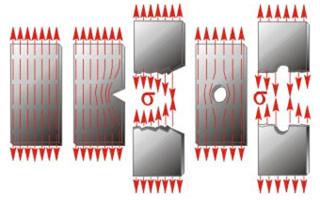
| Рис. 10.7. Траектории напряжений |
Несущая способность во многом зависит от пластичности материала. Пластичность - способность материала получать большие остаточные деформации, не разрушаясь. Хрупкость (свойство, противоположное пластичности) - способность материала разрушаться без заметной пластической деформации.
Жесткость - способность конструкции сопротивляться действию внешних нагрузок с допустимыми в эксплуатации деформациями, не нарушающими работоспособность конструкции.
Несущая способность конструкции резко снижается имеющимися в материале конструкции микротрещинами, вкраплениями инородных материалов, нарушающими постоянство напряжений.
Концентраторы напряжений - местные резкие изменения однородности (формы и, следовательно, жесткости) конструкции, приводящие к резкому местному (локальному) повышению напряжений в конструкции.
На рис. 10.7 показано действие растягивающей внешней нагрузки, равномерно распределенной по краям простейших конструктивных элементов - листов. Пунктирные линии представляют собой так называемые траектории напряжений, вдоль которых напряжение передается от молекулы к молекуле. Для гладкого листа эти линии параллельны, напряжения в любом сечении листа одинаковы.
Силы, передающиеся по траекториям напряжений в листах с концентраторами (надрез в кромке листа, отверстие в центре листа), обходят разрыв в материале. Плотность траекторий напряжений увеличивается, и локальные напряжения σ у края концентратора возрастают (иногда многократно). В этих местах может произойти нарушение (разрыв) межатомных связей, возникнут микротрещины, распространение которых ведет к разрушению конструкции.
|
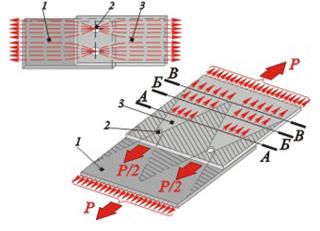
| Рис. 10.8. Передача нагрузки в соединении |
Распределение напряжений в законцовках (местах соединения деталей) обычно особенно сложно, в них обязательно появляются концентрации напряжений - местное повышение напряжений.
В месте соединения (рис. 10.8) листов 1 и 3 с помощью заклепок (или сварных точек) 2 передача нагрузки будет происходить только через точки крепления. Листы равномерно включатся в работу на достаточно большом удалении от места соединения.
Заштрихованная область листов практически выключена из работы и не испытывает напряжений. В то же время напряжения в поперечных сечениях листов распределены неравномерно, причем σА-А > σБ-Б > σВ-В.
Конструктор особое внимание должен уделять выбору формы деталей, работающих на растяжение, и особенно их законцовок, чтобы уменьшить возможные концентрации напряжений.
Сжатие
Механизмы разрушения (потери несущей способности) сжатых элементов существенно отличаются от механизмов разрушения растянутых элементов. При сжатии межатомные расстояния под нагрузкой уменьшаются, межатомные силы отталкивания растут, и конструкция стремится освободиться от запасенной энергии, переведя ее в работу "выскальзывания" атомов из-под нагрузки куда-либо в боковом направлении. В результате разрушение различных конструктивных элементов происходит по-разному, что определяется материалом конструкции и, главное, формой и пропорциями конструктивных элементов.
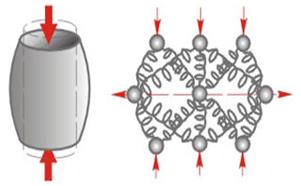
Короткие и "толстые" стержни (рис. 10.9) из пластичного материала при сжатии принимают бочкообразную форму ("сплющиваются"). Стержни из более упругого (хрупкого) материала (рис. 10.10) разрушаются с образованием трещины поперек стержня, и обе его части "проскальзывают" друг относительно друга.
| 
|
| Рис. 10.9. Упрощенная модель деформации при сжатии образца пластичного материала | Рис. 10.10. Упрощенная модель деформации при сжатии образца хрупкого материала |
Совершенно иначе теряют несущую способность при нагружении сжатием вдоль оси длинные и тонкие элементы конструкции, широко распространенные в самолетостроении.
При сжатии упругое тело (длинный стержень, тонкая пластина, панель и т. п.) сохраняет начальную (неизогнутую) форму равновесия до некоторого значения сжимающей силыРкр, называемой критической (или эйлеровой, так как Л. Эйлер был первым, кто предложил способ вычисления этой силы).
| 
|
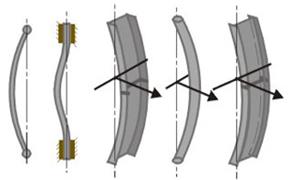
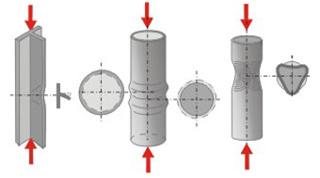
| Рис. 10.11. Oбщая потеря устойчивости стержнем | Рис. 10.12. Mестная потеря устойчивости тонкими стенками |
При небольшом превышении критической силы (и, соответственно, критических напряжений σкр) возникают значительные деформации стержня (см. рис. 10.11), который не разрушается, а только упруго изгибается и переходит к другой (изогнутой) форме упругого равновесия.
Если при этом не был достигнут "предел упругости", т. е. напряжения в стержне меньше напряжений предела пропорциональности, то при снятии нагрузки стержень возвращается в исходное состояние.
Л. Эйлер показал, что нагрузка, при которой стержень данной длины и площади поперечного сечения теряет устойчивость, не зависит от предела прочности материала, а зависит только от формы поперечного сечения, модуля упругости (жесткости) материала и условий закрепления концов стержня при нагружении.
При дальнейшем увеличении нагрузки изогнутый стержень разрушается. Такой вид потери несущей способности называется общей потерей устойчивости.
При отсутствии общей потери устойчивости (ось тонкостенного элемента конструкции прямолинейна, не деформирована) нагруженная сжатием конструкция может выйти из строя из-за местных деформаций отдельных участков. Такой вид (рис. 10.12) потери несущей способности называется местной потерей устойчивости.
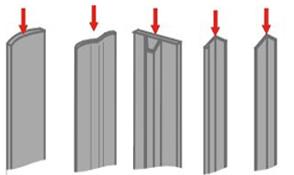
Эффективный способ повышения несущей способности тонкостенных конструкций при сжатии - придание им формы, увеличивающей критические напряжения общей потери устойчивости. Криволинейный и гофрированный листы (рис. 10.13) за счет изгибной жесткости (жесткости из плоскости листа, поперечной жесткости) обладают при сжатии большей несущей способностью, чем плоский лист, при одинаковой площади поперечного сечения. Профиль замкнутого сечения или профиль с местным утолщением - бульбом (от лат. bulbus - луковица) - эффективнее при сжатии, чем уголок.
| 
|
| Рис. 10.13. Различные формы стержней, работающих на сжатие | Рис. 10.14. Продольное подкрепление тонких стенок |
Увеличение несущей способности плоских или слабоизогнутых стенок обеспечивается подкреплением их в продольном (вдоль действия сжимающих сил) и в поперечном направлении ребрами жесткости (рис. 10.14). Такое подкрепление стенки обеспечивает ей высокие критические напряжения как общей, так и местной потери устойчивости.
Сдвиг
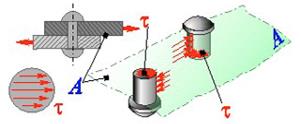
Примером сдвига (или среза) может служить (рис. 10.15) деформация в плоскости А заклепки, соединяющей два листа, нагруженные растяжением. При таком нагружении листы, как лезвия ножниц, стремятся перерезать заклепку. Напряжения сдвигаτ, возникающие на плоскости А в теле заклепки, называются касательными напряжениями.
| 
|
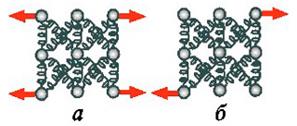
| Рис. 10.15. Сдвиг (срез) заклепки | Рис. 10.16. Упрощенная модель деформации при растяжении (а) и сдвиге (б) |
Сдвиг, таким образом, возникает, когда внешние силы смещают два параллельных плоских сечения элемента конструкции одно относительно другого при неизменном расстоянии между ними, и напряжения сдвига служат мерой сопротивления сдвигу (тенденции к скольжению) одной части твердого тела относительно другой.
Если при растяжении (или сжатии) (рис. 10.16,а) внешней нагрузке противостоят и прямые и диагональные межатомные связи, работающие на растяжение (сжатие), то при сдвиге (рис. 10.16,б) внешней нагрузке противостоят практически только диагональные связи, работающие на растяжение и сжатие. Поэтому напряжения сдвига, при которых происходит разрушение сдвигом, τв = (0,55 ¸ 0,65) σв.
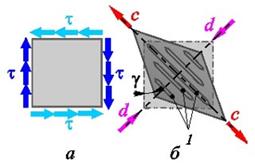
Нагружение тонкого листа (рис. 10.17,а) сдвигающими усилиями по вертикальным
|
| Рис. 10.17. Сдвиг тонкого листа |
кромкам требует для обеспечения статического равновесия соответствующих сдвиговых реакций по горизонтальным кромкам. Касательные напряжения по краям листа вызывают его деформацию (рис. 10.17,б). При этом вдоль диагонали с-с лист растягивается, а вдоль диагонали d-d сжимается. Следовательно, напряжения сдвига приводят к образованию напряжений растяжения и сжатия под углом ±45° к направлению сдвига.
В результате при достижении критических напряжений сдвига может произойти потеря устойчивости при сдвиге - гофрирование (от франц. gaufrer - прессовать складки) тонкого листа - образование гофра 1 поперек диагонали d-d.
Деформация чистого сдвига заключается в изменении прямых углов. Касательные напряжения τ связаны с угловыми деформациями γ соотношением
τ = Gγ,
| где | τ | - | касательное напряжение, Па; | |
| G | - | модуль сдвига (Па), зависящий от механических свойств материала и связанный через безразмерный коэффициент Пуассона µ с модулем упругости E соотношением G = E/2(1+µ); | ||
| γ | - | относительный сдвиг, определяющий искажение прямоугольного элемента (см. рис. 10.17). при сдвиге, который в силу малости угла γ можно принять равным отношению горизонтального сдвига нижней грани относительно верхней к расстоянию между этими гранями. |
Приведенные выше объяснения работы конструкции под нагрузкой имеют сугубо иллюстративный характер. В действительности механизмы разрушения значительно сложнее.
Причиной разрушения конструкции являются появляющиеся и развивающиеся в процессе эксплуатации трещины, возникновение которых наиболее полно объясняется представлением о дислокациях(от позднелат. dislokatio - смещение, перемещение) - несовершенствах (искажениях) атомно-кристаллических пространственных решеток реального металла конструкций, за счет движения, взаимодействия и развития которых (при приложении внешних нагрузок или под воздействием изменения температуры) возможен сдвиг кристаллических решеток вдоль действия силы.
Тем не менее модели деформации, проиллюстрированные рис. 10.3, 10.9, 10.10, 10.16, дают достаточно точное представление о характере разрушения при простейших случаях нагружения.
Кручение
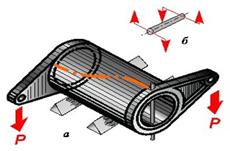
Схема нагружения кручением показана на рис. 10.18,б. Внешние силы, образующие момент относительно оси элемента конструкции, вызывают его деформации, которые заключаются в плоском повороте поперечных сечений друг относительно друга. Продольная линия, нанесенная на поверхность элемента конструкции, нагруженного кручением (рис. 10.18,а), принимает форму винтовой.
|
| Рис. 10.18. Нагружение кручением |
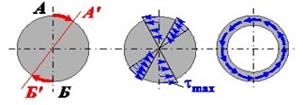
В любом поперечном сечении круглого стержня (рис. 10.19,а) при скручивании точка А на его поверхности стремится занять положение, отмеченное точкой А', а точка Б - положение Б'. Этому перемещению будут препятствовать внутренние силы - касательные напряжения (напряжения сдвига) τ, направленные вдоль кольцевых линий. Очевидно, что напряжения по сечению распределятся неравномерно (рис. 10.19,б). Они максимальны в крайних точках и снижаются до нуля на осевой линии. Несущая способность сплошного стержня используется не полностью (в центре материал недогружен).
Наиболее рациональным конструктивным элементом, предназначенным для восприятия кручения, является тонкостенная оболочка, по толщине которой (рис. 10.19,в) напряжения τ распределены практически равномерно.
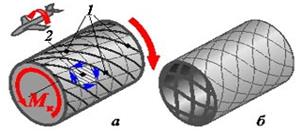
Однако нагружение кручением тонкостенной оболочки (рис. 10.20,а) может привести к потере устойчивости с образованием равномерно расположенных в окружном направлении вмятин, идущих от одного торца к другому по винтовым линиям 1.
| 
| ||
| Рис. 10.19. Напряжения при кручении | Рис. 10.20. Кручение тонкостенной оболочки | ||
| Сравните схему работы клетки 2 (заштрихованного элемента на рис.10.20,а) со схемой, изображенной на рис.10.17. | |||
Для повышения несущей способности такой оболочки ее необходимо подкреплять в направлении возможной потери устойчивости (подкрепление геодезического типа - рис. 10.20,б). Из технологических соображений подкрепление чаще ведется в продольном и поперечном направлениях (как на рис. 10.14), т. е. окантовывается клетка 2
(рис. 10.20,а), подверженная сдвигу при кручении.
Изгиб
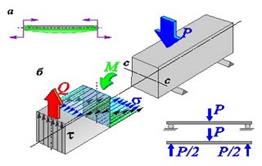
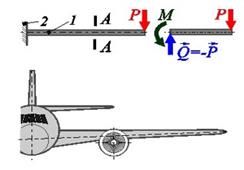
Схема нагружения изгибом показана на рис. 10.21,а. Внешние силы, образующие момент относительно оси с-с, перпендикулярной продольной оси балки, вызывают деформации, которые заключаются в искривлении продольной оси балки. Такой вид деформированного состояния называют чистым изгибом.
В технике широко распространен изгиб элементов конструкции, вызванный приложением к ним сосредоточенной силы или распределенной нагрузки (см. раздел 8.1, рис. 8.1-8.8).
| 
|
| Рис. 10.21. Изгиб балки прямоугольного сечения | Рис. 10.22. Уравновешивание балки при поперечной нагрузке |
Для простейшей балки прямоугольного сечения (рис. 10.21,б), нагруженнойсосредоточенной силой, деформированное состояние характеризуется наличием нормальных σ и касательных τ напряжений в любом поперечном сечении. Выпуклая сторона балки растянута, вогнутая - сжата. Зоны растяжения и сжатия разделены нейтральным слоем, длина которого при изгибе остается неизменной и нормальные напряжения в котором отсутствуют.
Статическое равновесие балки под поперечной нагрузкой обеспечивают нормальные напряжения σ, создающие уравновешивающий момент М, и касательные напряжения τ, создающие уравновешивающую перерезывающую силу Q. Это можно проследить, рассматривая равновесие по сечению А-А (рис. 10.22) консольной балки 1, заделанной на опору 2.
Как и в случае с кручением (см. рис. 10.19,в), сплошное поперечное сечение конструктивного элемента, работающего на изгиб, нерационально, так как вблизи нейтрального слоя материал недогружен.
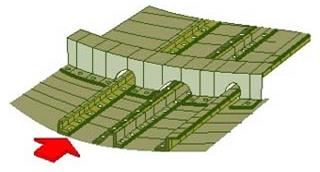
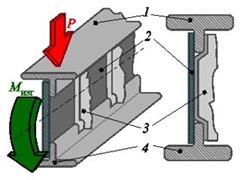
Наиболее рациональным будет сечение (рис. 10.23), в котором основная масса материала сосредоточена в зонах, максимально удаленных от нейтральной оси, - в поясах 1 и 4, которые, работая на растяжение (пояс 1) и сжатие (пояс 4), создают уравновешивающий изгибающиймомент Мизг. Тонкая стенка 2, соединяющая пояса и подкрепленная стойками 3, работая на сдвиг, создает уравновешивающую перерезывающую силу Р.
Различные внешние нагрузки, которые одновременно действуют на ЛА, стремясь деформировать и, в пределе, разрушить конструкцию, создают в ней весь спектр внутренних сил.
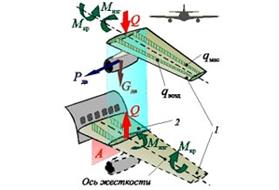
Так, (рис. 10.24) под действием распределенных воздушной qвозд и массовой qмас нагрузок и сосредоточенных сил тяги Рдв и веса Gдв двигателя в любом произвольно взятом сечении крыла (например, плоскостью А) возникнут внутренние силовые факторы: перерезывающая сила Q, изгибающий Мизг и крутящий Мкр моменты, которые будут уравновешивать условно отсеченную (концевую) часть крыла 1. Равные им, но противоположные по направлению силовые факторы для оставшейся (внутренней) части крыла 2 будут являться внешними нагрузками, заменяя отсеченную часть крыла.
| 
|
| Рис. 10.23. Тонкостенная балка | Рис. 10.24. Уравновешивание крыла |
В первом приближении можно не учитывать напряженно-деформированное состояние крыла под действием силы лобового сопротивления Х и силы тяги двигателя Рдв, стремящихся изогнуть конструкцию крыла в плоскости хорд, поскольку очевидно, что жесткость на изгиб крыла в этом направлении значительно больше, чем жесткость на изгиб "из плоскости" (в вертикальном направлении). Кроме того, силы, действующие на крыло в горизонтальной плоскости, значительно меньше.
Напомним, что в горизонтальном установившемся полете
Х = Y/К и Рдв = G/(Knдв) = Y/(Knдв),
| где | K | - | аэродинамическое качество самолета; | |
| nдв | - | число двигателей, в данном случае - два. |
Однако, как мы уже отмечали, при разработке конструкции ее работоспособность должна быть гарантирована для всех предусмотренных Нормами прочности случаев нагружения.
10.4. Подкрепленные тонкостенные оболочки - основа конструкции планера
Дата добавления: 2019-02-08; просмотров: 1478;











