Каноническая форма задачи ЛП

Для численного решения задачи ЛП требуется предварительно привести ее к каноническому виду:

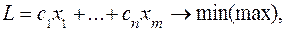
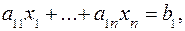(1)

………………………

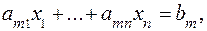
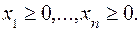
Каноническая форма (КФ) (1) задачи характеризуется следующими тремя признаками:

― однородная система ограничений в виде системы уравнений;

― однородные условия неотрицательности, распространяющиеся на все переменные, участвующие в задаче;

― минимизация (максимизация) целевой функции.

Известно, что для произвольной задачи ЛП можно построить эквивалентную ей каноническую задачу ЛП (эквивалентность двух задач означает, что оптимальному решению одной задачи соответствует оптимальное решение другой)[1,2,3].

Пример. Привести задачу к КФ на минимум:

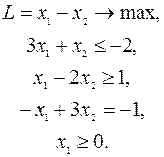(2)

В данной задаче (2) нарушены все три признака КФ.

1. Начнем с преобразования смешанной системы ограничений в систему уравнений. Для этого введем в первое и второе ограничения неотрицательные переменные y_1, y₂, которые называются дополнительными или слабыми. В результате система ограничений запишется в следующем виде:

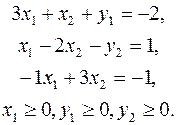(3)

2. Условия неотрицательности в (3) не выполняются только для переменной x₂. Для приведения задачи к однородным условиям неотрицательности можно воспользоваться двумя приемами.

Первый прием. Представим переменную x₂ в виде разности двух неотрицательных переменных: 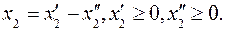После преобразования системы ограничений и целевой функции получим задачу

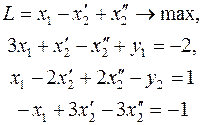(4)

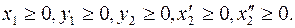
Второй прием. Найдем из какого-либо уравнения (4) переменную x₂. Пусть из первого уравнения 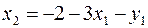. Подставим это выражение во все уравнения и в целевую функцию, исключив таким образом переменную x₂ из задачи. Получим

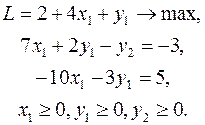(5)

3. Переход к задаче минимизации целевой функции L в задаче (5) осуществляется путем введения новой функции 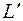из равенства

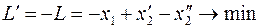в первом случае,

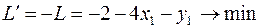во втором случае.