Kinematic Equations Derived from Calculus

Freely Falling Objects

Italian physicist and astronomer (1564–1642) Galileo formulated the laws that govern the motion of objects in free fall and made many other significant discoveries in physics and astronomy. Galileo publicly defended Nicolaus Copernicus’s assertion that the Sun is at the center of the Universe (the heliocentric system). He published Dialogue Concerning Two New World Systems to support the Copernican model, a view that the Catholic Church declared to be heretical.

The Italian Galileo Galilei (1564–1642) originated our present-day ideas concerning falling objects. There is a legend that he demonstrated the behavior of falling objects by observing that two different weights dropped simultaneously from the Leaning Tower of Pisa hit the ground at approximately the same time. Although there is some doubt that he carried out this particular experiment, it is well established that Galileo performed many experiments on objects moving on inclined planes. In his experiments, he rolled balls down a slight incline and measured the distances they covered in successive time intervals. The purpose of the incline was to reduce the acceleration, which made it possible for him to make accurate measurements of the time intervals. By gradually increasing the slope of the incline, he was finally able to draw conclusions about freely falling objects.

We shall denote the magnitude of the free-fall acceleration by the symbol g. The value of g decreases with increasing altitude above the Earth’s surface. Furthermore, slight variations in g occur with changes in latitude. At the Earth’s surface, the value of g is approximately 9.80 m/s². Unless stated otherwise, we shall use this value for g when performing calculations. For making quick estimates, use g = 10 m/s².

Kinematic Equations Derived from Calculus

The velocity of a particle moving in a straight line can be obtained if its position as a function of time is known. Mathematically, the velocity equals the derivative of the position with respect to time. It is also possible to find the position of a particle if its velocity is known as a function of time. In calculus, the procedure used to perform this task is referred to either as integration or as finding the antideriυatiυe. Graphically, it is equivalent to finding the area under a curve.

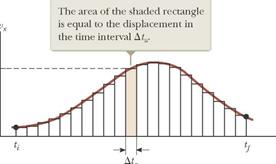
Suppose the υ_x–t graph for a particle moving along the x axis is as shown in Figure 1. Let us divide the time interval t_f - t_i into many small intervals, each of duration Δt_n. From the definition of average velocity, we see that the displacement of the particle during any small interval, such as the one shaded in Figure 1, is given by Δx_n = υ_xn,avg Δt_n, where υ_xn,avg is the average velocity in that interval. Therefore, the displacement during this small interval is simply the area of the shaded rectangle in Figure 1 The total displacement for the interval t_f – t_i is the sum of the areas of all the rectangles from t_i to t_f :

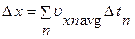
where the symbol ∑ (uppercase Greek sigma) signifies a sum over all terms, that is, over all values of n. Now, as the intervals are made smaller and smaller, the number of terms in the sum increases and the sum approaches a value equal to the area under the curve in the velocity – time graph. Therefore, in the limit n→ ∞, or Δt_n→0, the displacement is

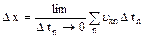(1)

The limit of the sum shown in Equation 1 is called a definite integraland is written

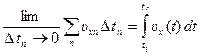(2)

Figure 1

where υ_x(t)denotes the velocity at any time t. If the explicit functional form of υ_x(t)is known and the limits are given, the integral can be evaluated.