Kinematic Equations

We now use the defining equations for acceleration and velocity to derive two of our kinematic equations:

υ_xf = υ_xi + a_xt (for constant a_x) (3)

and

x_f = x_i + υ_xi t+¹/₂a_xt²(for constant a_x) (4)

The defining equation for acceleration,

a_x=dυ_x/dt

may be written as dυ_x = a_x dt or, in terms of an integral (or antiderivative), as

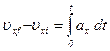
3. Summary(Lectures 1 – 3 )

Definitions

When a particle moves along the x axis from some initial position x_i to some final position x_f , its displacementis

Δx = x_f - x_i

The average velocityof a particle during some time interval is the displacement Δx divided by the time interval Δt during which that displacement occurs:

υ_x_,avg = Δx/Δt

The average speedof a particle is equal to the ratio of the total distance it travels to the total time interval during which it travels that distance

υ_avg = d/Δt

The instantaneous velocity of a particle is defined as the limit of the ratio Δx/Δt as Δt approaches zero. By definition, this limit equals the derivative of x with respect to t, or the time rate of change of the position:

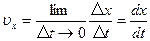
The average accelerationof a particle is defined as the ratio of the change in its velocity Δυ_x divided by the time interval Δt during which that change occurs:

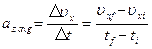
Дата добавления: 2016-07-18; просмотров: 1045;

Поиск по сайту

Узнать еще